Главная | Обратная связь

Геометричні ймовірності

Нехай на площині маємо деяку область G і в ній знаходиться друга область g. В область G навмання кидається точка, запитується, яка ймовірність, що ця точка попаде в область g ? Точка кидається навмання в область G означає, що ця точка може попасти в будь-яку точку області G, ймовірність попасти в якусь частину області G пропорційна виміру цієї частини(довжини, площі, об’єму) і не залежить від її роз положення.

Таким чином, по означенню, імовірність попадання в область при киданні навмання точки в область G рівна

.

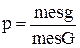Приклад. Задача про зустріч. Дві особи A і B домовились зустрітися в означеному місті між 12 і 13 годинами. Той, хто прийде першим, чекає другого протягом 20 хвилин, після чого покидає місце зустрічі. Чому дорівнює імовірність зустрічі осіб A і B, якщо прихід кожного із них на протязі вказаної години може здійснюватись навмання і моменти приходу незалежні.

Розв’язок. Позначимо момент приходу особи A через x і особи B через y. Для того, щоб зустріч відбулась, необхідно і достатньо, щоб . Зобразимо x і y як декартові координати на площині. За одиницю масштабу виберемо 1 хвилину. Можливі результати будуть зображені точками квадрата зі сторонами 60. Сприятливі зустрічі – розмістяться в заштрихованій області.

 

Шукана ймовірність

.

Приклад 2. Парадокс Бертрана. Навмання береться хорда в крузі. Чому дорівнює імовірність, що її довжина буде більша довжини сторони вписаного рівностороннього трикутника?

Розв’язок 1.З міркувань симетрії можна попередньо(заздалегідь) задати напрямок хорди. Проведемо діаметр, перпендикулярний до цього напрямку. Зрозуміло, що тільки хорди, які перетинають діаметр в проміжку від до його довжини, будуть більші сторони правильного трикутника.

AB=2BC=

Довжина сторони вписаного трикутника.

.

Таким чином, .

Розв’язок 2. З міркувань симетрії можна заздалегідь закріпити один із кінців хорди на колі. Дотична до кола в цій точці і дві сторони правильного трикутника з вершиною в цій точці утворюють пари кутів по . Умові задачі відповідають тільки хорди, які попадуть в середину кутів. Таким чином, .

Розв’язок 3. Щоб визначити положення хорди, достатньо задати її середину. Щоб хорда задовольняла умові задачі необхідно, щоб її середину знаходилась всередині круга, концентричного даному, але половинного радіуса. Площа цього круга дорівнює площі даного. .

.

У чому справа? Справа в тому, що за розв’язок однієї і тієї ж задачі, користуючись тим, що в умові задачі не визначено поняття проведення хорди навмання, видаються розв’язки трьох різних задач.

Дійсно, в першому розв’язку впродовж одного із діаметрів заставляють котитись круглий циліндричний стержень.

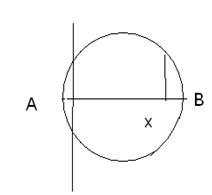
Множина всіх можливих місць зупинки цього стержня є множина точок відрізка AB довжини діаметра. Рівномірними вважаються події, що зупинка відбудеться в інтервалі довжини h, де б всередині діаметра, не був розміщений цей відрізок.

У другому розв’язку стержень, закріплений на шарніру, розташованому в одній із точок кола, заставляють здійснювати коливання розміром не більше . При цьому припускається, що зупинка стержня всередині дуги кола довжини h залежить тільки від довжини дуги, але не від її положення. Таким чином, рівномірними подіями вважаються зупинки стержня в будь-яких дугах кола однакової довжини.

Імовірність того, що стержень зупиниться в інтервалі від A до x, згідно першому розв’язку дорівнює . Імовірність того, що проекція точки перетину стержня з колом в другому розв’язку попаде в той же інтервал, як показують елементарні геометричні розрахунки, рівна

при ,

при .

У третьому розв’язку ми кидаємо навмання точку всередину круга і знаходимо імовірність попадання всередину деякого меншого концентричного круга.

Приклад 3. Задача Бюдхрона.

Площина розділена паралельними прямими, які знаходяться на відстані одна від другої 2a. На площину навмання кидається голка довжиною 2l( ). Знайти імовірність того, що голка перетне яку-небудь пряму.

Навмання: 1) центр голки навмання падає на відрізок довжини 2a, перпендикулярний до проведених прямих; 2) імовірність того, що кут φ, утворений голкою і проведеними прямими, буде заклечатись між і , пропорційна ; 3) величини x і φ незалежні.

Розв’язок. Позначимо через x – відстань від центра голки до найближчої паралелі і через φ – кут, утворений голкою і цією паралеллю. Величини x і φ повністю визначають положення голки. Можливі положення голки визначатимуться точками прямокутника зі сторонами a і π.

Із малюнка видно, що для перетину голки з паралеллю необхідно і достатньо, щоб . Шукана імовірність є відношення площі, заштрихованої до повної .

Одержана формула використовувалась для обчислення наближеного значення π.

Експериментатор	Рік	Число кидань голки	Експериментальне значення
Вольф			3,1596
Сміт			3,1553
Фокс			3,1419
Лаццарт			3,1415929

Так як із одержаної нами формули слідує рівність

.

При великому n

, де

m – число перетинів.

.