Главная | Обратная связь

Нерівність Чебишева

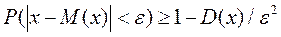
Доведення

Так як

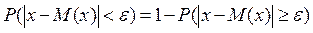
Відкинемо звідси ті доданки, для яких

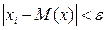
Будемо вважати, що це перші К доданків.

Тоді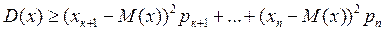

Так як або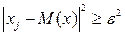

Тому 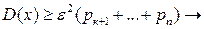ця сума є ймовірність того, що Х прийме одне із значень х_к+1,…,х_n, але для них . Звідки витікає, що сума 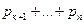є ймовірність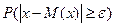

Тоді , або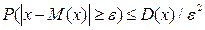

І, на кінець,

Доведено.

Нерівність Чебишева ( А.А.Боровков Теория вероятностей стр.94)

1-ша форма нерівності: Нехай ξ ≥ 0 з ймовірністю 1. Тоді для будь-якого ε >0

Р(ξ ≥ ε) ≤ 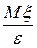(1)

2-га форма нерівності: Для будь-якої випадкової величини ξ, яка має скінченну дисперсію, при кожному ε >0 має місце нерівність

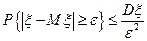(2)

Теорема Чебишева

Якщо ξ₁, ξ₂,…, ξ_n,… - послідовність попарно незалежних випадкових величин, які мають скінченні дисперсії, обмежені однією і тією ж сталою , то яке б не було постійне число ε >0

(3)

Доведення

В умовах теореми

,

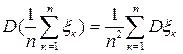так що

Згідно нерівності Чебишева

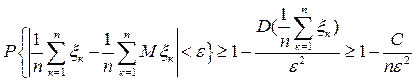
Переходячи до границі при , одержимо

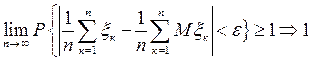
Теорема доведена.

 

Наслідки теореми Чебишева

Теорема Бернуллі

Нехай 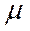- число появ події А в n незалежних випробуваннях і р є ймовірність появи події А в кожному із випробувань. Тоді, яке б не було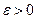

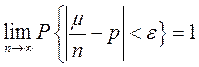(4)

Доведення

Дійсно, нехай 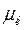- число появ події А в k-му випробуванні. Тоді

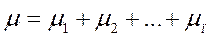
Але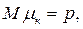

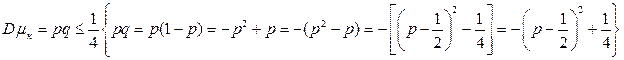
То теорема Бернуллі є найпростішим частинним випадком теореми Чебишева

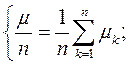
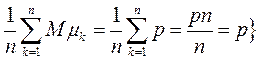
Теорема Пуассона

Якщо в послідовності незалежних випробувань ймовірність появи події А в k-му випробуванні дорівнює р_к, то

,

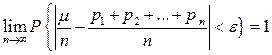де 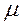- число появ події А в перших n випробуваннях.

Доведення

Вводячи в розгляд випадкові величини 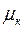, рівні числу появ події А в k-му випробуванні, і замітивши, що 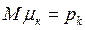, , ми переконуємось, що теорема Пуассона є частинним випадком теореми Чебишева.

3. Якщо послідовність попарно-незалежних випадкових величин 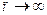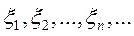так, що ,

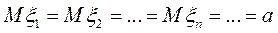то, яке б не було постійне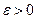

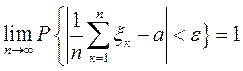
Цей наслідок використовується для середнього арифметичного. Нехай, наприклад, проводиться вимірювання n раз в однакових умовах деякої фізичної величини а.

Нехай х₁,х₂,…,х_n – результати вимірювань.

Тоді

Якщо вимірювання проводиться без систематичної похибки, тобто

,

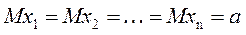то згідно закону великих чисел при 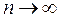з ймовірністю, як завгодно близькою до 1, ми можемо одержати значення, як завгодно близьке до а.