Главная | Обратная связь

Необхідна та достатня умова для закону великих чисел

Теорема

Для того, щоб для ймовірності 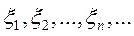(як завгодно залежних) випадкових величин при будь-якому 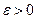виконувалось співвідношення

необхідно і достатньо, щоб при

Теорема Бореля

Нехай n – число появ події А при n незалежних випробуваннях, в кожному із яких подія А може з’явитися з імовірністю P. Тоді при

Доведення

Лема

Якщо при будь-якому цілому додатному r

то має місце ,

або

Нерідко із теореми Бернуллі роблять зовсім необґрунтований висновок, що частота події А при безмежному збільшенні числа випробувань прямує до імовірності події А. Насправді ж, теорема Бернуллі встановлює тільки той факт, що для достатньо великого числа випробувань n імовірність однієї єдиної нерівності 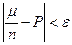становить більше ніж при довільному > 0

В 1909р французький математик Є. Борель знайшов більш глибоке твердження, яке одержало назву підсиленого закону великих чисел. Для цього введено поняття збіжності послідовності випадкових величин.

Нехай маємо послідовність випадкових величин, які визначені на одній і тій же множині елементарних подій U: (1)

Розглянемо точку А всіх елементарних подій е, для яких послідовність збігається. Нехай є в точці е.

Якщо через позначити множину тих е, для яких виконується нерівність

, (2)

то очевидно, що (3)

Дійсно, якщо послідовність функції збігається в точці е, то:

1) нерівності (2) повинні виконуватись для всіх к, якщо п достатньо велике;

2) вони повинні виконуватись, починаючи з деякого п;

3) вони повинні виконуватись при достатньо великих п для будь-якого значення .

Рівність 3) є символічним записом всіх цих вимог. Згідно рівності 3) і визначенню випадкової події, підмножина А належить полю випадкових подій. Визначимо випадкову величину наступним чином:

якщо , то ,

якщо ж , то .

Якщо ймовірність випадкових подій А рівна 1, то говорять, що послідовність випадкових величин збігається до випадкової величини з майже напевно (збігається з ймовірністю 1)

Поняття збіжності майже вірно в точності відповідає поняттю збіжності майже скрізь в теорії функцій. В теорії ймовірностей велику роль грає також збіжність за ймовірністю; послідовність випадкових величин збігається до випадкової величини 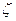за ймовірністю, якщо яке б не було 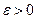, ймовірність нерівності

при прямує до 1.

Збіжність за ймовірністю є аналогом збіжності послідовності функцій за мірою, яка розглядається в теорії функцій.

Очевидно, що закон великих чисел стверджує, що при деяких умовах суми збігається за ймовірністю до нуля.

Якщо послідовність збігається до 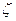майже вірно, то цей факт записують

(4)

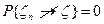або (4’)

Останнє означає, що ймовірність того, що знайдеться таке число r, що при всіх п і хоча б при одному значенні має місце нерівність дорівнює нулю.

Вкажемо одну із достатніх умов збіжності послідовності випадкових величин з ймовірністю одиниця. Лема.

Однак, не дивлячись на те, що , подія може здійснитись.

Властивість 3. Якщо можливі значення випадкової величини належать інтервалу , то:

1) при ;

2) при .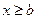

Наслідок. Якщо можливі значення неперервної випадкової величини міститься на всій вісі Ох, то

,