 |
|
Нерівність Чебишева
Нехай дано
| X | X1 | X2 | …. | Xn |
| P | P1 | P2 | …. | Pn |
Поставимо задачу оцінити ймовірність того, що відхилення випадкової величини від її математичного сподівання не перевищить 
абсолютний величини додатного числа 
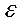достатньо малою.
Імовірність того ,що відхилення випадкової величини Х від її математичного сподівання по абсолютній величині менше додатного числа 
,не менше, ніж 
Доведення
Так як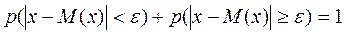 
звідси 
Віднімемо звідси ті доданки , для яких 
Будемо вважати що це перші К доданків
Тоді 
Так як 
або 
Тому 
Звідси витікає, що сума 
є імовірність
Тоді 
,
або 
.
І на кінець
Теорема Чебишева
Якщо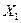 
, 
,…, 
– попарно незалежні випадкові величини, при тому дисперсія їх рівномірно обмежені , то яке б не було мале додатне число 
, імовірність нерівності
буде як завгодно близьким до 1 , якщо число випадкових величин достатньо велике
Тобто 
Доведення
Нехай 
тоді 
Використаємо для 
нерівність Чебишева
по умові 
і=1,2…n тому
тоді
але 
Наслідок:
Якщо 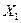, ,…, попарно незалежні випадкові величини , які мають одне і теж математичне сподівання А і якщо дисперсії цих величин рівномірно обмежені , то яке б не було мале число 
, імовірність нерівності
буде як завгодно близька до 1 , якщо число випадкових величин достатньо велике.
Тобто 
Теорема Чебишева говорить про те , що окремі випадкові величини можуть мати значний розсів , але їх середнє арифметичне розсіяне мало.
Таким чином, середнє арифметичне достатньо велике число незалежних випадкових величин (дисперсії яких рівномірно обмежені) визначають характер випадкової величини.
Пояснюється це тим, що відхилення кожної із величин від своїх математичних сподівань може бути як додатнім так і від’ємним , а в середньому арифметичному вони від’ємно компенсуються .
Теорема справедлива як для дискретних так і для незалежних випадкових величин .
Приклад використання теореми Чебишева
Розглянемо результати вимірювань деякої фізичної величини як випадкової величини , ,…,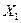
Результатами вимірювань є величина 
Тоді 
– попарно незалежні , мають одне і теж математичне сподівання , дисперсії їх рівномірно обмежені
Тоді по теоремі Чебишева
Тобто достатньо великих n середнє арифметичне вимірюваних величин дуже близьке істинного його значення
В статистиці теорема Чебишева дає можливість по невеликій вибірці робити істотні висновки про всю генеральну вибірку.