 |
|
Математичне сподівання, дисперсія функції
Часто на практиці немає необхідності знайти закон розподілу функції випадкової величини, а достатньо знайти деякі числові характеристики цієї функції.
Розглянемо тому задачу: випадкова величина Y є функція декількох випадкових величин Y = φ (Χ1,Χ2,…,Χn)
Відомий закон розподілу системи аргументів (Χ1,Χ2,…,Χn);необхідно знайти числові характеристики величини Y, в першу чергу – математичне сподівання та дисперсію.
Нехай ми знайшли закон розподілу g(γ) величини Y. Тоді

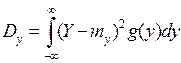 і т.д.
і т.д.
Проте закон g(γ) дуже важко знайти. Та для числових характеристик величини Y він не завжди потрібен, більше того, не завжди потрібен закон розподілу (Χ1,Χ2,…,Χn), достатньо знайти лише числові характеристики цієї системи. Розглянемо деякі випадки.
1. Задана випадкова величина Χ зі своїм законом розподілу і Y=φ(Χ)
Потрібно знайти my, не знаючи g(γ).
my=M(φ(χ)) (1)
Нехай Х – дискретна випадкова величина
| Χі | Χ1 | Χ2 | …. | Χn |
| Pі | Р1 | Р2 | …. | Рn |
| φ(Χі) | φ(Χ1) | φ(Χ2) | …. | Φ(Χn) |
| Pі | Р1 | Р2 | …. | Рn |
(2)
 (3)
(3)
Таким чином, для визначення математичного сподівання функції зовсім не вимагається знати закон розподілу цієї функції, а достатньо знайти закон розподілу аргумента.
Для неперервної величини:
 (4)
(4)
де f(x) – щільність розподілу випадкової величини X
 (5)
(5)
За аналогією
 (6)
(6)
 (7)
(7)
 (8)
(8)
Або
 (9)
(9)
 (10)
(10)
Теореми про числові характеристики
1. M(C)=0
2. D(C)=0
3. M(CX)=CM(x)
4. D(Cx)=C2D(X)
5. M(X+Y)=M(X)+M(Y)
6. 
7. D(X+Y)=D(X)+D(Y)+2Kxy
 Kxy=M(X0Y0)=M((X-mx)(Y-my))
Kxy=M(X0Y0)=M((X-mx)(Y-my))
коефіцієнт кореляції
Для некорельованих величин Kxy=0
8. 
9. 
10. 
Тут X та Y – незалежні випадкові величини.
Коефіцієнт кореляції лінійно залежних випадкових величин
Y=aX+b
Kxy=M(  )=M((X-mx)(Y-my))=M((X-mx)(aX+b-amx-b))=aM((X-mx)2)=a Dх
)=M((X-mx)(Y-my))=M((X-mx)(aX+b-amx-b))=aM((X-mx)2)=a Dх
rxy= 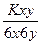
Dy=D(aX+b)=a2Dx
 y=|a|
y=|a| x
x
rxy= 
Доведемо, що rxy  1. Розглянемо
1. Розглянемо
в. в. Z=  yX
yX 
 xY
xY
Dz=  y2Dx
y2Dx 
 x2Dy
x2Dy  2
2  x
x  yKxy
yKxy 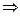
Dz=2  x2
x2  y2
y2  2
2  x
x  yKxy
yKxy 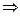
2  x2
x2  y2
y2  2
2  x
x  yKxy
yKxy  0 (так як Dz
0 (так як Dz  0)
0) 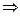
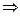
 x
x y
y  Kxy
Kxy  0|Kxy|
0|Kxy| 
 x
x  y
y 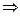
|rxy|  1.
1.