 |
|
Центральна гранична теорема для однаково розподілених доданків
Теорема. Якщо х1, х2, …, хn ,… – незалежні випадкові величини з одним і тим же законом розподілу (m,62), то при n  закон розподілу суми
закон розподілу суми
Уп=  (1)
(1)
необмежено наближається до нормального.
Доведення. Розглянемо х1,…, хn – неперервні випадкові величини. Характеристичне рівняння для хі
gx(t)=  (2)
(2)
gy(t)n=(gx(t))n (3)
згідно з попередніми теоремами.
Використаємо формулу Маклорена при t=0
gx (t) = gx (0)+ g’x (0)t+(  )t2,
)t2,
де  при
при 
Знайдемо  із (2) при t=0
із (2) при t=0
 (5)
(5)
Продиференціюємо (2)
 (6)
(6)
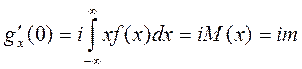 (7)
(7)
Не обмежуючи загальності , можна покласти m=0 (для цього достатньо перенести початок координат в точку m ).
Тоді 

 (8)
(8)
При m=0 інтеграл (8) є Dх
 (9)
(9)
Підставляючи в (4)  , одержимо
, одержимо
 (10)
(10)
Перейдемо від випадкової величини Уп до випадкової величини
 (11)
(11)
Ця величина зручна тим, що її дисперсія не залежить від п і дорівнює одиниці при будь-якому п. В цьому неважко переконатись, розглядаючи в.в. zn як лінійну функцію незалежним в.в. х2,…, хn кожна із яких має дисперсію 62. Якщо ми доведемо, що закон розподілу величини zn наближається до нормального, то очевидно, це буде справедливо і для величини уп , яка зведена з zn лінійною залежністю (11).
Замість того, що довести , що закон розподілу величини zn при  наближається до нормального б покажемо, що її характеристична функція наближається до хар-ної функції нормального закону. Хар. ф-ція zn
наближається до нормального б покажемо, що її характеристична функція наближається до хар-ної функції нормального закону. Хар. ф-ція zn
 із (11,8) (12)
із (11,8) (12)
Із (12) і (3)
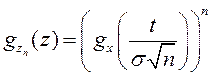 (13)
(13)
Із (10)
 (14)
(14)

Позначимо
 (15)
(15)
Тоді  (16)
(16)
При  (див. (15))
(див. (15))
 (один член розкладу взято)
(один член розкладу взято)
Тоді


По визначенню  при
при 
Звідси  і
і 
Звідси  (17)
(17)
Але це є характеристична функція нормального закону з
 .
.
Таким чином , при  характеристична функція
характеристична функція  до характеристичної функції нормального закону.
до характеристичної функції нормального закону.
Звідси впливає, що і закон розподілу zn (а значить і  )
)  до нормального закону. Доведено.
до нормального закону. Доведено.
Для неоднаково розподілених в.в. А.М. Лепунов довів центр. граничну теорему при умові:
 (18)
(18)
де  – третій абсолютний центральний момент величини
– третій абсолютний центральний момент величини  ,
,

Dк – дисперсія величини  .
.
Найбільш загальною (необхідною та достатньою) умовою справедливості центральної граничної теореми є умова Ліндерберга: при будь-якому  >0
>0

де  – математичне сподівання,
– математичне сподівання,
 – щільність розподілу випадкової величини
– щільність розподілу випадкової величини  ,
,
