 |
|
Елементи комбінаторики
Розміщення. Кінцеві впорядковані підмножини, що містять m елементів, узятих з n елементів основної множини, називаються розміщеннями з n елементів по m елементів. Число всіх можливих розміщень з n елементів по m позначають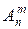 
.
(1.2)
Приклад. Нехай є три елементи А, В, С. Складемовсі комбінації з трьох елементів по два, отримаємо:
АВ, AC, ВА, ВС, СА, СВ.
Вони відрізняються або елементами, або їх порядком.
За формулою (1.2) маємо  .
|
Перестановки. Різні кінцеві впорядковані множини, що складаються зі всіх елементів деякої заданої множини називаються перестановками. Якщо основна множина містить n елементів, то число перестановок позначається 
. Перестановки – не що інше, як спосіб впорядкування якої-небудь кінцевої множини.
(1.3)
Приклад. Розглянемо три елементи: А, В, С. Складемовсі можливі комбінації з цих елементів:
АВС; АСВ; ВСА; ВАС; CAB; CBA (всього 6 комбінацій).
Видно, що вони відрізняються один від одного тільки порядком розташування.
За формулою (1.3) маємо  .
|
Сполучення. Кінцеві невпорядковані підмножини, які містять m різних елементів з n елементів заданої множини називаються сполученнями з n елементів по m.
Число сполучень з n елементів по m позначають 
. Воно дорівнює кількості способів, скількома можна витягувати m предметів з n можливих, якщо порядок ролі не грає, і обчислюється за формулою (0 £ m £ n):
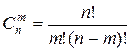(1.4)
Приклад. Розглянемо три елементи: А, В, С. Складемовсі можливі сполучення з трьох елементів по два: АВ, AC, ВС
За формулою (1.4)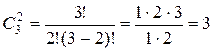 
|
Розміщення із повторенням. Беремо з множини навмання m елементів з поверненням. Тоді у фіксованій підмножині кожний елемент може повторитися m разів. Елементарною подією у випробуванні буде розміщення з n елементів по m із повторенням, а кількість таких розміщень
(1.5)
Приклад. Розглянемо три елементи А, В, С. Складемовсі комбінації з трьох елементів по два з повтореннями, отримаємо:
АВ, AC, ВА, ВС, СА, СВ, АА, ВВ, СС.
Вони відрізняються або елементами, або їх порядком.
За формулою (1.5)  , що співпадає з результатом приведеного прикладу.
|
Перестановки із повторенням. Маємо 
елементів, серед яких один елемент повторюється 
раз, інший елемент повторюється 
раз, і так далі, а останній елемент повторюється 
раз, причому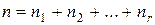 
. Число перестановок з повтореннями позначається 
та обчислюється за формулою
(1.6)
Приклад. Розглянемо елементи А, A, A, В, B. Складемовсі перестановки із повторенням, отримаємо:
АAABB, AABBA, ABBAA, BBAАА, BAAAB, ABAAB, AABAB, BABAA, BAABA, ABABA.
За формулою (1.6)  , що співпадає з результатом приведеного прикладу.
|
Сполучення з повтореннями. Якщо в сполученнях з n елементів по m деякі з елементів (і навіть всі) можуть виявитися однаковими, то такі поєднання називаються сполученнями з повтореннями із n елементів по m.
Число сполучень з повтореннями із n елементів по m позначається символом 
і обчислюється за формулою
. (1.7)
Приклад. Розглянемо три елементи А, В, С. Складемовсі сполучення з трьох елементів по два з повтореннями, отримаємо:
АВ, AC, ВС, АА, ВВ, СС.
За формулою (1.7)  , що співпадає з результатом приведеного прикладу.
|
| Приклад. У компанії 10 акціонерів, з них троє мають привілейовані акції. На збори акціонерів з'явилося 6 чоловік. Знайти ймовірність того, що з'явилися акціонери, які не мають привілейованих акцій. |
Розв’язання.
Позначимо 
= {серед шести чоловік немає жодного з привілейованими акціями}.
Випробуванням є відбір 6 чоловік з 10 акціонерів. Число всіх результатів випробування дорівнює числу сполучень з 10 по 6, тобто
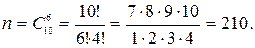
Результатом, що сприяє події А, є відбір шести чоловік серед семи акціонерів, які не мають привілейованих акцій. Число всіх результатів, що сприяють події А, буде 
Шукана ймовірність
.