Главная | Обратная связь

Раціональні дроби. Елементарні дроби. Розклад дробу на елементарні дроби надполями Q,R і C.

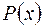Теорема 1. Для будь-якого поля існує єдине поле , яке містить кільце 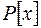многочленів над полем і кожен елемент якого можна подати у вигляді частки 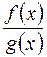, де .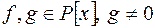

Означення 1.Раціональний дріб 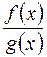називається правильним, якщо степінь многочлена менша за степінь многочлена . В іншому разі дріб – неправильний.

Приклад: - правильний дріб,
- неправильний дріб.

(Далі всі дроби вважати раціональними)

Лема 1. Сума правильних дробів є правильний дріб.

Означення 2. Елементарним дробом у полі Р називається раціональний дріб виду , де - незвідний многочлен у

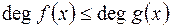полі , і , а 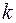– будь-яке натуральне число.

Кожен елементарний дріб є правильним.

 

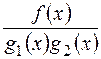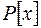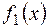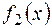Лема 2. Якщо і - взаємнопрості многочлени над полем Р і - правильний раціональний дріб над цим полем, то в кільці завжди можна знайти такі многочлени і , що .

Наслідок.Якщо 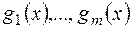- попарно взаємно прості многочлени над полем і 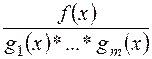- правильний раціональний дріб над цим полем, то в кільці 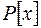завжди можна знайти такі многочлени , що 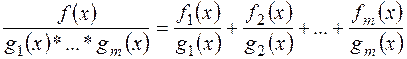, причому всі дроби у правій частині правильні.

Лема 3. Всякий правильний дріб над полем виду , де - многочлен, незвідний у полі Р, а 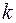- довільне натуральне число, можна подати як суму двох правильних дробів над полем виду 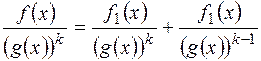, з яких перший є елементарний в полі .

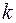Наслідок.Кожен правильний дріб над полем виду , де – многочлен незвідний у полі , а – довільне натуральне число, можна подати як суму елементарних дробів у цьому полі: .

 

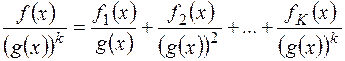Теорема 2.Всякий правильний дріб над полем можна подати як суму елементарних дробів у цьому полі.

Теорема 3.Розклад правильного раціонального дробу на елементарні дроби у даному полі єдиний.

Теорема 4.Всякий неправильний дріб 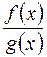над полем можна подати як суму многочлена і правильного дробу 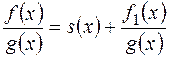, де 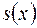- ціла частина дробу 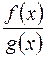, 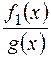– правильний дріб.

Нехай Р – деяке поле, 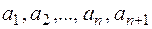- різні елементи поля і - довільні елементи поля . Існує один і тільки один многочлен в кільці Р[x], степінь якого не перевищує n і який набуває в (n + 1)-й точці 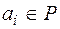задані значення ,

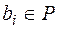Шуканий многочлен має вигляд

 

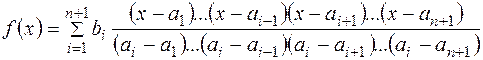(1)

 

Многочлен (1) називають інтерполяційним многочленом Лагранжа.

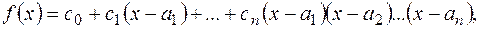Іноді доцільно многочлен записувати у вигляді (2)

 

(2)

де коефіцієнти 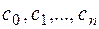визначаються послідовним підставленням значень .

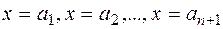Многочлен (2) називають інтерполяційним многочленом Ньютона.