 |
|
Кільце многочленів від n змінних. Розклад многочлена на добуток незвідних множників. Симетричні многочлени.
Означення 1.Кільцем многочленів  від
від  змінних
змінних  над областю цілісності R називається кільце многочленів від однієї змінної
над областю цілісності R називається кільце многочленів від однієї змінної 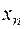 над кільцем
над кільцем  , тобто
, тобто  =
=  [
[ 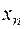 ].
].
Кільце многочленів  над областю цілісності R є область цілісності, причому кожен елемент
над областю цілісності R є область цілісності, причому кожен елемент  можна подати як скінчену суму:
можна подати як скінчену суму:  , (1),
, (1),
де 
Означення 2.Кожний елемент кільця  називається многочленом від
називається многочленом від  змінних над
змінних над 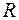 і позначається
і позначається  ,
, 
і т.д.
Кожен доданок  в сумі (1) називається членом многочлена
в сумі (1) називається членом многочлена  , елемент
, елемент 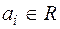 – коефіцієнтом цього члена. Два члени, які відрізняються тільки коефіцієнтами називаються подібними.
– коефіцієнтом цього члена. Два члени, які відрізняються тільки коефіцієнтами називаються подібними.
Приклад: -многочлен від двох зміннихx, y.
-многочлен від двох зміннихx, y.
Теорема 1.Будь-який многочлен  можна подати у канонічній формі ( без подібних членів ).
можна подати у канонічній формі ( без подібних членів ).
Означення 2Степенем члена  многочлена називається сума
многочлена називається сума  . Число
. Число  називається степенем даного члена відносно
називається степенем даного члена відносно  . Найбільший із степенів членів називається степенем многочлена, а член з найбільшим степенем – старшим членом многочлена.
. Найбільший із степенів членів називається степенем многочлена, а член з найбільшим степенем – старшим членом многочлена.
Приклад: 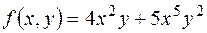
7 – степінь многочлена,  - старший член многочлена.
- старший член многочлена.
Означення 3.Якщо всі члени многочлена мають однаковий степінь, то многочлен називається однорідним.
Теорема 2.Якщо  і
і  – відмінні від нуля многочлени з
– відмінні від нуля многочлени з  , де
, де 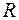 – область цілісності, то
– область цілісності, то  .
.
Нехай  і
і 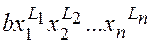 - два члени многочлена
- два члени многочлена  . Вважається, що перший елемент вищий від другого, якщо
. Вважається, що перший елемент вищий від другого, якщо  . Відношення “бути вищим” на множині членів многочленів є лінійним строгим порядком, його називають лексикографічним(позначають
. Відношення “бути вищим” на множині членів многочленів є лінійним строгим порядком, його називають лексикографічним(позначають 

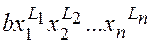 ).
).
Приклад:  - лексикографічний запис многочлена,
- лексикографічний запис многочлена,  - вищий член.
- вищий член.
Лема 1.Вищий член добутку двох многочленів дорівнює добутку вищих членів цих многочленів.
Означення 4. Вважатимемо, що многочлен  ділиться на многочлен
ділиться на многочлен 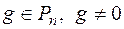 і записуватимемо
і записуватимемо 

 , якщо існує такий многочлен
, якщо існує такий многочлен  , що
, що  . При цьому
. При цьому  - дільник
- дільник  .
.
Властивості подільності:
1) 

2) 

3) 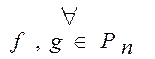

4) 




5) 

6) 

Означення 5. Многочлен  називається незвідним у
називається незвідним у
полі Р, якщо  і
і  .
.
Многочлен  називається звідним у полі Р, якщо
називається звідним у полі Р, якщо  і
і  .
.
Властивості незвідних многочленів:
1) Якщо р незвідний у полі  многочлен, то і будь-який асоційований з ним многочлен
многочлен, то і будь-який асоційований з ним многочлен  незвідний у полі
незвідний у полі  .
.
2) Якщо 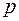 і
і  незвідні у полі Р многочлени і
незвідні у полі Р многочлени і 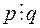 , то
, то 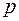 і
і  асоційовані.
асоційовані.
3) Будь-який многочлен  першого степеня незвідний у полі
першого степеня незвідний у полі  .
.
Теорема 3. Будь-який многочлен  над полем Р ненульового степеня множна подати як добуток многочленів, незвідних у полі Р, причому єдиним способом з точністю до сталих множників і їх порядку.
над полем Р ненульового степеня множна подати як добуток многочленів, незвідних у полі Р, причому єдиним способом з точністю до сталих множників і їх порядку.
Лема 2.Для будь-якої скінченої системи елементів  (
(  – область цілісності), відмінних від нуля, існує єдиний ( з точністю до дільників одиниці ) НСД.
– область цілісності), відмінних від нуля, існує єдиний ( з точністю до дільників одиниці ) НСД.
Означення 6.Многочлен  називається примітивним (відносно
називається примітивним (відносно  ), якщо НСД його коефіцієнтів дорівнює одиниці.
), якщо НСД його коефіцієнтів дорівнює одиниці.
Лема 3.Добуток двох примітивних многочленів з  є примітивний многочлен.
є примітивний многочлен.
Означення 7.Многочлен  називається симетричним відносно змінних
називається симетричним відносно змінних  , якщо внаслідок довільної перестановки змінних
, якщо внаслідок довільної перестановки змінних  утворюється многочлен рівний даному.
утворюється многочлен рівний даному.
Приклад: 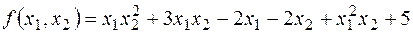 симетричний відносно
симетричний відносно  ;
;
 симетричний відносно
симетричний відносно  , але несиметричний відносно
, але несиметричний відносно  або
або 
 не симетричний відносно
не симетричний відносно 
Властивості симетричних многочленів:
1) Сума, різниця і добуток симетричних многочленів від n змінних над деяким полем  є симетричний многочлен над цим полем.
є симетричний многочлен над цим полем.
Наслідок. Множина всіх симетричних многочленів від  змінних над полем
змінних над полем  утворює область цілісності з 1 відносно дій додавання і множення.
утворює область цілісності з 1 відносно дій додавання і множення.
2) Якщо симетричний многочлен  містить деякий член
містить деякий член  , то він містить і член, утворений з даного, внаслідок будь-якої перестановки показників
, то він містить і член, утворений з даного, внаслідок будь-якої перестановки показників  .
.
3) Якщо  є вищий член симетричного многочлена, то
є вищий член симетричного многочлена, то  .
.
Теорема 4. (основна теорема теорії симетричних
многочленів)
Всякий симетричний многочлен  від
від  змінних над полем
змінних над полем  можна подати у вигляді многочлена від основних симетричних функцій
можна подати у вигляді многочлена від основних симетричних функцій  цих змінних, коефіцієнти якого належать тому ж полю
цих змінних, коефіцієнти якого належать тому ж полю  , причому це представлення єдине.
, причому це представлення єдине.
Елементарні симетричні многочлени:

Представлення симетричних сум через елементарні симетричні многочлени:



