 |
|
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ.
5.1.Упорядкувати лексикографічно і знайти вищий член многочлена  з кільця
з кільця  .
.
Розв’язання.
Маємо

Вищий член многочлена:  . Многочлен впорядковано за спаданням степенів
. Многочлен впорядковано за спаданням степенів  .
.
5.2.Застосовуючи заміну  розкласти на незвідні у полі
розкласти на незвідні у полі  многочлен
многочлен  .
.
Розв’язання.
Маємо:

 .
.
5.3. Чи симетричні многочлени:
 .
.
Розв’язання.
Нехай  , тоді
, тоді  ,
,
 цей многочлен несиметричний.
цей многочлен несиметричний.
 .
.
Розв’язання.
Нехай  , тоді
, тоді 
Нехай  , тоді
, тоді 
Нехай  , тоді
, тоді 
Цей многочлен симетричний.
5.4. Виразити через елементарні симетричні многочлени
 .
.
Розв’язання.

§ 6. Застосування симетричних многочленів до розв¢язування деяких задач з елементарної алгебри.
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ.
6.1. У множині дійсних чисел розв¢язати систему : 
Розв’язання.
Ліва частина кожного з рівнянь системи є симетричним многочленом. Так як
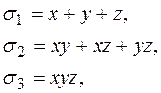
то з першого рівняння одержимо, що  .
.
Для другого рівняння маємо таке представлення:  Тому
Тому  = 9.
= 9.
Аналогічно для третього рівняння: 

 = 1.
= 1.
В результаті маємо систему:

За теоремою Вієта складемо відповідне рівняння  . Знайдемо його корені :
. Знайдемо його корені :
| -1 | -4 | |||
| -4 |


Повернувшись до змінних  , одержимо, що одним з розв¢язків даної системи рівнянь є
, одержимо, що одним з розв¢язків даної системи рівнянь є  = 1,
= 1,  = 2,
= 2,  = -2. Всі інші корені дістаємо перестановкою чисел 1, 2, -2.
= -2. Всі інші корені дістаємо перестановкою чисел 1, 2, -2.
Таким чином
(  ) є {(1, 2, -2),(1, -2, 2),(2, 1, -2),(-2, 1, 2),(2, -2, 1),(-2, 2, 1)}.
) є {(1, 2, -2),(1, -2, 2),(2, 1, -2),(-2, 1, 2),(2, -2, 1),(-2, 2, 1)}.
6.2.Розв¢язати систему ірраціональних рівнянь 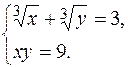
Розв’язання.
Зробимо заміну: 
Тоді матимемо систему рівнянь: 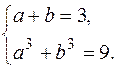
Позначимо:  і матимемо:
і матимемо: 
Повертаючись до змінних  і
і  , знаходимо:
, знаходимо:  .
.
Розв¢язками цієї системи є:  .
.
Враховуючи введену заміну, матимемо сукупність систем:

Розв¢язками системи є пари чисел : (1, 8) і (8, 1).
6.3.Скласти квадратне рівняння з коренями  і
і  , якщо
, якщо 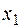 i
i  є коренями квадратного рівняння
є коренями квадратного рівняння  .
.
Розв’язання.
Коренями рівняння  є
є  відповідно
відповідно 
 Нове квадратне рівняння матиме вигляд:
Нове квадратне рівняння матиме вигляд: 
Складемо систему, підставивши замість  значення
значення 

Тому шукане квадратне рівняння має вигляд: 
6.4.Довести, що коли  +
+  +
+  = 0, то
= 0, то 
Розв’язання.
Виразимо  через елементарні симетричні многочлени:
через елементарні симетричні многочлени:
 .
.
Так як  , то
, то  .
.
Виразимо через елементарні симетричні многочлени вираз 

Матимемо, що 
Отже, рівність доведено.