Главная | Обратная связь

Дискримінант та результант двох многочленів, їх властивості і застосування до розв'язування задач.

 

Нехай і

- многочлени над полем , де і - корені .

 

Означення 1. Результантом многочленів і називається вираз виду

 

· Результант є симетричним многочленом від , тому результант довільних двох многочленів над полем є елементом цього поля.

 

Властивості результанта:

Нехай - корені многочлена . Тоді:

1) ,

2) .

 

Теорема 1. Для того, щоб і мали спільний корінь необхідно і достатньо, щоб їх результант дорівнював нулю.

 

При розв¢язуванні задач інколи важко знайти корені многочлена , тому результант ще можна подати у формі Сільвестра:

 

 

Теорема 2.Якщо =0, то і мають спільний корінь або обидва старші коефіцієнти дорівнюють 0.

Означення 2. Дискримінантом многочлена називається вираз виду ,

де - результант і його похідної .

 

· При цьому справджується рівність: ,

де корені .

 

Теорема 3. Многочлен має кратний корінь тоді і тільки тоді, коли його дискримінант рівний 0.

Нехай задано систему двох алгебраїчних рівнянь з двома невідомими, що мають коефіцієнти з поля Р:

 

Схема виключення невідомих з цієї системи:

1) упорядковуємо многочлени і за спадними степенями однієї із змінних, наприклад ;

2) складаємо результант , розглядаючи змінну як параметр;

3) знаходимо всі корені результанта: ;

4) підставляємо в задану систему замість змінної значення Þ дістаємо сукупність систем двох рівнянь з одним невідомим ;

5) розв'язуємо цю сукупність систем рівнянь і складаємо відповідні пари розв'язків.

 

 

ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ.

7.1.Обчислити результант для многочленів

 

Розв’язання.

І спосіб. Многочлен має коренями числа 3 і -1. Оскільки

 

то

 

ІІ спосіб. Нехай корені многочлена . Тоді

 

 

За теоремою Вієта, і . Тоді

 

 

Отже,

 

ІІІ спосіб. Обчислимо результант у формі Сільвестра :

 

 

 

7.2. При якому значенні мають спільні корені слідуючі многочлени .

Розв’язання.

Щоб многочлени мали спільні корені необхідно і достатньо, щоб їх результант був рівний нулю.

 

Запишемо результант у формі Сільвестра:

 

 

 

При многочлени і мають спільні корені.

 

7.3.При якому значенні має кратний корінь многочлен .

Розв’язання.

Необхідною і достатньою умовою, щоб многочлен мав кратний корінь є рівність нулю дискримінанта. Обчислимо його у формі Сільвестра:

 

 

 

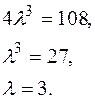
При цей многочлен має кратні корені.

 

7.4.Розв’язати систему рівнянь:

 

Розв’язання.

Розглянемо ліві частини кожного рівняння як многочлени від змінної

 

Розв¢язати систему рівнянь означає знайти спільні корені многочленів . Тому записуємо умову, при якій многочлени мають спільний корінь:

 

 

 

Підставляємо значення і у систему і одержуємо сукупність двох рівнянь з одним невідомим :

 

 

Розв’язуємо цю сукупність рівнянь і складаємо пари розв’язків: