 |
|
Рівняння третього степеня.
Нехай  - рівняння третього степеня з комплексними коефіцієнтами. За допомогою підстановки
- рівняння третього степеня з комплексними коефіцієнтами. За допомогою підстановки  зведемо його до виду
зведемо його до виду 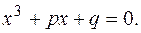 (1)
(1)
Число  називають дискримінантом рівняння (1).Корені цього рівняння знаходять за формулою
називають дискримінантом рівняння (1).Корені цього рівняння знаходять за формулою 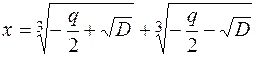 , яка називається формулою Кардано.
, яка називається формулою Кардано.
Якщо 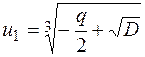 і
і 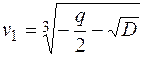 є тими значеннями кубічних коренів, при яких
є тими значеннями кубічних коренів, при яких  є коренями рівняння (1), то решту коренів цього рівняння обчислюють так:
є коренями рівняння (1), то решту коренів цього рівняння обчислюють так: 
Числа  знаходяться з умови
знаходяться з умови  .
.
Якщо коефіцієнти p i q рівняння (1) є дійсними числами, то:
1) при 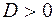 рівняння має один дійсний корінь і два комплексних спряжених корені;
рівняння має один дійсний корінь і два комплексних спряжених корені;
2) при  рівняння має три дійсних корені і два з яких дорівнюють один одному;
рівняння має три дійсних корені і два з яких дорівнюють один одному;
3) при 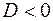 рівняння має три дійсних різних корені.
рівняння має три дійсних різних корені.
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ.
10.1.При яких дійсних значеннях  рівняння
рівняння  має один дійсний корінь і два комплексних корені.
має один дійсний корінь і два комплексних корені.
Розв’язання.
Щоб рівняння мало один дійсний корінь і два комплексних корені треба, щоб 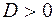 . Тому
. Тому
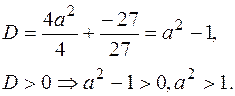
Тому такі корені будуть при 
10.2.Довести, що корені рівняння  є дійсними при будь-якому дійсному значенню числа
є дійсними при будь-якому дійсному значенню числа  .
.
Розв’язання.
Зведемо це рівняння до виду (1), ввівши заміну :  . Матимемо
. Матимемо
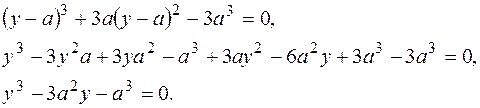
Щоб корені рівняння були дійсними при будь-якому дійсному значенню числа  треба, щоб виконувалася умова, що
треба, щоб виконувалася умова, що 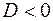 .
.
Дискримінант цього рівняння:
 < 0.
< 0.
Як бачимо умова виконується.
Отже рівняння має три різних дійсних корені при будь-якому дійсному значенню числа  , що і треба було довести.
, що і треба було довести.
10.3.Розв’язати рівняння: 
Розв’язання.
Дане рівняння є рівнянням виду (1), тому обчислюємо його дискримінант:
 .
.
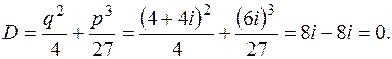
Тоді 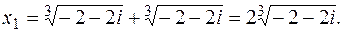
Далі 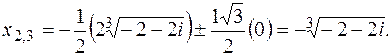
10.4.Розв’язати рівняння: 
Розв’язання.
Зведемо це рівняння до рівнянням виду (1), помноживши спершу обидві його частини на  :
:

Виконажмо заміну: 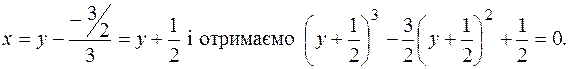
Маємо: 
Знаходимо дискримінант: 
Тоді 
§ 11. Відокремлення дійсних коренів многочленів.
Теорема Штурма.
1) Всі корені многочлена  лежать у середині круга з центром в точці 0 і радіусом
лежать у середині круга з центром в точці 0 і радіусом  .
.
2) Комплексні корені з дійсними коефіцієнтами розміщені симетрично відносно дійсної осі.
Теорема 1.Всі дійсні корені рівняння 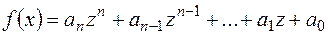 містяться в інтервалі
містяться в інтервалі  , де
, де  .
.
Одним з методів знаходження верхньої межі додатніх коренів многочлена з дійсними коефіцієнтами є метод Ньютона.
Теорема 2. Число М є верхньою межею додатніх коренів многочлена  , якщо при
, якщо при  = М многочлен
= М многочлен  має додатнє значення, а всі його похідні – невід’ємні значення.
має додатнє значення, а всі його похідні – невід’ємні значення.
Якщо 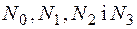 – верхні межі відповідно додатніх коренів многочлена з дійсними коефіцієнтами
– верхні межі відповідно додатніх коренів многочлена з дійсними коефіцієнтами  , то додатні корені многочлена
, то додатні корені многочлена  знаходяться у проміжку (
знаходяться у проміжку ( 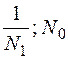 ), а від’ємні – у проміжку (
), а від’ємні – у проміжку (  ).
).
Означення 1.Нехай  - деяка впорядкована послідовність дійсних чисел. Кількість пар сусідніх чисел цієї послідовності, які мають протилежні знаки, називаєтьсякількістю змін знаків даної послідовності.
- деяка впорядкована послідовність дійсних чисел. Кількість пар сусідніх чисел цієї послідовності, які мають протилежні знаки, називаєтьсякількістю змін знаків даної послідовності.
Правило Декарта:
Число додатніх коренів многочлена з дійсними коефіцієнтами  дорівнює числу змін знаків у послідовності його коефіцієнтів або на парне число менше.
дорівнює числу змін знаків у послідовності його коефіцієнтів або на парне число менше.
Це правило можна застосувати і для оцінки кількості від’ємних коренів многочлена  за допомогою заміни
за допомогою заміни 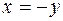 .
.
Щоб відокремити дійсні корені  необхідно знайти інтервали, у кожному з яких лежить лише один корінь. Це можна зробити методом Штурма.
необхідно знайти інтервали, у кожному з яких лежить лише один корінь. Це можна зробити методом Штурма.
Припускаємо, що  вже не має кратних коренів.
вже не має кратних коренів.
Спочатку будуємо ряд Штурма: 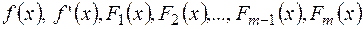 .
.
Щоб знайти многочлен  , застосуємо алгоритм, подібний алгоритму Евкліда:
, застосуємо алгоритм, подібний алгоритму Евкліда:
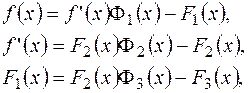
............................................
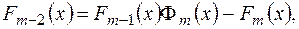
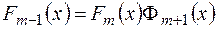 .
.
Для зручності позначимо:  . Тут всі остачі
. Тут всі остачі  беруться з протилежними знаками, тобто
беруться з протилежними знаками, тобто 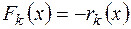 .
.
Властивості ряду Штурма:
Лема 1.Ніякі дві сусідні функції ряду не мають спільних коренів;
Лема 2.Якщо 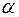 є коренем однієї з проміжних функцій ряду, то значення сусідніх з нею функцій ряду мають у цій точці протилежні знаки;
є коренем однієї з проміжних функцій ряду, то значення сусідніх з нею функцій ряду мають у цій точці протилежні знаки;
Лема 3.Якщо  , зростаючи, проходить через корінь якої-небудь проміжної функції ряду, але не проходить через корінь
, зростаючи, проходить через корінь якої-небудь проміжної функції ряду, але не проходить через корінь  , то число змін знаків у ряді Штурма при цьому не зміниться;
, то число змін знаків у ряді Штурма при цьому не зміниться;
Лема 4. Якщо  , зростаючи, проходить через корінь многочлена
, зростаючи, проходить через корінь многочлена  , то число змін знаків у ряді Штурма зменшиться на одиницю.
, то число змін знаків у ряді Штурма зменшиться на одиницю.
Теорема Штурма.
Якщо  і
і  (
( 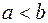 ) – довільні дійсні числа, які не є коренями
) – довільні дійсні числа, які не є коренями  , то число
, то число 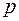 дійсних коренів многочлена
дійсних коренів многочлена  в інтервалі (
в інтервалі ( 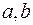 ) дорівнює
) дорівнює  , де
, де 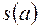 і
і 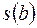 є число змін знаків у ряді Штурма відповідно у точках
є число змін знаків у ряді Штурма відповідно у точках  і
і  .
.
Застосування теореми Штурма:
1) для будь-якого многочлена  над полем дійсних чисел можна точно визначити загальне число дійсних коренів, а також число його додатніх і від’ємних коренів;
над полем дійсних чисел можна точно визначити загальне число дійсних коренів, а також число його додатніх і від’ємних коренів;
2) можна відокремити дійсні корені;
3) можна встановити,чи всі n коренів многочлена 
 -го степеня є різні дійсніі числа.
-го степеня є різні дійсніі числа.
Введемо такі позначення: М+-верхня межа додатніх коренів, m+ - нижня межа додатніх коренів, m_ - нижня межа від¢ємних коренів, M_ - верхня межа від¢ємних коренів.