 |
|
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ.
11.1.Знайти верхню межу додатніх коренів многочлена  методом Ньютона.
методом Ньютона.
Розв’язання.
Нехай 1 є верхньою межею додатніх коренів. Перевіримо, чи це дійсно так. Ділимо ліву частину на  за схемою Горнера і маємо:
за схемою Горнера і маємо:
| -8 | |||||
| -7 | -6 |
В нижньому рядку таблиці одержали від¢ємні числа, це означає, що число 1 не є верхньою межею додатніх коренів. Вже при М = 2 від’ємних коефіцієнтів в таблиці немає.
| -8 | |||||
| -7 | -6 |
Візьмемо число М = 1,9 < 2 і отримуємо в рядку від¢ємні числа.
| -8 | |||||
| 1.9 | 1.9 | 3.61 | -7 -1.141 | -6 -1.167 |
Тому можна взяти 2 в якості верхньої межі додатніх коренів: М+ = 2.
11.2.Знайти нижню межу додатніх коренів многочлена  методом Ньютона.
методом Ньютона.
Розв’язання. Для знаходження нижньої межі додатніх коренів зробимо заміну  і маємо рівняння
і маємо рівняння  .
.
За схемою Горнера ділимо на М = 1.3:

| -3 | ||||
| 1.3 | 1.3 | 2.69 | 0.5 | 5.6 |
При М = 1.3 від’ємних коефіцієнтів немає, але вже при М = 1,2 отримуємо в рядку від¢ємні числа:
| -3 | |||||
| 1.3 1.2 | 1.3 1.2 | 2.69 2.44 | 0.5 -0.56 | 5.6 4.32 |
Це значить, що за нижню межу додатніх коренів можна взяти 1.3: 
11.3.Знайти межі додатніх і від’ємних коренів многочлена  .
.
Розв’язання.
Якщо  – верхні межі відповідно додатніх коренів многочлена з дійсними коефіцієнтами
– верхні межі відповідно додатніх коренів многочлена з дійсними коефіцієнтами  , то додатні корені многочлена
, то додатні корені многочлена  знаходяться у проміжку (
знаходяться у проміжку ( 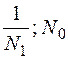 ), а від’ємні відповідно у проміжку (
), а від’ємні відповідно у проміжку (  ).
).
Знайдемо спочатку верхню межу додатніх коренів за формулою  .
.
Тут  . Отже
. Отже  . Але це занадто велике число. Перевіримо за теоремою Ньютона, чи не буде верхньою межею, наприклад, число 4. Для цього, користуючись схемою Горнера, знайдемо значення всіх похідних від
. Але це занадто велике число. Перевіримо за теоремою Ньютона, чи не буде верхньою межею, наприклад, число 4. Для цього, користуючись схемою Горнера, знайдемо значення всіх похідних від  при
при  , причому нас цікавлять не самі значення похідних, а їх знаки:
, причому нас цікавлять не самі значення похідних, а їх знаки:
| -3 | -25 | -41 | -18 | |||
| + |
(замість остачі поставимо знак +, бо видно, що вона додатня).
Оскільки коефіцієнти за схемою Горнера будуються за допомогою тільки додаванняі множення, а вдругому рядку цієї схеми стоять лише додатні числа, то при наступних діленнях від’ємні коефіцієнти з’явитись не можуть.
А тому всі остачі, отже і похідні від  будуть додатні. Число 4 теж є верхня межа додатніх коренів
будуть додатні. Число 4 теж є верхня межа додатніх коренів  . Але ми шукаємо таку цілочисельну верхню межу
. Але ми шукаємо таку цілочисельну верхню межу  , що
, що  вже не задовольняє умову теореми Ньютона.
вже не задовольняє умову теореми Ньютона.
Перевіримо, чи не буде верхнею межею число 2. Складемо схему Горнера для  :
:
| -3 | -25 | -41 | -18 | |||||||||||
| -11 | -63 | - | ||||||||||||
Із схеми видно, що  . Число 2 не є верхня межа коренів. Перевіримо ще число 3:
. Число 2 не є верхня межа коренів. Перевіримо ще число 3:
| -3 | -25 | -41 | -18 | |||
| + |
З наведених вище міркувань робимо висновок, що число 3 задовольняє умові теореми Ньютона, а тому і є верхня межа додатніх коренів  . Причому 3 є найменша з цілочисельних верхніх меж, бо 2 вже не є верхня межа.
. Причому 3 є найменша з цілочисельних верхніх меж, бо 2 вже не є верхня межа.
Отже  = 3.
= 3.
Для знаходження нижньої межі від’ємних коренів  розглянемо многочлен
розглянемо многочлен  .
.
Знайдемо межу:  . Але знову ж це занадто велике число. Перевіримо за теоремою Ньютона, чи не буде верхньою межею многочлена
. Але знову ж це занадто велике число. Перевіримо за теоремою Ньютона, чи не буде верхньою межею многочлена  , наприклад, число 3:
, наприклад, число 3:
| -3 | -3 | -41 | ||||
| -3 | + | |||||
| + | + |
Знову одержали рядок із додатніх чисел. При наступних діленнях всі числа так само будуть додатні, а тому 3 є верхня межа. Перевіримо, чи не буде верхньою межею число 2:
| -3 | -3 | -41 | ||||
| -1 | -5 | -11 | -4 |
Щскільки  , то число 2 не є верхня межа додатніх коренів многочлена
, то число 2 не є верхня межа додатніх коренів многочлена  :
:
 .
.
Число -3 є нижня межа від’ємних коренів многочлена  .
.
Аналогічно знаходимо верхні межі додатніх коренів для многочленів

Це будуть відповідно  , а тому нижня межа додатніх коренів многочлена
, а тому нижня межа додатніх коренів многочлена  буде
буде 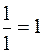 , верхня межа від’ємних коренів буде
, верхня межа від’ємних коренів буде  .
.
Таким чином, додатні корені многочлена  розташовані між числами 1 і 3, від’ємні корені – між числами -3 і
розташовані між числами 1 і 3, від’ємні корені – між числами -3 і  .
.
11.4. Знайти число дійсних коренів для многочлена  на проміжку [2,4].
на проміжку [2,4].
Розв’язання.
Побудуємо ряд Штурма.
 ,
,
то в якості 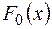 можна взяти
можна взяти  .
.
Ділимо  на
на  :
:
x4 - 2x3 - 6x2 + 4x + 4 | 2x3 - 3x2 – 6x + 2
_ 2x4 - 4x3 - 12x2 + 8x + 8 | x - 1
2x4 - 3x3 - 6x2 + 2x
x3 - 6x2 + 6x + 8
_ 2x3 - 12x2 + 12x + 16
2x3 - 12x2 + 12x + 16
-15x2 + 6x + 18
Остача  . Тому
. Тому  .
.
Далі ділимо 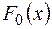 на
на  :
:
2x3 - 3x2 – 6x + 2 | 5x2 - 2x - 6
_ 10x3 - 15x2 – 30x + 10 | 2x - 11
10x3 - 4x2 – 12x
- 11x2 – 18x + 10
_ - 55x2 – 90x + 50
- 55x2 – 90x + 50
–112x - 16 
Далі ділимо  на
на 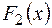 :
:
5x2 - 2x - 6 | 7x + 1
_ 35x2 - 14x - 42 | 5x - 19
35x2 - 14x
-19x - 42
_ -133x -294
-133x - 19
-275 Þ 
Тоді остаточно маємо

Побудуємо таблицю

| 
| 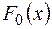
| 
| 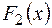
| 
| 
|
| - | - | + | + | + | ||
| + | + | + | + | + |
 - одна зміна знаку,
- одна зміна знаку,  - змін знаку немає.
- змін знаку немає.
При зростанні  від 2 до 4 число кількості змін знаків в ряді Штурма:
від 2 до 4 число кількості змін знаків в ряді Штурма:  , тобто на проміжку [2,4] знаходиться один дійсний корінь.
, тобто на проміжку [2,4] знаходиться один дійсний корінь.
11.5. Відокремити дійсні корені многочлена 
Розв’язання.
Дійсні корені лежать в інтервалі  , де
, де  . В даному випадку
. В даному випадку  , тому розглядаємо інтервал (-3, 3).
, тому розглядаємо інтервал (-3, 3).
Побудуємо ряд Штурма.
 , то в якості
, то в якості 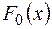 можна взяти
можна взяти 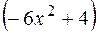 .
.
Ділимо  на
на  :
:
-8x + 16x – 2 |-6x2 + 4
_ -24x + 48x – 6 | 4x
-24x + 16x
32x – 6 Þ 
Далі ділимо 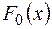 на
на  :
:
-6x2 + 4 | -16x + 3
_ -48x2 + 32 | 3x
-48x2 + 9
23 

Для  маємо
маємо  .
.
Складемо таблицю:

| 
| 
| 
| 
| 
|
| -3 | + | - | + | - | |
| -2 | + | - | + | - | |
| -1 | - | - | + | - | |
| - | + | + | - | ||
| + | - | - | - | ||
| - | - | - | - | ||
| - | - | - | - |
З таблиці видно, що один корінь лежить в інтервалі (-2;-1), бо  , другий корінь знаходиться в інтервалі (0;1), бо
, другий корінь знаходиться в інтервалі (0;1), бо  , а третій – в інтервалі (1;2), бо
, а третій – в інтервалі (1;2), бо  .
.