Главная | Обратная связь

Теорема 14,15 (критерий Коши сходимости последовательности).

Теорема 1,2.

Определения предела функции в точке a по Гейне и по Коши эквивалентны.

Доказательство. Пусть f(x) = b по Коши. (1) Требуется доказать, что " {x_n} ® a (x_n ¹ a) соответствующая последовательность {f(x_n)} ® b, то есть " e > 0 $ N, " n > N: ½f(x_n) - b½ < e. (2) Рассмотрим произвольную последовательность {x_n} ® a (x_n ¹ a). Возьмем e > 0. В силу условия (1) $ d > 0, " x Î {0 <½x - a½ < d}: ½f(x) - b½ < e. (3) В свою очередь, так как {x_n} ® a (x_n ¹ a),

то для указанного d $ N, " n > N: 0 <½x_n - a½ < d (4). Из (4) и (3) следует, что " n > N: ½f(x_n) - b½ < e, то есть выполнено условие (2), что и требовалось доказать. Пусть f(x) = b по Гейне. (5) Предположим, что f(x) ¹ b по Коши.

Тогда $ e > 0 такое, что " d > 0 $ xÎ {0 <½x - a½< d}: ½f(x) - b½³ e. Возьмем какую-нибудь последовательность {d_n} ® +0 (d_n > 0). Например, можно взять d_n = 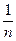. Согласно сказанному выше, " d_n $ x_n Î : ½f(x_n) - b½³ e. (7) Из (6) следует, что {x_n} ® a (x_n ¹ a). Отсюда в силу условия (5) следует, что {f(x_n)} ® b, и поэтому = 0. С другой стороны, в силу неравенства (7) ³ e > 0. Полученное противоречие доказывает, что наше предположение неверно и, следовательно, f(x) = b по Коши. Теорема доказана.

Теорема 7,8.

Любая ограниченная последовательность имеет верхний и нижний пределы.

Доказательство. Пусть {x_n} - ограниченная последовательность. Обозначим через {a} множество всех предельных точек этой последовательности. Так как это множество ограничено и непустое, то оно имеет точные грани. Обозначим = Sup {a}, = inf {a}. Достаточно доказать, что Î {a}, Î {a}. Проведем доказательство для . Рассмотрим произвольную e-окрестность точки и, кроме того, рассмотрим -окрестность точки . По определению точной верхней грани, существует точка a Î {a}: a Î { -окрестности точки a}, а по определению 2 предельной точки в -окрестности точки a содержится бесконечно много членов последовательности {x_n}. Но { -окрестность точки a} Ì {e-окрестности точки }, тем самым, в e-окрестности точки содержится бесконечно много членов последовательности {x_n}, а это и означает, что - предельная точка последовательности {x_n}, то есть Î {a}. теорема доказана.

Теорема 10.

Пусть f(x)- монотонная и ограниченная на полупрямой (а, + ¥), тогда существует f(x).

Доказательство: Пусть, для определённости f(x) не убывает и ограничена сверху на (а, + ¥). Тогда она имеет на (а, + ¥) точную верхнюю грань. Введём обозначение: f(x) = b. Докажем, что f(x) = b. Зададим произвольное e > 0 и рассмотрим число b - e < b, по определению точной верхней грани $ А: f(A) > b - e. Так как f(x) ³ f(a) при x ³ A, то f(x) > b - e при x ³ A, или b - f(x) < e при x ³ A, то есть | f(x) - b | < e при x ³ A. а это и означает, что f(x) = b. Теорема доказана.

Теорема 13.

Фундаментальная последовательность ограничена.

Доказательство. Пусть {x_n} - фундаментальная последовательность. Возьмем какое-нибудь положительное e, например, e = 1. По определению фундаментальности, $ N, " n >N и " m > N:½x_m-x_n½ < 1. Зафиксируем какое-нибудь m₀ > N, тогда < 1 при n >N, или - 1 < x_n < + 1 при n >N. Таким образом, все члены последовательности с номерами n >N лежат в интервале - 1, + 1), вне этого интервала лежит только конечное число членов последовательности. Это и означает, что последовательность {x_n} ограничена. Теорема доказана.

Теорема 14,15 (критерий Коши сходимости последовательности).

Для того, чтобы числовая последовательность сходилась, необходимо и достаточно, чтобы она была фундаментальной.

Доказательство. Необходимость. Последовательность {x_n} сходится. Требуется доказать, что последовательность {x_n} - фундаментальная. Пусть =a. Зададим произвольное e > 0. По определению предела, $ N, " n > N:½x_n-a½ < , и " m > N:½x_m-a½ < . Если n > N, m > N, то ½x_m-x_n½=½(x_m-a) - (x_n-a)½£ + < e. Это и означает по определению, что последовательность {x_n} - фундаментальная. Необходимость доказана.

Достаточность. Последовательность {x_n} - фундаментальная. Требуется доказать: {x_n} сходится. По лемме 2, последовательность {x_n} ограничена, следовательно, можно выделить сходящуюся подпоследовательность . Пусть = a. Докажем, что = a. Зададим произвольное e > 0. Так как подпоследовательность сходится к a, начиная с некоторого номера N₁ все члены Î { - окрестности точки a}, а так как последовательность {x_n} - фундаментальная, то начиная с некоторого номера N₂ все члены x_n отстоят от членов меньше, чем на . Следовательно, начиная с номера N = max (N₁, N₂) все члены последовательности x_n Î {e- окрестности точки a}, а это и означает, что = a, что и требовалось доказать. Теорема доказана.