 |
|
Розв’язання задач теорії пружності в переміщеннях
Для визначення трьох невідомих складові переміщення 
необхідно мати три рівняння, які можна одержати з диференціальних рівнянь рівноваги (2.1), виразивши в них напруги через переміщення. Скористаємося першим рівнянням (2.1) і підставимо в нього напруги з формул закону Гука (2.6):
Підставивши в це рівняння значення деформацій (2.3), після групування доданків знаходимо
| (2.7) |
Вирази в перших дужках можна позначити скорочено:
| (2.8) |
Цей диференціальний оператор називається оператором Лапласа над функцією 
й читається «набла два 
».
Вираз, що знаходиться в других дужках, можна спростити в такий спосіб:
Після зазначених скорочень і спрощень рівняння (2.7) приймає вигляд
Аналогічно перетворимо й два інших диференціальних рівняння рівноваги (2.1). Таким чином, одержуємо систему рівнянь для розв’язання задач теорії пружності в переміщеннях:
| (2.9) |
Ці рівняння називаються рівняннями Ламі. Вони поєднують статичні, геометричні й фізичні передумови теорії пружності, розглянуті вище. Дійсно, в них знаходяться умови рівноваги кожного елемента тіла, геометричні характеристики деформації 
й фізичні характеристики матеріалу 
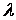й 
.
Так само як і рівняння рівноваги, перетворимо умови на поверхні. Для цього в перше рівняння (2.2) підставимо вираз напруг через деформації (2.6):
| (2.10) |
Вираз в перших дужках являє собою похідну функції по напрямку нормалі до поверхні тіла. Дійсно, обчислюючи частинну похідну складної функції по змінній , одержуємо
Похідні координат по являють собою відповідні напрямні косинуси нормалі :
Таким чином,
і рівняння (2.10) приймає вигляд
| (2.11) |
Точно так само можна перетворити два інших рівняння (2.2).У результаті приходимо до наступних трьох умов на поверхні, виражених через переміщення:
| (2.12) |
Тепер можна скласти план безпосереднього розв’язання задач теорії пружності в переміщеннях. Для визначення трьох складових переміщення 
необхідно про інтегрувати три рівняння Ламе (2.9) і задовольнити умовам на поверхні (2.12). По знайдених переміщеннях з геометричних співвідношень Коші (2.3) визначають складові деформації, а потім з формул закону Гука (2.6) - складових напруг.