Главная | Обратная связь

Методи рішення плоскої задачі для прямокутних однозв'язних областей

Відшукання бігармонічної функції, що задовольняє умові на контурі прямокутної області, можливо різними методами. Обмежимося розглядом лише деяких з них: рішенням плоского задачі в поліномах (цілих функціях), у тригонометричних рядах, за допомогою кінцевих різниць.

1. Рішення в поліномах. Рішення плоскої задачі можна здійснити напівзворотнім методом, якщо спочатку задатися аналітичною формою функції напружень, що задовольняє бігармонічному рівнянню (3.11), а потім визначити, яким навантаженням на контурі вона відповідає. У якості бігармонічної функції можна прийняти алгебраїчні поліноми різних ступенів.

Поліном першого ступеня як функція напружень нас не цікавить, тому що напруження, підраховані по формулі (3.10), виявляться рівними нулю.

Розглянемо функцію напружень у вигляді полінома другого ступеня

(3.12а)

Четверті похідні цієї функції:

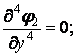
і, отже, рівняння (3.11) обертається в тотожність при будь-яких значеннях коефіцієнтів , , . Таким чином, поліном другого ступеня є бігармонічною функцією й може бути застосований до рішення плоскої задачі.

Якщо функцію напружень прийняти у вигляді полінома третього ступеня

(3.13)

то рівняння (3.11) як і раніше буде звертатися в тотожність при довільних значеннях коефіцієнтів 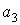, , 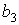і , тобто поліном третього ступеня є бігармонічною функцією і також може бути застосований для рішення плоскої задачі.

Задамо функцію у вигляді полінома четвертого ступеня:

(3.14)

Четверті похідні цієї функції:

Підставляючи їх у бігармонічне рівняння (3.11), одержуємо

звідки

(a)

Таким чином, не всі коефіцієнти полінома четвертого ступеня довільні. Незалежними можуть бути тільки чотири коефіцієнти, наприклад 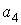, , і , a п'ятий варто взяти зі співвідношення (а). Отже, для того щоб поліном четвертого ступеня був бігармонічної функцією, він повинен мати такий вид:

Розглянемо поліном п'ятого ступеня:

(3.15)

Четверті похідні цієї функції:

Підставляючи їх у бігармонічне рівняння (3.11) і групуючи доданки по аргументах і 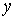, одержуємо

.

Щоб це рівняння оберталося в тотожність при будь-яких значеннях аргументів, необхідно коефіцієнти при цих змінних дорівняти нулю:

(б)

Якщо незалежними прийняти коефіцієнти , , і , то інші два виразяться через них відповідно до рівнянь (б) у
такий спосіб:

(в)

Вносячи коефіцієнти й зі співвідношень (в) у формулу (3.15), знаходимо

(3.16)

У такій формі поліном п'ятого ступеня є бігармонічною функцією і його можна застосувати до рішення плоскої задачі.

За допомогою алгебраїчних поліномів можна вирішити, ряд простих задач: задача про чистий згин балки, згинанні балки на двох опорах під дією рівномірно розподіленого навантаження, задача про трикутну підпірну стінку.

2. Метод тригонометричних рядів Рібьєра-Файлона. Як функція напружень можна застосовувати тригонометричні ряди. Досліджуємо із цією метою тригонометричну функцію

де Y - функція, що залежить тільки від координати в;

(г)

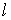— будь-яке ціле число; — довжина пластинки в напрямку осі . З'ясуємо, при яких умовах функція є бігармонічною, тобто, задовольняє рівнянню (3.11). Підрахуємо четверті похідні функції :

Підставляючи їх у зазначене рівняння, одержуємо

або

Це рівняння обертається в тотожність при будь-яких значеннях аргументу , якщо задовольняє диференціальному рівнянню

рішення якого можна представити за допомогою гіперболічних функцій:

(3.17)

Підставляючи це рішення у вираз функції , одержимо бігармонічну функцію у вигляді

Аналогічно можна показати, що функція

також є бігармонічною і може бути застосована для рішення плоскої задачі.

Якщо числу в співвідношенні (г) давати різні значення, то щораз будуть виходити нові функції, що відрізняються значеннями параметра 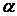й постійних , , , . Тому загальне рішення бігармонічного рівняння (3.11) може бути представлене як сума всіх його можливих часних рішень, тобто у вигляді нескінченного ряду

(3.18)

Постійні , ,…, , визначаються з умов на контурі. Навантаження на контурі повинно бути розкладено в тригонометричний ряд Фур'є по синусах і косинусам.

За допомогою функції напружень (3.18), додаючи якщо буде потреба статечні поліноми, можна одержати рішення для більш широкого кола задач, чим за допомогою тільки статечних поліномів. Серед них можна назвати задачу про згинання балки-стінки, задачу про дію на пластинку навантажень, розподілених уздовж контура за будь-яким законом (у тому числі зосередженої сили).

3. Метод кінцевих різниць (метод сіток). Точне рішення бігармонічного рівняння плоскої задачі в багатьох випадках виявляється дуже складним. Для його спрощення можна застосувати наближений метод кінцевих різниць, що дозволяє замінити диференціальне рівняння системою лінійних алгебраїчних рівнянь.

Установимо залежності між похідними функції в довільній точці і значеннями самої функції в цій і в сусідніх точках. На рис. 3.3 зображена крива і показані п'ять точок, абсциси яких відрізняються на малу величину . По визначенню похідна функції в точці

Рис. 3.3. Крива і п'ять близько розташованих точок

Якщо інтервал між двома точками малий, то похідну в точці приблизно можна представити так:

(д)

Аналогічно можна представити похідну в точці 1:

і в точці :

Другу похідну в точці можна одержати, використовуючи двічі
подання першої похідної:

Зменшивши інтервал у два рази, можна одержати більш точне значення другої похідної в точці :

(e)

Далі обчислюємо третю похідну в точці :

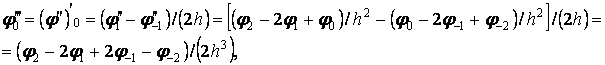
(ж)

а потім і четверту:

(з)

У випадку плоскої задачі функція буде залежати від двох координат 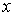і 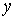, тому з'явиться необхідність виражати через кінцеві різниці частні похідні. Для цього досліджувану плоску область (рис. 3.4) розбивають сіткою на осередки з розмірами й . Для спрощення розрахунків сітку вибирають із квадратними осередками, тобто приймають . Частки похідні функції в точці можуть бути виражені через значення функції в 13 точках, пронумерованих на зазначеному рисунку.

Рис. 3.4. Розбивка досліджуваної плоскої області

Перші й другі похідні в точці по одній з координат легко скласти за аналогією з формулами (д) і (е):

	(и)
	(к)

Другу змішану похідну в точці знайдемо, застосувавши двічі формули (і):

(л)

Четверті частки похідні по одній з координат у точці складемо відповідно до формули (з):

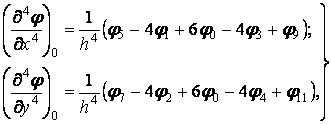
(м)

а змішану похідну знайдемо, застосовуючи двічі формулу (к):

(н)

Зв'язок між функціями в 13 розглянутих точках установимо за допомогою бігармонічного рівняння плоскої задачі (3.11). У точці воно приймає такий вид:

Підставляючи в нього вираз четвертих похідних (м) і (н), одержуємо

(3.19)

Напруги в точці знайдемо за допомогою формул (3.10) без урахування об'ємних сил:

(3.20)

Рівняння виду (3.19) можна скласти для кожного з вузлів усередині контуру; при цьому в частину рівнянь увійдуть і значення функцій для вузлів на контурі і для вузлів; розташованих на відстані одного кроку поза контуром. На рис. 3.4 позаконтурна сітка показана штриховими лініями.

Значення функції на контурі й поза контуром знаходять із граничних умов. Таким чином, невідомих значень функції виявиться стільки, скільки вузлів усередині контуру, але стільки ж можна скласти і рівнянь виду (3.19). Отже, для рішення задачі рівнянь досить.

Для визначення значень функції на контурі і поза ним використовуємо ідеї проф. А. П. Сініцина, що запропонував розглядати значення функції на контурі досліджуваної області як згинальний момент у балці з таким же навантаженням, що й на даному краї області. Дійсно, якщо на верхній грані прямокутної області прикладене навантаження , спрямоване донизу, то для цієї грані можна скласти наступну умову:

(о)

Порівнюючи ії із залежністю між згинальним моментом і інтенсивністю розподіленого навантаження при згинанні балок

заключаємо, що функцію напружень на контурі пластинки можна прийняти за значення згинального моменту в даній точці балки з таким же навантаженням. При цьому балка може мати будь-яке закріплення, тому що його характер впливає тільки на значення постійних, що з'являються після інтегрування співвідношення (о):

(п)

На напруження вид закріплення балки впливу не зробить, оскільки напруження дорівнюють другим похідним функції і постійні , у їх вирази не ввійдуть. На нижній грані пластинки функцію варто брати рівною значенню згинального моменту зі зворотним знаком.

Похідні функції на верхній і нижній гранях , а на бічних — являють собою поперечні сили у відповідних точках балки.

Похідні на верхній і нижній гранях і 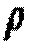на бічні можна знайти з формули

Значення похідних у точках контуру можна використовувати і для визначення значень функції в точках поза контуром.

Так, для точки 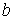(рис. 3.4) відповідно до формули (і) можна скласти наступне співвідношення:

Звідси знаходимо значення функції в точці 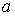, розташованої поза контуром пластинки:

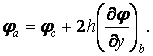
(3.21)

Точно так само для точки 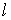, що лежить на бічній грані,

звідки значення функції в точки 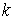, що лежить поза контуром пластинки,

(3.22)

Таким чином, плоска задача зведена до відшукання значень функції у всіх вузлах сітки. Для цього, як відзначалося вище, маємо стільки рівнянь виду (3.19), скільки вузлів усередині пластинки. Значення функції на контурі пластинки знаходимо із граничних умов за допомогою співвідношень (п), а поза контуром — за допомогою співвідношень (3.21) і (3.22). Вирішуючи систему рівнянь виду (3.19), знаходимо значення функції , а за допомогою рівнянь (3.20) визначаємо напруження у всіх вузлах сітки.

Метод кінцевих різниць виявляється особливо ефективним при використанні комп'ютерної техніки. Цей метод вимагає багаторазового циклічного повторення розрахунку по тим самим формулах для кожного інтервалу. Він зводить рішення до виконання найпростіших арифметичних дій.

Система лінійних алгебраїчних рівнянь типу (3.19) добре піддається програмуванню. Зі збільшенням частоти сітки підвищується точність розрахунку.

Застосування методу кінцевих різниць особливо ефективно при розрахунку складних пластинок, коли контур непрямокутний, коли пластинка має отвори і т.д.