 |
|
Прямокутна пластинка. Рішення Нав’є
Рішення основного рівняння згинання (5.15) для прямокутної пластинки в замкнутій формі одержати не вдається. Його доводиться шукати у вигляді нескінченного ряду. Розглянемо шарнірно обперту по контуру прямокутну пластинку (рис. 5.9), що перебуває під дією поперечного навантаження інтенсивністю 
, що змінюється за будь-яким законом. Початок координат розташуємо в куті пластинки. Розмір пластинки в напрямку осі 
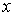дорівнює 
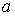, а в напрямку осі 
— 
.
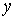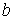Рис. 5.9. Шарнірно обперта пластинка
Рішення рівняння (5.15) будемо шукати у вигляді подвійного тригонометричного ряду по синусах:
, (а)
де 
— постійні числа, коефіцієнти ряду; 
і 
— цілі позитивні числа: 1, 2, 3, …
Ряд (а) можна представити в розгорнутому виді:
Для шарнірно обпертої по контуру пластинки маємо наступні граничні умови:
при 
й 
; (а)
при 
й 
. (б)
Переконаємося, що ряд (а) задовольняє цим умовам. Дійсно, на грані пластинки 
й, отже, прогин 
. На грані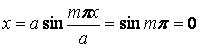 
, а значить, і прогин 
. Точно так само обертаються в нуль прогини на гранях і .
Отже, граничні умови (б) і (в) відносно прогинів виконуються.
Другі похідні функції прогинів
містять синуси тих же аргументів, що і сама функція. Тому похідні звертаються в нуль на всіх гранях пластинки: при 
, 
, 
і 
. Отже, граничні умови (б) і (в) для згинальних моментів також виконуються.
Визначимо коефіцієнти ряду (а). Для цього підрахуємо четверті похідні функції прогинів
і підставимо їх у рівняння (8.15). Після спрощення одержимо
| (г) |
Щоб визначити коефіцієнти ряду, що входить у ліву частину рівняння (г), необхідно і праву частину цього рівняння розкласти в тригонометричний ряд. Представимо навантаження у вигляді подвійного тригонометричного ряду Фур'є по синусах у прямокутній області 
; 
:
| (д) |
Коефіцієнти цього ряду визначаються по формулі, відомої з курсу математичного аналізу:
| (е) |
Підставляючи ряд (д) у рівняння (г), одержуємо
.
Два ряди рівні між собою, якщо рівні їх відповідні члени. Таким чином,
Підставляя сюди замість 
вираз (е), знаходимо коефіцієнти ряда (а) у такій формі:
| (ж) |
Отже, функція (а) є рішенням поставленої задачі, тому що вона задовольняє умовам на контурі пластинки і при виборі коефіцієнтів ряду у формі (ж) задовольняє основному рівнянню згинання пластинки. Подальша конкретизація задачі залежить від виду функції 
.
Розглянемо деякі окремі випадки.
1. Навантаження рівномірно розподілене по всій поверхні пластинки (рис. 5.10). У цьому випадку 
.
Рис. 5.10. Вплив розподіленого навантаження
Тоді, відповідно до формули (ж),
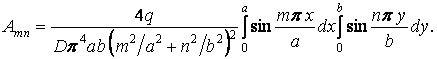
| (з) |
Після інтегрування одержуємо
Підставляючи значення цих коефіцієнтів у ряд (а), знаходимо вираз функції прогинів:
| (5.20) |
Максимальний прогин, що виникає в центрі пластинки (при 
й 
), становить
Підставляючи сюди значення циліндричної жорсткості (5.7) і виносячи за дужки 
, одержуємо
Для практичного використання одержуваних результатів формують таблиці. У цих цілях останню формулу зручно представити в такому вигляді: 
де коефіцієнт
залежить тільки від відношення сторін пластинки 
. Ряд, що входить сюди швидко сходиться. Так, зберігаючи перші чотири члени ряду й приймаючи 
, для квадратної пластинки 
знаходимо
що відповідає точному значенню, що приводиться в довідковій літературі.
Підставляючи функцію прогинів (5.20) у формули (5.8), одержимо згинальні моменти:
Максимальні згинальні моменти виникають у центрі пластинки (при 
й 
):
Для складання таблиць їх представляють у вигляді
де коефіцієнти 
і 
є функціями відношення сторін пластинки . Ряди в цих функціях сходяться повільніше, ніж у функції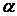 
. Так, якщо підрахувати коефіцієнт для квадратної пластинки, зберігаючи перші чотири члени ряду, одержимо
у той час як точне значення, що приводиться в таблицях, 
. Отже, при збереженні чотирьох членів ряду значення коефіцієнта відрізняється від точного його значення на 2,1 %.
Значення поперечних сил знайдемо, підставивши функцію прогинів (5.20) у формули (5.9):
Максимальні значення поперечні сили одержують посередині сторін контуру пластинки. Так, 
виникає в точках з координатами 
й 
, a 
— у точках з координатами 
й 
:
Для табулювання ці функції представляють у такому вигляді:
де коефіцієнти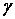 
і 
є функціями відношення сторін пластинки 
. Ряди в цих функціях сходяться ще повільніше, ніж у функціях ,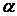 
, і . Так, зберігаючи, як і в попередніх випадках, те ж число членів ряду, для квадратної пластинки одержуємо
що відрізняється від точного значення, рівного 0,338, на 16,3%.
2. Сила P зосереджена в точці K з координатами 
й 
(рис. 5.11).
Рис. 5.11. Вплив зосередженої сили
Представимо цю силу у вигляді навантаження, розподіленого на нескінченно малій площі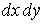 
навколо точки K:
При обчисленні подвійного інтеграла у формулі (ж) варто врахувати, що він звертається в нуль у всіх точках, крім K, де він дорівнює
Підставляючи це значення в зазначену формулу, одержуємо вираз коефіцієнтів ряду (а):
а підставляючи цей вираз в ряд (а), знаходимо функцію прогинів пластинки:
| (5.21) |
Отриманий ряд сходиться повільніше, ніж ряд (5.20).
Знаючи функцію прогинів, звичайним шляхом можна знайти згинальні моменти, поперечні сили й крутні моменти. Ряди, що входять у них, сходяться ще гірше, тому викладена методика може бути рекомендована тільки для знаходження прогинів. Для обчислення ж згинальних моментів, а тим більше, поперечних сил, вона нераціональна.