 |
|
Найпростіші осесиметричні задачі вигину круглої пластинки
Задача про вигин круглої пластинки буде осесиметричною, якщо навантаження на пластинку, а також умови закріплення її країв не залежать від полярного кута 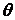 . У цьому випадку прогини пластинки також не залежать від полярного кута
. У цьому випадку прогини пластинки також не залежать від полярного кута 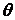 , а є функцією лише координати r, тобто
, а є функцією лише координати r, тобто 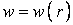 . Тоді рівняння (5.22) значно спрощується:
. Тоді рівняння (5.22) значно спрощується:

| (5.27) |
Формули згинальних моментів (5.23) приймають вигляд
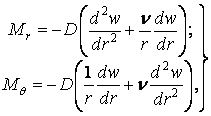
| (5.28) |
а крутний момент (5.24) звертається в нуль.
Спрощуються й вирази поперечних сил (5.25)

| (5.29) |
а наведені поперечні сили на контурі (5.26) становлять
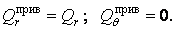
Рівняння (5.27) можна вирішити в загальному виді. Як відомо, загальний розв’язок неоднорідного диференціального рівняння складається із суми загального розв’язку відповідного однорідного рівняння 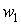 і якого-небудь частинного розв’язку неоднорідного рівняння
і якого-небудь частинного розв’язку неоднорідного рівняння  , тобто
, тобто
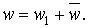
| (а) |
Загальний розв’язок однорідного рівняння
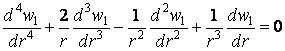
записується так:
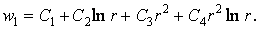
Щоб одержати частинний розв’язок 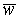 , рівняння (5.27) можна скласти у вигляді
, рівняння (5.27) можна скласти у вигляді

Переконатися в правильності цього рівняння можна, виконавши диференціювання в його лівій частині. Диференціюючи функцію, що розташовується в круглій дужці, знаходимо

або

Диференціюючи функцію, що розташовується в прямих дужках, одержимо

або

Нарешті, диференціюючи функцію, що розташовується у фігурних дужках, знаходимо

або

що збігається з рівнянням (5.27).
Інтегруючи це рівняння послідовно чотири рази, знайдемо загальний вигляд частинного розв’язку:

| (б) |
Нехай навантаження рівномірно розподілене по всій поверхні пластинки, тобто  . У цьому випадку вираз (б) легко інтегрується й приводить до наступного результату:
. У цьому випадку вираз (б) легко інтегрується й приводить до наступного результату:

Отже, загальний розв’язок неоднорідного диференціального рівняння (5.27) при рівномірно розподіленому навантаженні такий:
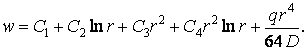
| (5.30) |
Розглянемо деякі приклади розрахунку пластинок, що перебувають під дією рівномірно розподіленого навантаження.
1. Суцільна шарнірно обперта по контурі пластинка (рис. 5.16).
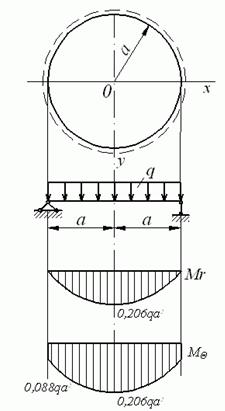
Рис. 5.16. Шарнірно обперта по контурі пластинка
Для визначення постійні інтегрування маємо наступні граничні умови. У центрі пластинки (при 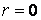 ) прогин повинен мати кінцеве значення. Тому що
) прогин повинен мати кінцеве значення. Тому що  , то в розв’язку (5.30) варто відкинути члени, що містять множник
, то в розв’язку (5.30) варто відкинути члени, що містять множник 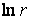 , тобто прийняти
, тобто прийняти

Тоді
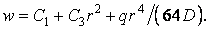
| (в) |
Дві умови маємо на контурі пластинки, де повинні звертатися в нуль прогин 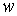 і радіальний згинальний момент
і радіальний згинальний момент  . Таким чином, при
. Таким чином, при 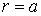
 і і 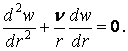
| (г) |
Підставляючи в умови (г) функцію прогинів (в), одержуємо:
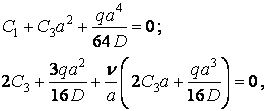
звідки
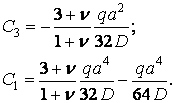
Підставляючи знайдені постійні в розв’язок (в), одержуємо функцію прогинів для розглянутої пластинки:
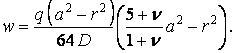
| (5.31) |
Максимальний прогин виникає в центрі пластинки (при 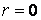 ):
):
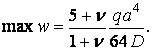
| (д) |
Підставляючи функцію прогинів (5.31) у формули (5.28), знаходимо згинальні моменти в пластинці:

| (5.32) |
Максимальні згинальні моменти також виникають у центрі пластинки:
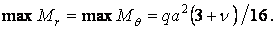
Згинальні моменти в точках контуру (при 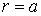 ):
):

Епюри згинальних моментів для пластинки, виготовленої з матеріалу з коефіцієнтом Пуассона  , показані на рис. 5.16.
, показані на рис. 5.16.
2. Суцільна затиснена по контурі пластинка (рис. 5.17).
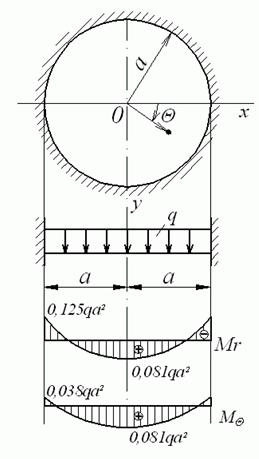
Рис.5.17. Затиснена по контурі пластинка
Для визначення сталих  і
і 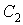 маємо наступні граничні умови: на зовнішньому контурі пластинки повинні біти відсутніми прогини й повороти перерізів, тобто
маємо наступні граничні умови: на зовнішньому контурі пластинки повинні біти відсутніми прогини й повороти перерізів, тобто
при 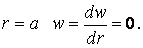
Підставляючи в ці умови функцію прогинів (в), одержуємо:
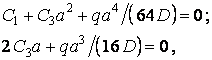
звідки
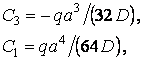
і рівняння серединної поверхні (в) приймає вигляд
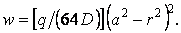
| (5.33) |
Максимальний прогин у центрі пластинки (при 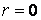 )
)

З порівняння цього результату з формулою (д) випливає, що максимальний прогин затисненої по контурі пластинки в чотири рази менший максимального прогину шарнірно обпертої пластинки.
Підставляючи функцію прогинів (5.33) у формули (5.28), знаходимо згинальні моменти:
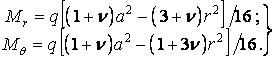
| (5.34) |
Згинальні моменти в центрі пластинки:

на контурі:
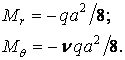
Епюри згинальних моментів для пластинки, виготовленої з матеріалу з коефіцієнтом Пуассона  , показані на рис. 5.17. Максимальний за абсолютним значенням згинальний момент виникає в точках контуру на площадках, перпендикулярних радіусу. Він на 40% менший максимального згинального моменту в шарнірно обпертій пластинці.
, показані на рис. 5.17. Максимальний за абсолютним значенням згинальний момент виникає в точках контуру на площадках, перпендикулярних радіусу. Він на 40% менший максимального згинального моменту в шарнірно обпертій пластинці.
3. Кільцева пластинка із затисненим зовнішнім краєм (рис. 5.18).
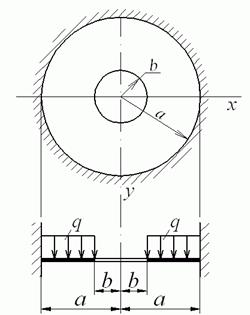
Рис. 5.18. Кільцева пластинка із затисненим зовнішнім краєм
Для визначення постійних інтегрування, що входять у розв’язок (5.30), маємо наступні граничні умови: на зовнішньому, затисненому краї (при 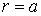 )
)

на внутрішньому, вільному краї (при 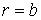 )
)

і 
Підставляючи в ці умови функцію прогинів, (5.30), одержимо систему рівнянь:

Розв’язавши цю систему, знаходимо
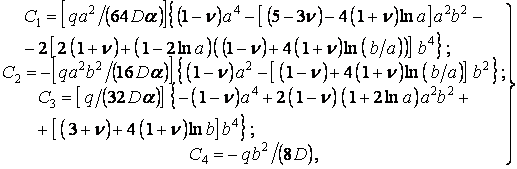
| (е) |
де
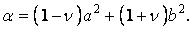
Якщо ввести позначення

то рівняння серединної поверхні пластинки (5.30) після підстановки в нього сталих (е) прийме наступний вигляд:

| (5.35) |
Подальший хід розрахунку, тобто визначення зусиль і напруг не представляє складнощів і проводиться аналогічно попереднім прикладам.