Главная | Обратная связь

Поняття про розрахунок гнучких пластинок

Тонкі пластинки, що мають прогини більші чверті своєї товщини, називаються гнучкими. Для них гіпотеза про недеформованість серединної площини виявляється несправедливою, тому що в ній виявляються деформації розтягання, стиску й зрушення. Крім того, зусилля серединної площини гнучкої пластинки залежать від її прогинів.

При більших прогинах точки серединної площини одержують переміщення й уздовж осей x і y (рис. 5.19).

Рис. 5.19. Переміщення в гнучкій пластинці

Тоді формули (5.4) приймають вигляд

Точно так само у формулах (5.5) з'являються деформації точок серединної площини , і :

Ці формули ускладнюються ще й тим, що деформації точок серединної площини залежать від прогинів нелінійно:

(5.36)

тому що в цьому випадку квадрати похідних і 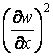мають той же порядок малості, що й похідні й .

Напруги в гнучкій пластинці приводяться не тільки до згинаючих і крутних моментів і поперечних сил (5.8), (5.9), (5.10), але й до нормальним і зрушуючих сил у серединній площині (рис. 5.20):

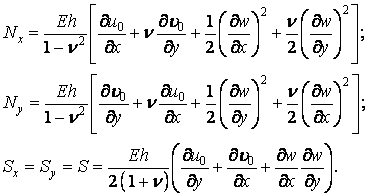
Рис. 5.20. Нормальні й зрушуючі сили

Записані формули містять невідомі складових переміщень точок серединної площини й . Крім цих переміщень, одержуємо рівняння нерозривності деформацій, що зв'язує зусилля в серединній площині пластинки:

(а)

Складемо рівняння рівноваги нескінченно малого елемента серединної площини гнучкої пластинки, що перебуває як під дією поперечних сил, так і під дією сил у її серединній площині (рис. 5.20). Проекція сил на вісь x дає

звідки після спрощення й розподілу на знаходимо

(б)

Аналогічно з рівняння проекцій на вісь y одержуємо

(в)

При проектуванні сил на вісь z гнучку пластинку варто розглядати в деформованому стані. На рис. 5.21 показаний переріз площиною, паралельною 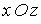, нескінченно малого елемента серединної площини пластинки після скривлення. У цій площині видно сили

і

кути нахилу яких щодо осі відповідно рівні

і

При проектуванні врахуємо, що косинус малого кута дорівнює одиниці, а синус - самому куту, тобто в даній площині

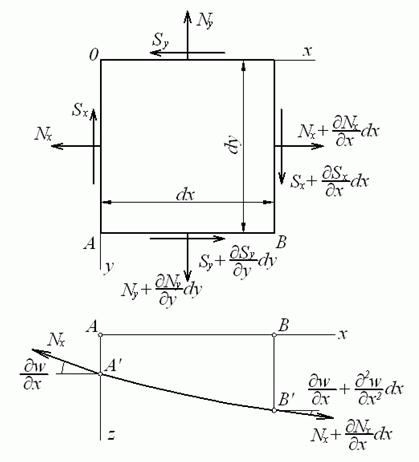
Рис. 5.21. Перетин елемента площиною

Спроектуємо нормальні сили в розглянутій площині на вісь z:

Після спрощення й відкидання величин третього порядку малості одержимо

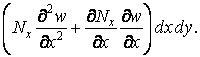
(г)

Аналогічно можна одержати проекцію на вісь z нормальних сил у площині :

(д)

Розташування дотичних сил після деформації гнучкої пластинки показане на рис. 5.22.

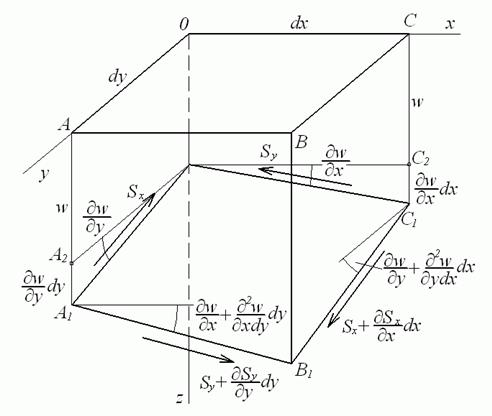
Рис. 5.22. Розташування дотичних сил після деформації

На тому же рисунку показані кути, що формуються цими силами з координатною площиною . Спроектуємо ці сили на вісь z:

Після спрощення й відкидання величин третього порядку малості з урахуванням закону парності дотичних зусиль одержимо

(е)

На проекцію поперечних зусиль скривлення пластинки не впливає, тому беремо її у формі (5.12). Додаючи до цієї залежності проекції (г)—(е), розділені на , після відповідного згрупування одержуємо

Вирази, що знаходяться в дужках, відповідно до співвідношень (б) рівні (в) нулю. Підставляючи потім з (5.9) вирази поперечних сил, знаходимо

(ж)

Якщо ввести функцію Ері у формі

(5.37)

то рівняння (ж) і (а) приймуть вигляд

(5.38)

Тут введений оператор

(5.39)

При цьому оператор виходить із оператора (5.39) заміною функції на функцію .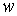

Система нелінійних рівнянь (5.38), що зв'язує функцію напруг у серединній площині пластинки й функцію прогинів, введена німецьким ученим Т. Карманом. Разом із граничними умовами вона представляє основну систему нелінійних диференціальних рівнянь теорії гнучких пластинок. Розв’язок цієї системи в загальному вигляді не отримано. У цей час за допомогою теорії пластинок отриманий ряд частинних розв’язків для рівномірно розподіленого поперечного навантаження, а також для пластинок, що втрачають стійкість при стиску й зрушенні в їхній серединній площині.

У випадку жорсткої пластинки, коли прогини малі в порівнянні з її товщиною, необхідно прийняти функцію . Тоді рівняння (5.38) зводиться до рівняння (5.16).