Главная | Обратная связь

Метод Рітца-Тимошенко

Метод Рітца-Тимошенко заснований на використанні відомого з курсу теоретичної механіки принципу можливих переміщень: для рівноваги системи, підлеглої ідеальним утримуючим зв'язкам, необхідно й досить, щоб сума елементарних робіт всіх прикладених до неї сил на всякому можливому переміщенні рівнялася нулю.

Розглядаючи окремо дію зовнішніх і внутрішніх сил, принцип можливих переміщень можна представити в такий спосіб:

(а)

де — робота зовнішніх сил (об'ємних і поверхневих) на якому-небудь можливому переміщенні; — робота внутрішніх сил, що представляє собою збільшення потенційної енергії на тому ж можливому переміщенні зі зворотним знаком.

Нехай тіло перебуває в рівновазі під дією об'ємних сил, складові яких X, Y, Z, і поверхневих сил, складові яких , , . Позначимо складові можливих переміщень , , і підрахуємо роботу зовнішніх сил на цих переміщеннях. Елементарна робота складової об'ємних сил X, що доводиться на одиниці об'єму, дорівнює добутку цієї сили на об’єм нескінченно малого елемента й на можливе переміщення по її напрямку: .

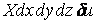Точно так само елементарні роботи складових об'ємних сил Y і Z рівні відповідно , .

Робота, виконувана об'ємними силами в повному об’ємі тіла V дорівнює інтегралу по цьому об’єму від суми елементарних робіт, виконуваних кожною зі складових:

(б)

Елементарна робота складової поверхневих сил , що діє на нескінченно малий елемент поверхні , дорівнює добутку цієї складової на площу й на можливе переміщення в напрямку складової: .

Аналогічно визначаються й елементарні роботи двох інших складових поверхневих сил: , .

Робота, виконувана поверхневими силами, що діють по всій поверхні тіла s, дорівнює інтегралу по цій поверхні від суми елементарних робіт, чинених кожною зі складових поверхневих сил:

(в)

Таким чином, робота всіх зовнішніх сил на можливих переміщеннях дорівнює сумі робіт об'ємних (б) і поверхневих (в) сил:

(г)

При обчисленні можливої роботи зовнішніх сил варіювалися тільки переміщення , і 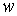, а об'ємні й поверхневі сили залишалися постійними, тому оператор у формулі (г) можна винести за знаки інтегралів і за дужки:

(д)

Збільшення потенційної енергії підраховується відповідно до інтеграла (3.20):

(е)

де W — питома потенційна енергія.

Приймаючи в формулі (а) оператор загальним для обох доданків, одержуємо

(ж)

Вираз, що стоїть в дужках, являє собою роботу всіх зовнішніх і внутрішніх сил, прикладених до тіла. Ця різниця із протилежним знаком є потенційною енергією системи зовнішніх і внутрішніх сил, що діють на пружне тіло:

(6.2)

Вводячи це позначення в умову (ж), одержуємо

(з)

Збільшення функції з точністю до нескінченно малих величин вищого порядку дорівнює її першому диференціалу, тому замість умови (з) можна написати

а це означає, що потенційна енергія системи має екстремальне значення.

У курсі теоретичної механіки доводиться теорема Лагранжа-Діріхле, на підставі якої можна сформулювати наступний принцип мінімуму потенційної енергії: із всіх мислимих переміщень пружного тіла переміщення, що задовольняють умовам стійкої рівноваги, повідомляють потенційної енергії системи мінімальне значення.

Таким чином, потенційна енергія системи (6.2)

(6.3)

де потенційна енергія, що накопичується в пружному тілі, визначається по формулі (1.21), а робота об'ємних і поверхневих сил відповідно до формули (д) становить

(и)

При вигині пластинки об'ємними силами зневажають, а зі складових поверхневих сил відмінна від нуля тільки одна: . Підставляючи це значення у формулу (і) і приймаючи елемент поверхні у вигляді прямокутника зі сторонами й , одержуємо вираз роботи зовнішніх сил при вигині пластинки:

(6.4)

Якщо наближене значення функції прогинів вибирати у вигляді ряду (6.1), то після підстановки цього значення у формулу (6.3) потенційна енергія системи виявиться функцією параметрів :

Визначимо вид цієї функції. Підставивши функцію прогинів (6.1) у формули (2.5) і (2.6), можна переконатися, що складові деформації й напруг є лінійними функціями параметрів . Підставляючи складової деформації й напруг у формулу (1.21), переконуємося, що потенційна енергія є квадратичною функцією цих параметрів. Підставляючи функцію прогинів (6.1) у формулу (6.4), можна переконатися, що робота зовнішніх сил у пластинці є лінійною функцією параметрів . Після підстановки виразів і у формулу (6.3) переконуємося, потенційна енергія системи є квадратичною функцією цих параметрів.

Щоб знайти значення параметрів , що відповідають мінімуму потенційної енергії системи, потрібно прирівняти нулю частини похідні:

(6.5)

Похідна квадратичної функції параметрів виявляється лінійною функцією цих параметрів, тому умова (6.5) являє собою систему лінійних рівнянь щодо параметрів .

Таким чином, метод Рітца-Тимошенко дозволяє замінити задачу про знаходження розв’язку диференціального рівняння вигину пластинки (3.16) задачею про знаходження мінімуму потенційної енергії. Така заміна можлива у зв'язку з тим, що й зазначене диференціальне рівняння й варіаційне рівняння (з) є рівняннями рівноваги пружного тіла. Покажемо, що останнє містить у собі диференціальні рівняння рівноваги й умови на поверхні. Розглядаючи рівняння (з) у формі

(к)

внесемо в нього вирази потенційної енергії (1.20) і (1.16), можливу роботу всіх зовнішніх сил (г) і врахуємо, що

В результаті одержимо

Звернемося в рівнянні (л) до першого з потрійних інтегралів і зробимо інтегрування по змінній x. Інтегруючи вроздріб, знаходимо

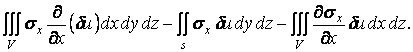
(м)

Перший інтеграл у правій частині рівності (м) є поверхневим інтегралом другого типу. Його можна перетворити в поверхневий інтеграл першого типу по відомій з курсу математичного аналізу формулі

(н)

Тут функції повинні бути безперервними разом з першими частинними похідними усередині об’єму обмеженого поверхнею s; l, m, n — напрямні косинуси нормалі до цієї поверхні.

Використовуючи перетворення (н), замість формули (м) одержуємо

Аналогічно перетворяться й інші вісім перших потрійних інтегралів у рівнянні (л). Після перетворення й групування по складових можливих переміщень замість рівняння (л) одержуємо

У записаному рівнянні можливі переміщення , , між собою не зв'язані, тому, щоб воно зверталося в тотожність при будь-яких значеннях можливих переміщень, повинні звертатися в нуль коефіцієнти при можливих переміщеннях, що стоять у дужках. Отже, одержуємо шість рівнянь: три перших рівняння являють собою умови на поверхні (2.2), а три інших - диференціальні рівняння рівноваги (2.1). Таким чином, варіаційне рівняння (к) містить у собі диференціальні рівняння рівноваги й статичні граничні умови. Звідси треба, що при використанні цього рівняння для наближеного розв’язку задачі обрана функція обов'язково повинна задовольняти тільки геометричним граничним умовам. Статичні граничні умови й основне диференціальне рівняння задачі задовольняються автоматично.

Отже, розв’язок задачі про вигин пластинки методом Рітца-Тимошенко полягає в наступному. Приймаємо наближене значення функції прогинів у формі подвійного ряду

(о)

причому функції повинні задовольняти геометричним граничним умовам. Обчислюємо наближене значення потенційної енергії в пластинці , для чого нижче отримана формула (6.11). По формулі (6.4) обчислюємо роботу зовнішніх сил , а по формулі (6.3) — потенційну енергію системи . Для визначення параметрів використовуємо систему рівнянь (6.5). Знайдені параметри підставляємо у функцію прогинів (о) і одержуємо шуканий наближений розв’язок.

Варто помітити, що, хоча задоволення статичних граничних умов у методі Рітца-Тимошенко не обов'язкове, функції краще по можливості вибирати так, щоб вони задовольняли всім граничним умовам — геометричним і статичним. У цьому випадку ряд швидше сходиться до точного розв’язку й при обчисленнях буває досить обмежитися одним-двома членами ряду.