 |
|
Приклад розв’язання задачі методом Рітца-Тимошенко
Для ілюстрації методу Рітца-Тимошенко розглянемо вигин прямокутної пластинки, шарнірно обпертої по контурі й навантажену рівномірно розподіленим навантаженням (рис. 6.2).
Рис. 6.2. Розв’язання методом Рітца-Тимошенко
Наближений вираз функції прогинів приймаємо у вигляді ряду
| (а) |
де функції
задовольняють всім граничним умовам шарнірного обпирання - і геометричним, і статичним.
Для обчислення коефіцієнтів ряду 
визначимо потенційну енергію системи зовнішніх і внутрішніх сил (6.2). Попередньо підрахуємо оператор Лапласа над функцією 
:
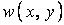і підставимо цей вираз у формулу (6.11):
| (б) |
Зведення у квадрат подвійного ряду рівносильне перемножуванню двох багаточленів, де кожний член першого ряду множиться на кожний член другого ряду. Щоб відрізнити члени одного ряду від членів іншого, в одному з них індекси k і l замінимо відповідно на c і d. Тоді вираз, що стоїть у квадратних дужках під інтегралом у формулі (б), перетвориться в такий спосіб:
Підставимо цей ряд у формулу (б). Міняючи порядок інтегрування, і підсумовування, а також виносячи постійні величини за знак інтеграла, одержуємо
| (в) |
Досліджуємо вхідні сюди інтеграли. Перший з них
тобто цей інтеграл відмінний від нуля тільки при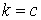 
. У цьому випадку він дорівнює
Аналогічно, другий інтеграл
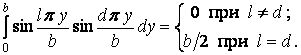
Підставляючи ненульові значення інтегралів у формулу (в) і з огляду на те, що вони відмінні від нуля тільки при значеннях індексів підсумовування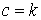 
й 
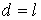, знаходимо
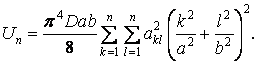
| (г) |
Роботу зовнішніх сил при вигині пластинки під дією поперечного навантаження можна підрахувати по формулі (6.4). Підставимо в цю формулу функцію прогинів 
і врахуємо, що 
:
Інтегруючи, одержуємо
| (д) |
Підставимо співвідношення (г) і (д) у формулу (6.2), зберігаючи в обох рядах тільки члени, що містять непарні індекси k і l (при парних індексах коефіцієнти 
):
Коефіцієнти 
потрібно вибирати так, щоб потенційна енергія системи мала мінімум, тобто повинні виконуватися умови (6.5):
Звідси знаходимо значення постійних коефіцієнтів:
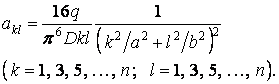
Підставимо ці коефіцієнти в рівняння прогинів (а) і винесемо за знак суми постійний множник 
:
| (е) |
Якщо у формулі (е) взяти нескінченно велику кількість членів, тобто прийняти 
, то одержимо розв’язок задачі, що збігається з точним (8.20).
Розглянемо наближений розв’язок, обмежуючись одним членом ряду. Тоді з формули (е) маємо
| (ж) |
Максимальний прогин виникає в центрі пластинки (при 
й 
):
У квадратній пластинці, коли 
, максимальний прогин
Підставляючи в цю формулу вираз циліндричної жорсткості (8.7) і приймаючи коефіцієнт Пуассона 
, знаходимо
Це наближене значення відрізняється від точного, рівного 
, усього на 2,7%.
Згинальні моменти знайдемо по формулах (8.8), підставляючи функцію прогинів у першому наближенні (ж):
Максимальні згинальні моменти також виникають у центрі пластинки:
У квадратній пластинці
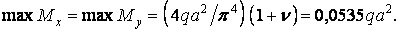
Точне значення, що приводиться в довідниках, становить 
. Отже, максимальний згинальний момент для квадратної пластинки, підрахований у першому наближенні, відрізняється, від точного значення на 11,7%. Тому при обчисленні згинальних моментів у розглянутій пластинці варто брати кілька членів ряду (е). Ще менш точний результат виходить при обчисленні в першому наближенні поперечних сил.