 |
|
Задача теплопроводности в тонком стержне. Метод Фурье – разделения переменных
Рассмотрим тонкий изолированный (покрытый тепловой изоляцией) стержень, лежащий на отрезке 
оси 
(рис. 124). Предполагается, что его физические свойства в точках любого его сечения одинаковы. Температура стержня есть функция
от абсциссы сечения и времени 
.
На основании сказанного в § 5.1 функция 
удовлетворяет дифференциальному уравнению в частных производных
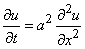, (1)
где 
- константа, если предположить, что теплоемкость и теплопроводность стержня не зависят от .
Рис. 124
Поставим задачу: найти функцию 
, непрерывную для 
, имеющую непрерывные частные производные 
и 
для 
, удовлетворяющую дифференциальному уравнению (1) для , и следующим условиям:
1) начальному условию
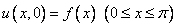, (2)
где 
- заданная на отрезке непрерывная функция;
2) граничным условиям
. (3)
Таким образом, предполагается, что в начальный момент времени 
температура в стержне выражается функцией (см. (2)), а на протяжении всего времени опыта на концах стержня искусственно поддерживается температура нуль (см. (3)).
Уравнение (1) будем решать методом Фурье разделения переменных. Суть его заключается в том, что мы отыскиваем частные решения уравнения (1), удовлетворяющие пока только краевым условиям (3), в виде произведения двух функций, каждая из которых зависит только от одного переменного:
. (4)
При этом мы ищем нетривиальные решения, т. е. тождественно не равные нулю. Из (4) имеем
.
Подставляя эти выражения в (1), получаем
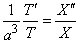. (5)
В (5) левая часть не зависит от , а правая – от , поэтому
, (6)
где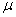 
- некоторая постоянная.
Таким образом, функция 
и 
удовлетворяют обыкновенным дифференциальным уравнениям
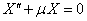, (7)
, (8)
где 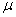- некоторая постоянная.
Так как мы ищем решения, удовлетворяющие условиям (3), то при всех должны выполняться равенства
.
Если предположить, что 
, то 
для всех и . Поэтому имеется хотя бы одно , для которого 
. Но тогда
. (9)
Метод Фурье – разделения переменных
Классический метод решения дифференциального уравнения теплопроводности состоит в том, что находится совокупность частных решений 
, удовлетворяющих уравнению и граничному условию, а затем по принципу наложения составляется ряд этих решений:
. (2.1)
Коэффициенты 
находятся из начального условия.
Строго говоря, это свойство наложения для бесконечного ряда нуждается в специальном обосновании, так как оно безоговорочно справедливо только для конечной суммы. Такое обоснование состоит в том, что необходимо доказать равномерную сходимость ряда, полученного после дифференцирования ряда (2.1), а также законность почленного интегрирования ряда при определении коэффициентов . Это обоснование можно найти в монографиях по математической физике.
Частное решение Т ищется в виде произведения двух функций, одна из которых 
зависит только от времени 
, а другая 
зависит только от координат, т. е. [1]
, (2.2)
где С – произвольная постоянная.
Если подставим решение (2.2) в уравнение (2.1), то получим
;
это равенство можно написать еще так:
. (2.3)
Левая часть равенства может зависеть только от или быть постоянным числом, но она не зависит от координат. Правая часть может зависеть только от координат или быть постоянным числом, но она не зависит от времени. Равенство должно иметь место при любых значениях времени и координат. Это возможно только в том случае, если правая и левая части равенства равны некоторой постоянной величине D, т. е.
; (2.4)
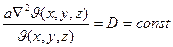. (2.5)
Уравнение (2.4) можно проинтегрировать, и тогда получим
. (2.6)
Постоянную интегрирования не пишем, поскольку ее можно отнести к постоянной C.
Постоянная величина D выбирается из физических соображений. Для тепловых процессов, стремящихся к температурному равновесию, когда по истечению длительного промежутка времени 
должно установиться определенное распределение температуры, величина D не может быть положительной величиной, она будет только отрицательной. Если D есть величина положительная, то при длительном промежутке времени температура будет больше наперед заданной величины, т. е. стремится к бесконечности, что противоречит сущности процесса.
Если температура тела есть периодическая функция времени, например в случае распространения тепловых волн в теле, то величина D должна быть мнимой величиной, чтобы простой экспоненты (2.6) получить периодическую функцию времени.
Рассмотрим первый случай, когда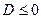 
. Так как величина D пока произвольная постоянная по числовому значению, то можно положить
, (2.7)
где а – коэффициент температуропроводности (величина положительная), k – некоторая постоянная, которая определяется из граничных условий. Подставляя эти значения для D, получим:
, (2.8)
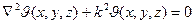. (2.9)
Дифференциальное уравнение (2.9) часто называют уравнением Покеля; оно хорошо изучено в математической физике.
Таким образом, применяя метод Фурье, уравнение теплопроводности сводим к уравнению типа Покеля, решение которого определяется геометрической формой тела, начальным распределением температуры, а также условиями теплообмена тела с окружающей средой или окружающими телами.