Главная | Обратная связь

Термодинамический потенциал Гиббса.

Так называется функция состояния, определяемая следующим образом:

. (2.13)

Её полный дифференциал равен

.

Следовательно, естественными переменными для функции являются и . Частные производные этой функции равны

.

Метод термодинамических потенциалов будет продемонстрирован в дальнейшем при изложении теории эффекта Джоуля-Томсона, а также метода адиабатического расширения реального газа.

 

Контрольные вопросы:

1. Дайте определение обратимого и необратимого процесса.

2. Что представляет собой тепловая машина? Чему равен КПД тепловой машины?

3. Из каких изопроцессов состоит цикл Карно? Начертите график цикла Карно в координатах P и V.

4. Получите формулу для КПД цикла Карно.

5. Дайте определение энтропии. Получите формулы для подсчета изменения энтропии идеального газа для изопроцессов.

6. Начертить графики изопроцессов в координатах Т и S. Какой физический смысл имеет площадь под графиком газового процесса в координатах Т и S?

7. Начертить цикл Карно в координатах Т и S. Приведите теорему Карно для обратимого и необратимого цикла Карно.

8. Сформулируйте второе начало термодинамики. Чему равно изменение энтропии для обратимых и необратимых процессов?

9. Получите основное термодинамическое неравенство Клаузиуса.

10. Объясните, в чем заключается статистический смысл второго начала термодинамики.

11. Перечислите термодинамические потенциалы и дайте определение каждого из них. Чему равен полный дифференциал данных термодинамических потенциалов?

 

Реальные газы

Поведение газов хорошо описывается уравнением Менделеева-Клайперона

(3.1)

только при малых плотностях, т.е. при не слишком больших давлениях и достаточно высоких температурах. С повышением давления и уменьшением температуры наблюдается значительные отступления от этого уравнения. Во втором столбце таблицы 3.1 приведены значения произведений PV, для массы азота, занимающей при нормальных условиях объем, равный одному литру. Указанные значения даны для различных давлений и одной и той же температуры 0°С.

Таблица 3.1

P, атм	PV, а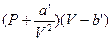тм×л	, атм×л
	1.000 0.994 1.048 1.390 2.069	1.000 1.000 1.009 1.014 0.893

В соответствии с уравнением (3.1) произведение PV при неизменной температуре должно оставаться постоянным. В действительности, как видно из таблицы 3.1, при давлениях порядка 200 атм. наблюдаются заметные отклонения, которые непрерывно возрастая с увеличением давления, достигают при 1000 атм. более 100%. Эти отклонения не представляются удивительными, поскольку при увеличении плотности начинают играть все большую роль объем молекул и взаимодействие между ними.

Уравнение состояния реального газа

Для описания поведения газов в широком интервале плотностей было предложено много различных уравнений. Самым простым из них и вместе с тем дающим достаточно хорошие результаты оказалось уравнение Ван-дер-Ваальса. Это уравнение получено путем внесения поправок в уравнение (3.1):

. (3.2)

1) Во-первых, из-за взаимного притяжения между молекулами газ как бы сжимается большим давлением, чем давление Р, оказываемое на газ стенками сосуда, в котором он заключен. Поправка Р_i характеризует ту добавку к внешнему давлению, которая обусловлена взаимным притяжением молекул друг к другу. Заметное воздействие молекул друг на друга осуществляется в пределах небольших расстояний, называемых радиусом молекулярного действия. Сила взаимного притяжения двух элементарных объемов, имеющих радиусы порядка этого радиуса, пропорциональна как числу молекул, заключенных в одном из объемов, так и числу молекул, заключенных в другом объеме. Каждое из этих чисел в свою очередь пропорционально числу молекул в единице объема, т.е. обратно пропорционально объему газа. Этими соображениями можно пояснить то обстоятельство, что поправка к давлению имеет вид:

,

где а – постоянная.

2) Во-вторых, вследствие того, что молекулы обладают конечным объемом, пространство, доступное для движения молекул, оказывается меньшим, чем объем сосуда V. Поправка к объему V_i характеризует ту часть объема, которая недоступна для движения молекул. Она равна по порядку величины нескольким суммарным объемам молекул, и пропорциональна количества вещества n:

,

где b – еще одна постоянная.

Тогда уравнение Ван-дер-Ваальса для данной массы газа примет вид:

, (3.3)

где a и b – константы Ван-дер-Ваальса, имеющие для разных газов различные значения, определяемые опытным путем (см. табличные значения). Если давление выражено в паскалях, а объем в м³, то константа a измеряется в Па×м⁶/моль², а константа b – в м³/моль. Можно ввести константы Ван-дер-Ваальса для данной массы газа:

.

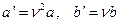Насколько уравнение Ван-дер-Ваальса лучше передает поведение газов, чем уравнение (3.1) можно судить по данным, приведенным в таблице 3.1. В третьем столбце таблицы даны значения величины 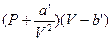для той же массы азота, для которой даны во втором столбце значения PV. Как видно из таблицы 3.1, уравнение Ван-дер-Ваальса (3.3) гораздо лучше согласуется с экспериментом, чем уравнение (3.1).

В соответствии с тем фактом, что все реальные газы с уменьшением плотности приближаются по своим свойствам к идеальному газу, уравнение Ван-дер-Ваальса в пределе, при стремление объема к бесконечности, переходит в уравнение (3.1). В этом можно убедиться, вынося в уравнение Ван-дер-Ваальса P и V за скобки:

,

и приняв во внимание, что произведение PV остается примерно постоянным.

Изотермы Ван-дер-Ваальса. Параметры критического состояния вещества

Наиболее содержательные результаты получаются из уравнения Ван-дер-Ваальса путем анализа его изотерм. Для одного моля газа (n = 1) уравнение изотермы можно представить в виде

, (3.4)

если считать температуру Т постоянной. Перепишем уравнение (3.4) в виде:

. (3.5)

При высоких температурах последний член в (3.5) можно опустить, и тогда изотерма будет гиперболой, асимптотами которой являются изобара (Р = 0) и изохора (V = b) .

Для исследования изотерм при любых значениях Т умножим уравнение (3.4) на V². После раскрытия скобок уравнение изотермы примет вид

. (3.6)

Это уравнение третьей степени по V , в которое давление Р входит в качестве параметра. Поскольку его коэффициенты вещественны, уравнение имеет либо один вещественный корень, либо три корня. Каждому корню на плоскости (V,P) соответствует точка, в которой изобара Р = const пересекает изотерму. В первом случае, когда корень один, точка пересечения будет одна. Так будет, как мы видели, при любых давлениях, если температура достаточно высокая. Изотерма имеет вид монотонно опускающейся кривой MN (рис. 3.1).

При более низких температурах и надлежащих значениях давления Р уравнение (3.6) имеет три корня V₁, V₂, V₃ . В таких случаях изобара P = const пересекает изотерму в трех точках L, C, G (рис. 3.1). Изотерма содержит волнообразный участок LBCAG. Она сначала монотонно опускается вниз (участок DB), затем на участке BA монотонно поднимается вверх, а за точкой A снова монотонно опускается.

При некоторой промежуточной температуре три корня V₁, V₂, V₃ становятся равными. Такая температура и соответствующая ей изотерма называются критическими. Критическая изотерма FKH всюду монотонно опускается вниз, за исключением одной точки K, являющейся точкой перегиба изотермы. В ней касательная к изотерме горизонтальна. Точка K называется критической точкой. Соответствующие ей давление P_k , объем V_k и температура T_k называются также критическими. Говорят, что вещество находится в критическом состоянии, если его объем и давление (а следовательно, и температура) равны критическим.

Для нахождения критических параметров P_k, V_k, T_k учтем, что в критической точке уравнение (3.6) переходит в уравнение:

. (3.7)

Поскольку в этом случае все три корня совпадают и равны V_k , уравнение должно приводиться к виду:

. (3.8)

Возводя в куб и сравнивая коэффициенты уравнений (3.7) и (3.8), получим три уравнения:

.

Решая их, найдем выражения для параметров критического состояния вещества:

. (3.9)

К тем же результатам можно прийти, заметив, что критическая точка К является точкой перегиба изотермы, касательная в которой горизонтальна, а поэтому в точке К должны соблюдаться соотношения

.

Решая эти уравнения совместно с уравнением изотермы (3.4) придем к формулам (3.9).

Не все состояния вещества, совместимые с уравнением Ван-дер-Ваальса, могут быть реализованы в действительности. Для этого необходимо еще, чтобы они были термодинамически устойчивы. Одно из необходимых условий термодинамической устойчивости физически однородного вещества состоит в выполнении неравенства . Физически оно означает, что при изотермическом увеличении давления объем тела должен уменьшаться. Иными словами, при возрастании V все изотермы должны монотонно опускаться. Между тем, ниже критической температуры на изотермах Ван-дер-Ваальса имеются поднимающиеся участки типа BCA (рис. 3.1). Точки, лежащие на таких участках, соответствуют неустойчивым состояниям вещества, которые практически реализованы быть не могут. При переходе к практическим изотермам эти участки должны быть выброшены.

Таким образом, реальная изотерма распадается на две ветви EGA и BLD , отделенные друг от друга. Естественно предположить, что этим двум ветвям соответствуют различные агрегатные состояния вещества. Ветвь EA характеризуется относительно большими значениями объема или малыми значениями плотности, она соответствует газообразному состоянию вещества. Напротив, ветвь BD характеризуется относительно малыми объемами, а следовательно, большими плотностями, она соответствует жидкому состоянию вещества. Таким образом, уравнение Ван-дер-Ваальса распространяется и на область жидкого состояния. Таким путем удается получить удовлетворительное качественное описание явления перехода газа в жидкость и обратно.

Возьмем достаточно разреженный газ при температуре ниже критической. Исходное состояние его на диаграмме PV изображается точкой E (рис. 3.1). Будем сжимать газ квазистатически, поддерживая температуру T постоянной. Тогда точка, изображающая состояние газа, будет перемещаться по изотерме вверх. Можно было думать, что она достигает крайнего положения A , где изотерма обрывается. В действительности, однако, начиная с некоторой точки G , давление в системе перестает повышаться, и она распадается на две физически однородные части: газообразную и жидкую.

Процесс изотермического сжатия такой двухфазной системы изображается участком GL горизонтальной прямой. При этом во время сжатия плотности жидкости и газа остаются неизменными и равными их значениям в точках L и G соответственно. По мере сжатия количество вещества в газообразной фазе непрерывно уменьшается, а в жидкой фазе - увеличивается, пока не будет достигнута точка L, в которой все вещество перейдет в жидкое состояние.

Такой ход изотерм впервые был обнаружен на опыте в конце XVIII века голландским ученым Ван Марумом (1750-1837). Ван Марум провел серию опытов с целью проверки закона Бойля-Мариотта. Одним из исследуемых газов был аммиак. С увеличением давления объем газа сначала уменьшался обратно пропорционально давлению, как того требовал закон Бойля-Мариотта. Однако, когда давление достигло 7 атм., оно неожиданно перестало расти при дальнейшем сжатии, хотя объем и продолжал уменьшаться. При давлении 7 атм. произошло сжижение газообразного аммиака. Начиная с этого момента. сжатие вещества приводило лишь к увеличению количества жидкого и уменьшению газообразного аммиака.

После Ван Марума последовали многочисленные попытки путем сжатия газов перевести их в жидкое состояние. Особенно больших успехов в этом направлении достиг Фарадей (1791-1867). Он применял комбинированный метод, сочетая сжатие газа с его охлаждением. Однако все эти исследования производились вслепую. Оставалось неясно, почему при сжатии одних газов происходит сжижение, а других - нет. Влияние охлаждения и сама возможность сжижения газов не были ясны. Положение разъяснилось после классических работ английского физика Томаса Эндрюса (1813-1885), выполненных в течение 1861-1869 гг. Эндрюс систематически исследовал ход изотерм углекислоты (СО₂) при различных температурах и на основе этих исследований ввел понятие критической температуры. Углекислота им была выбрана сознательно, так как она обладает критической температурой (31ºС), лишь незначительно превышающей комнатную, и сравнительно невысоким критическим давлением (72,9 атм.). Оказалось, что при температуре выше 31ºС изотермы углекислоты монотонно опускаются вниз, т.е. имеют гиперболический вид. Ниже этой температуры на изотермах углекислоты появляются горизонтальные участки, на которых изотермическое сжатие газа приводит к его конденсации, но не к увеличению давления. Таким путем было установлено, что сжатием газ можно превратить в жидкость только тогда, когда его температура ниже критической.

При специальных условиях могут быть реализованы состояния, изображаемые участками изотермы GA и BL. Эти состояния называются метастабильными. Участок GA изображает так называемый пересыщенный пар, участок BL - перегретую жидкость. Обе фазы обладают ограниченной устойчивостью. Каждая из них может существовать до тех пор, пока она не граничит с другой более устойчивой фазой. Например, пересыщенный пар переходит в насыщенный пар, если в него ввести капли жидкости. Перегретая жидкость закипает, если в нее попадают пузырьки воздуха или пара.

Внутренняя энергия реального газа

Внутренняя энергия реального газа должна включать в себя, кроме кинетической энергии молекул, энергию взаимодействия между молекулами. Для нахождения внутренней энергии реального газа воспользуемся тем обстоятельством, что работа, совершаемая при расширении газа против сил взаимного притяжения молекул друг к другу, равна приращению энергии взаимодействия:

.

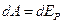Силы взаимного притяжения между молекулами учтены в уравнении (3.3) с помощью добавки к давлению . Соответственно работа против сил взаимодействия между молекулами может быть представлена в виде .

Таким образом,

.

Интегрирование этого выражения дает, что

. (3.10)

Внутренняя энергия реального газа U зависит как от объема, так и от температуры. Следовательно, выражение для U имеет вид:

(const из выражения (3.10) включена в f (Т)).

Это выражение в пределе, при стремление объема к бесконечности, должно переходить в выражение для внутренней энергии идеального газа. Следовательно, .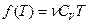

Итак, внутренняя энергия реального газа определяется формулой

. (3.11)

Эффект Джоуля - Томсона

Различают дифференциальный и интегральный эффекты Джоуля-Томсона. В технике для получения низких температур применяется интегральный эффект Джоуля-Томсона, но рассмотрение мы начнем с дифференциального эффекта или опытов Джоуля-Томсона (1852-1862 гг.). В этих опытах бралась цилиндрическая трубка, окруженная теплоизолирующим материалом. В середине трубки между двумя сетками MN и M₁N₁ (рис. 3.2) помещалась пробка из плотной ваты или очесов шелка. Исследуемый газ под действием разности давлений медленно протекал через пробку. В этих условиях в каждый момент времени газ по обе стороны пробки находился в термодинамически равновесных состояниях. Давления газа по разные стороны пробки P₁ и P₂ поддерживались постоянными. При стационарном течении по одну сторону пробки устанавливалась постоянная температура газа Т₁, по другую - постоянная температура Т₂. Эти температуры и измерялись в опыте. Изменение температуры газа при стационарном течении газа через пробку и называется эффектом Джоуля-Томсона.

Рис. 3.2. Дифференциальный эффект Джоуля-Томсона

Выделим мысленно по левую сторону пробки объем газа V₁ . После прохождения через пробку выделенная порция газа займет объем V₂. В левой части над газом производилась работа P₁V₁ , в правой части газ производит работу P₂V₂ . Полная работа, совершенная газом, равна . Применим к выделенной порции газа первое начало термодинамики. Теплоты газ не получал, так как стенки трубки теплоизолированы, физическое состояние пробки и ее внутренняя энергия остались неизменными. Поэтому

, или (3.12)

,

где - изменение внутренней энергии выделенной массы газа.

По определению, величина есть термодинамическая функция газа - энтальпия. Поэтому последнее равенство означает, что в опыте Джоуля-Томсона энтальпия газа не меняется, т.е. .

Это соотношение является основным в теории эффекта Джоуля-Томсона. Пусть по разные стороны пробки поддерживается малая разность давлений DP. Соответствующая ей разность температур DT измеряется в опыте. Течение газа предполагается установившимся. Задача теории состоит в том, чтобы, зная DP и уравнение состояния газа, вычислить DT. При первом чтении можно опустить дальнейшие выкладки и сразу перейти к формуле (3.19). Однако, вывод соотношения (3.19) представляет интерес с точки зрения дальнейшего знакомства с вычислениями в термодинамике.

Поскольку в опыте Джоуля-Томсона энтальпия H не меняется то, рассматривая ее как функцию температуры и давления, можно написать:

. (3.13)

По определению энтальпии

.

Для вычисления частной производной обратимся к первому началу термодинамики, записанному в виде:

. (3.14)

Используя определение энтальпии , перепишем уравнение (3.14) следующим образом:

, или

. (3.15)

Разделив выражение (3.15) на Т, получим приращение энтропии:

. (3.16)

Рассматривая энтропию как функцию параметров Т и Р, можно представить приращение энтропии в виде

.

Сравнение этого выражения с (3.16) дает, что

. (3.17)

Смешанные частные производные некоторой функции удовлетворяют условию:

.

В соответствии с этим:

.

Подстановка в это равенство выражений (3.17) приводит к соотношению:

.

Осуществив дифференцирование, получим:

.

Приняв во внимание, что , приходим к формуле

. (3.18)

Тогда уравнение (3.13) примет вид:

,

откуда следует

, (3.19)

где C_P- молярная теплоемкость газа при постоянном давлении.

При выводе (3.19) не предполагалось знания явного вида уравнения состояния газа. Для получения конкретных результатов надо знать уравнение состояния газа. Если газ идеальный, то для одного моля газа из уравнения Менделеева-Клапейрона имеем , и тогда , и из соотношения (3.19) следует , т.е. для идеального газа эффект Джоуля-Томсона не имеет места.

Но для реальных газов, вообще говоря, происходит либо нагревание, либо охлаждение. В качестве уравнения состояния реального газа возьмем уравнение Ван-дер-Ваальса:

, (3.20)

где a и b - константы Ван-дер-Ваальса.

Рассмотрим простейший случай разреженного газа, когда члены, содержащие a и b, являются малыми поправками. Можно ограничиться линейным приближением, отбросив все члены с высшими степенями a и b. В этом приближении соотношение (3.19) приводит к выражению

. (3.21)

Если 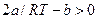, то и газ охлаждается. Если, напротив, , то и газ нагревается. В частности, при , газ всегда охлаждается; при , - всегда нагревается. Первый результат понятен, так как при расширении кинетическая энергия теплового движения газа расходуется на работу против сил молекулярного притяжения. Второй результат не столь очевиден.

При изменение температуры равно нулю. Температура называется температурой инверсии дифференциального эффекта Джоуля-Томсона. При T < T_i в опыте Джоуля-Томсона газ охлаждается, при T > T_i газ нагревается. Для большинства газов T_i лежит значительно выше комнатной температуры. Такие газы в опыте Джоуля-Томсона охлаждаются. Для водорода и гелия T_i лежит значительно ниже комнатной температуры (T_i = - 80ºC), и эти газы нагреваются.

Перейдем теперь к рассмотрению интегрального эффекта Джоуля-Томсона. Интегральный эффект Джоуля-Томсона получают, заставляя газ, находящийся под высоким давлением (порядка сотен атмосфер), перетекать в пространство с низким давлением (порядка атмосферного) через вентиль или узкое отверстие (рис. 3.3). Такой процесс называется дросселированием газа.

 

Изменение температуры газа T₂ - T₁ при интегральном эффекте определяется формулой:

. (3.22)

В зависимости от знака подынтегрального выражения изменение температуры T₂ - T₁ может быть как положительным, так и отрицательным. В частности, если во всем диапазоне давлений дифференциальный эффект приводит к DT < 0, то и интегральный эффект будет приводить к T₂ - T₁ < 0, т.е. в результате дросселирования газ должен охлаждаться. При комнатной температуре это имеет место для большинства газов, в частности, для воздуха и углекислоты. Совсем иначе ведет себя водород. Для него при комнатных температурах интегральный эффект Джоуля-Томсона приводит к нагреванию газа. Такое нагревание иногда приводит к катастрофам, в которых сильно сжатый водород самопроизвольно воспламеняется при истечении из поврежденных труб. При внезапном расширении водород может охлаждаться лишь тогда, когда его температура ниже минус 80ºС.