 |
|
Доказательство критерия Найквиста
Характеристическое уравнение замкнутой системы
 , ,
| (5.11) |
в которое входит передаточная функция условно разомкнутой системы
 . .
| (5.12) |
С учетом (5.12) уравнение (5.11) запишем в виде
 . .
| (5.13) |
Обозначим корни числителя через  ,
,  ,
,  , ...
, ...  , а корни знаменателя уравнения (5.13) через
, а корни знаменателя уравнения (5.13) через  ,
,  ,
,  , ...
, ...  . Тогда уравнение (5.13) можно представить как
. Тогда уравнение (5.13) можно представить как
 . .
| (5.14) |
При переходе к частотной функции заменой  получим
получим
 . .
| (5.15) |
На основании принципа аргумента при изменении  от
от  до
до  результирующая фаза будет равна сумме углов поворота всех векторов сомножителей числителя и знаменателя.
результирующая фаза будет равна сумме углов поворота всех векторов сомножителей числителя и знаменателя.
Для устойчивой замкнутой системы вектор числителя  повернется при изменении
повернется при изменении  от нуля до бесконечности на угол
от нуля до бесконечности на угол  .
.
Если система устойчива в разомкнутом состоянии, то вектор  также повернется на угол
также повернется на угол  . Результирующий угол поворота вектора
. Результирующий угол поворота вектора  будет равен разности углов поворота векторов
будет равен разности углов поворота векторов  и
и  . Тогда получим
. Тогда получим  , т.е. приращение аргумента результирующего вектора равно нулю.
, т.е. приращение аргумента результирующего вектора равно нулю.
С другой стороны, на основании (5.11)
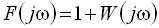 . .
| (5.16) |
 Рис. 5.5. К доказательству критерия Найквиста Рис. 5.5. К доказательству критерия Найквиста
|
Изобразим вектор  совместно с вектором
совместно с вектором  согласно уравнению (5.16) на комплексной плоскости а.ф.х. разомкнутой системы (рис. 5.5). Для устойчивой системы достаточно, чтобы а.ф.х. разомкнутой системы не охватывала точку с координатами
согласно уравнению (5.16) на комплексной плоскости а.ф.х. разомкнутой системы (рис. 5.5). Для устойчивой системы достаточно, чтобы а.ф.х. разомкнутой системы не охватывала точку с координатами  (только тогда результирующий угол поворота
(только тогда результирующий угол поворота  ).
).
Для случая, когда система в разомкнутом состоянии является неустойчивой и имеет 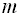 правых корней, то результирующий угол поворота вектора
правых корней, то результирующий угол поворота вектора  будет
будет
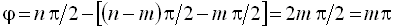 . .
| (5.17) |
Это означает, что для устойчивой системы а.ф.х. должна охватывать точку 
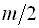 раз.
раз.
| 5.4. Алгебраический критерий устойчивости Гурвица |
Применительно к задачам теории управления критерий Гурвица можно сформулировать так: автоматическая система, которой соответствует характеристическое уравнение
 , ,
|
устойчива, если при  положительны все определители
положительны все определители  вида
вида
 . .
| (5.18) |
Если хотя бы один из определителей (5.18), называемых определителями Гурвица, отрицателен, то система неустойчива.
Определители (5.18) составляют следующим образом: на главной диагонали записывают все коэффициенты характеристического уравнения от  до
до  (в порядке возрастания индекса), затем в каждом столбце выше диагональных коэффициентов записывают коэффициенты с последовательно возрастающими индексами, а ниже – с последовательно убывающими индексами; на место коэффициентов с индексами большими
(в порядке возрастания индекса), затем в каждом столбце выше диагональных коэффициентов записывают коэффициенты с последовательно возрастающими индексами, а ниже – с последовательно убывающими индексами; на место коэффициентов с индексами большими  или меньшими нуля проставляют нули. При этом каждая
или меньшими нуля проставляют нули. При этом каждая 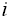 -я матрица получается квадратной размером
-я матрица получается квадратной размером  .
.
Так как последний столбец главного определителя  содержит всегда только один элемент
содержит всегда только один элемент  , отличный от нуля, то, согласно известному свойству определителей,
, отличный от нуля, то, согласно известному свойству определителей,
 . .
| (5.19) |
Если главный определитель  , а все остальные определители положительны, то система находится на границе устойчивости. С учетом выражения (5.19) это условие распадается на два:
, а все остальные определители положительны, то система находится на границе устойчивости. С учетом выражения (5.19) это условие распадается на два:
 и и  . .
| (5.20) |
Условию  соответствует один нулевой корень, т.е. апериодическая граница устойчивости, а условию
соответствует один нулевой корень, т.е. апериодическая граница устойчивости, а условию  – пара мнимых корней, т.е. колебательная граница устойчивости.
– пара мнимых корней, т.е. колебательная граница устойчивости.
Как показывает анализ, для устойчивости систем не выше четвертого порядка необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определитель  были положительными.
были положительными.
Критерий Гурвица следует применять для анализа систем не выше пятого порядка. При более высоком порядке систем вычисление определителей становится затруднительным без применения средств вычислительной техники.
Пример 1
Характеристическое уравнение замкнутой системы
 . .
|
Определить устойчивость системы
Решение. Все коэффициенты этого характеристического уравнения положительны, а определитель Гурвица 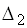 с четным индексом равен
с четным индексом равен
 . .
|
Система устойчива.
| 5.5. Построение областей устойчивости |
Определение областей устойчивости. Пусть все коэффициенты характеристического уравнения замкнутой системы
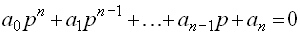
| (5.21) |
заданы, кроме одного, например,  . Допустим, что коэффициент
. Допустим, что коэффициент  изменяется от нуля до бесконечности. Будем придавать этому коэффициенту ряд значений и определять при этом значения всех
изменяется от нуля до бесконечности. Будем придавать этому коэффициенту ряд значений и определять при этом значения всех  корней характеристического уравнения. Если на некоторой вещественной полуоси отмечать для каждого значения
корней характеристического уравнения. Если на некоторой вещественной полуоси отмечать для каждого значения  точку, которой соответствует определенное распределение корней на комплексной плоскости, то выбранная полуось может быть разбита на ряд отрезков в зависимости от того, все или не все корни левые. На стыках таких отрезков один или несколько корней находятся на мнимой оси (рис. 5.6, а).
точку, которой соответствует определенное распределение корней на комплексной плоскости, то выбранная полуось может быть разбита на ряд отрезков в зависимости от того, все или не все корни левые. На стыках таких отрезков один или несколько корней находятся на мнимой оси (рис. 5.6, а).
Если в уравнении изменяются два коэффициента, то на плоскости этих коэффициентов, вычисляя все корни уравнения, можно выделить области устойчивости и неустойчивости (рис. 5.6, б).
Аналогично можно исследовать совокупность нескольких коэффициентов характеристического уравнения. Наиболее просто область устойчивости выделяется для уравнения  :
: 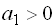 ,
,  (рис. 5.6, в).
(рис. 5.6, в).
Понятие о  -разбиении пространства коэффициентов характеристического уравнения Если при значениях каких-либо двух коэффициентов характеристического уравнения в плоскости корней имеется
-разбиении пространства коэффициентов характеристического уравнения Если при значениях каких-либо двух коэффициентов характеристического уравнения в плоскости корней имеется  корней левых и
корней левых и  корней правых, то, изменяя значения коэффициентов (например,
корней правых, то, изменяя значения коэффициентов (например,  и
и  ), получим определенную кривую на плоскости коэффициентов, ограничивающую область, каждая точка которой характеризует указанное расположение корней относительно мнимой оси. Эту область обозначим
), получим определенную кривую на плоскости коэффициентов, ограничивающую область, каждая точка которой характеризует указанное расположение корней относительно мнимой оси. Эту область обозначим  (рис. 5.7).
(рис. 5.7).
 Рис. 5.6. Зоны и области устойчивости Рис. 5.6. Зоны и области устойчивости
|
Число корней может иметь любое целое значение, поэтому в плоскости коэффициентов можно указать области  , соответствующие разным значениям
, соответствующие разным значениям  . Например, при степени
. Например, при степени  можно рассматривать области
можно рассматривать области  ;
;  ;
;  ;
;  ;
; 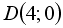 . Из этих областей только последняя является областью устойчивости.
. Из этих областей только последняя является областью устойчивости.
 Рис. 5.7. Области распределения корней Рис. 5.7. Области распределения корней
|
Разбиение пространства коэффициентов на области устойчивости и неустойчивости называется D-разбиением.
Мнимая ось в плоскости корней есть отображение границы  -разбиения в плоскости коэффициентов (рис. 5.7). Чтобы определить границу
-разбиения в плоскости коэффициентов (рис. 5.7). Чтобы определить границу  -разбиения, надо заменить в характеристическом уравнении
-разбиения, надо заменить в характеристическом уравнении  на
на  и изменять частоту от минус бесконечности до плюс бесконечности.
и изменять частоту от минус бесконечности до плюс бесконечности.
 -разбиение плоскости одного комплексного параметра. Если требуется оценить влияние на устойчивость только одного параметра, а значения остальных параметров заданы, целесообразно ввести вместо этого параметра комплексную величину, вещественная часть которой равна исследуемому параметру. Пусть параметр
-разбиение плоскости одного комплексного параметра. Если требуется оценить влияние на устойчивость только одного параметра, а значения остальных параметров заданы, целесообразно ввести вместо этого параметра комплексную величину, вещественная часть которой равна исследуемому параметру. Пусть параметр  входит в характеристическое уравнение
входит в характеристическое уравнение
 , или , или 
| (5.22) |
В качестве  может быть принята постоянная времени
может быть принята постоянная времени  или коэффициент усиления
или коэффициент усиления  любого звена системы. Полагаем временно, что
любого звена системы. Полагаем временно, что  – комплексное число. При подстановке
– комплексное число. При подстановке  из (5.15) получим
из (5.15) получим
 . .
| (5.23) |
Придавая различные значения  , строим кривую, отображающую мнимую ось комплексной плоскости корней, т. е. границу
, строим кривую, отображающую мнимую ось комплексной плоскости корней, т. е. границу  -разбиения (рис. 5.8).
-разбиения (рис. 5.8).
 Рис. 5.8. Граница D-разбиения Рис. 5.8. Граница D-разбиения
|
Кривую достаточно построить в пределах 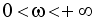 , а затем дополнить зеркальным отображением. Далее необходимо наметить предполагаемую область устойчивости
, а затем дополнить зеркальным отображением. Далее необходимо наметить предполагаемую область устойчивости  . Для этого применяют правило штриховки: границей в плоскости корней является мнимая ось, и при движении по ней от
. Для этого применяют правило штриховки: границей в плоскости корней является мнимая ось, и при движении по ней от  до
до  область корней устойчивой системы располагается слева. Соответственно этому в плоскости
область корней устойчивой системы располагается слева. Соответственно этому в плоскости  на D-кривой необходимо отметить направление движения в диапазоне частот
на D-кривой необходимо отметить направление движения в диапазоне частот  и также заштриховать левую часть кривой. Так как
и также заштриховать левую часть кривой. Так как  по физическому смыслу есть вещественная величина, то рассматриваются лишь те отрезки вещественной оси, которые лежат в области, окруженной внутренней штриховкой.
по физическому смыслу есть вещественная величина, то рассматриваются лишь те отрезки вещественной оси, которые лежат в области, окруженной внутренней штриховкой.
Для каждой области указывают распределение корней. Для этого полагают 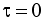 и находят корни характеристического уравнения
и находят корни характеристического уравнения 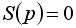 . Полученное распределение корней
. Полученное распределение корней  считают заданным и наносят на плоскость
считают заданным и наносят на плоскость  в области начала координат. Если в плоскости
в области начала координат. Если в плоскости  при движении от одной точки к другой пересекается D-кривая и при этом происходит переход с заштрихованной стороны на незаштрихованную, то в плоскости корней один корень пересекает мнимую ось. Если штриховка двойная (например, в точке пересечения кривых), то мнимую ось пересекают два корня. Так находится область плоскости
при движении от одной точки к другой пересекается D-кривая и при этом происходит переход с заштрихованной стороны на незаштрихованную, то в плоскости корней один корень пересекает мнимую ось. Если штриховка двойная (например, в точке пересечения кривых), то мнимую ось пересекают два корня. Так находится область плоскости  , соответствующая расположению всех корней в левой полуплоскости.
, соответствующая расположению всех корней в левой полуплоскости.
Далее выбирают из этой области какое-либо значение  и проверяют устойчивость по любому критерию.
и проверяют устойчивость по любому критерию.
Пример 2
Построить кривую  -разбиения для коэффициента усиления
-разбиения для коэффициента усиления  разомкнутой системы. Характеристическое уравнение замкнутой системы имеет вид
разомкнутой системы. Характеристическое уравнение замкнутой системы имеет вид
 . .
|
Изменяя  от
от  до
до  , определяем
, определяем  и
и  и строим
и строим  -кривую (рис. 5.9). Определим из исходного уравнения
-кривую (рис. 5.9). Определим из исходного уравнения  , заменим
, заменим 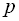 на
на  и выделим вещественную и мнимую части:
и выделим вещественную и мнимую части:

|
 . .
|
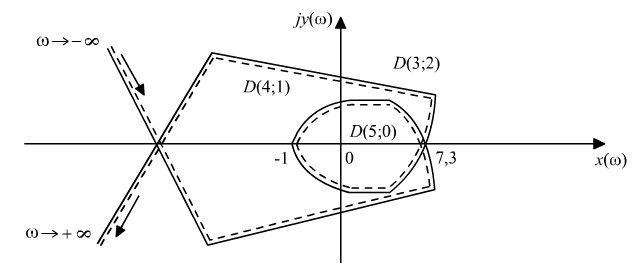 Рис. 5.9. D-кривая Рис. 5.9. D-кривая
|
В области с началом координат для любого значения  устанавливаем по любому из критериев устойчивости, что система устойчива. При переходе через линию с одинарной штриховкой прибавляется один правый корень.
устанавливаем по любому из критериев устойчивости, что система устойчива. При переходе через линию с одинарной штриховкой прибавляется один правый корень.