 |
|
Преобразования Лапласа
Исследование АСР существенно упрощается при использовании прикладных математических методов операционного исчисления, поскольку позволяет от решения ДУ перейти к решению алгебраических уравнений. Например, функционирование некоторой системы описывается ДУ вида
 , (2.1)
, (2.1)
где х и у - входная и выходная величины. Если в данное уравнение вместо x(t) и y(t) подставить функции X(s) и Y(s) комплексного переменного s такие, что
 и
и  , (2.2)
, (2.2)
то исходное ДУ при нулевых начальных условиях равносильно линейному алгебраическому уравнению
a2 s2 Y(s) + a1 s Y(s) + a0 Y(s) = b1 X(s) + b0 X(s).
Такой переход от ДУ к алгебраическому уравнению называется преобразованием Лапласа, формулы (2.2) соответственно формулами преобразования Лапласа, а полученное уравнение - операторным уравнением.
Новые функции X(s) и Y(s) называются изображениями x(t) и y(t) по Лапласу, тогда как x(t) и y(t) являются оригиналами по отношению к X(s) и Y(s).
Переход от одной модели к другой достаточно прост и заключается в замене знаков дифференциалов  на операторы sn, знаков интегралов
на операторы sn, знаков интегралов  на множители
на множители  , а самих x(t) и y(t) - изображениями X(s) и Y(s).
, а самих x(t) и y(t) - изображениями X(s) и Y(s).
Таблица 1.1 - Преобразования Лапласа
| Оригинал x(t) | Изображение X(s) |
| d-функция | |

| |
| t | 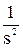
|
| t2 | 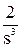
|
| tn | 
|
| e-at | 
|
| a.x(t) | a.X(s) |

| 
|
| x(t - a) | X(s).e-as |

| sn.X(s) |

| 
|
Таблица 1.2 - Формулы обратного преобразования Лапласа (дополнение)
| Изображение X(s) | Оригинал x(t) | |

| a Î R, M Î R (a и М - действительные числа) | M.e-at |
| a = a + j. w M = C + j.D (a и М – комплексные числа) | 2.ea*t.[C.cos(w.t) - D.sin(w.t)] для пары комплексных корней |
Для обратного перехода от операторного уравнения к функциям от времени используется метод обратного преобразования Лапласа. Общая формула обратного преобразования Лапласа:
 , (2.3)
, (2.3)
где f(t) - оригинал, F(jw) - изображение при s = jw, j - мнимая единица, w - частота.
Эта формула достаточно сложна, поэтому были разработаны специальные таблицы (см. таблицы 1.1 и 1.2), в которые сведены наиболее часто встречающиеся функции F(s) и их оригиналы f(t). Они позволяют отказаться от прямого использования формулы (2.3). Более полные таблицы преобразований Лапласа можно найти, например, в [22, 23].
Существует несколько теорем преобразования Лапласа.
Теорема 1. Теорема линейности. Изображение суммы функций равно сумме изображений, то есть, если f1 имеет изображение F1(s) (или более кратко f1 « F1(s) ), f2 « F2(s) и т.д., то
a1.f1 + a2.f2 + … + an.fn « a1.F1(s) + a2.F2(s) + … + an.Fn(s).
Теорема 2. Теорема дифференцирования. Если f(t) имеет изображение F(s), то при нулевых начальных условиях (т.е. при f(0) = 0, f’(0) = 0 и т.д.) производные f(t) будут иметь изображения:
f’(t) « s.F(s) – для первой производной,
f ”(t) « s2.F(s) – для второй производной,
f(n)(t) « sn.F(s) – для n-й производной.
При ненулевых начальных условиях:
f’(t) « s.F(s) – f(0) – для первой производной,
f ”(t) « s2.F(s) – s.f(0) – f’(0) – для второй производной,
f(n)(t) « sn.F(s) – sn-1.f(0) - sn-2.f’(0) - … - f(n-1)(0) – для n-й.
Теорема 3. Теорема смещения.
f(t).ea×t « F(s - a).
Например, если 1(t) «  (см. таблицу 1.1), то 1.ea×t «
(см. таблицу 1.1), то 1.ea×t «  .
.
Теорема 4. Теорема запаздывания.
f(t - t) « F(s) .e-t×s,
где t - запаздывание по времени.
Например, если 1(t) «  , то 1(t - t) «
, то 1(t - t) «  .
.
Теорема 5. Теорема интегрирования.
 .
.
Теорема 6. О начальных и конечных значениях.
 ,
,
 ,
,
где f(0) – начальное значение функции (при t = 0),
fуст – конечное (значение в установившемся режиме).
Закон изменения выходного сигнала обычно является функцией, которую необходимо найти, а входной сигнал, как правило, известен. Некоторые типовые входные сигналы были рассмотрены в п. 2.3. Здесь приводятся их изображения:
единичное ступенчатое воздействие имеет изображение X(s) =  ,
,
дельта-функция X(s) = 1,
линейное воздействие X(s) = 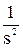 .
.
Пример. Решение ДУ с использованием преобразований Лапласа.

Допустим, входной сигнал имеет форму единичного ступенчатого воздействия, т.е. x(t) = 1. Тогда изображение входного сигнала, согласно таблице 1.1, имеет вид X(s) =  .
.
Производим преобразование исходного ДУ по Лапласу и подставляем X(s):
s2×Y(s) + 5×s×Y(s) + 6×Y(s) = 2×s×X(s) + 12×X(s),
s2×Y(s) + 5×s×Y(s) + 6×Y(s) = 2×s  + 12
+ 12  ,
,
Y(s)×(s3 + 5s2 + 6s) = 2×s + 12.
Определяется выражение для Y:
 .
.
Оригинал полученной функции отсутствует в таблице оригиналов и изображений. Для решения задачи его поиска дробь разбивается на сумму простых дробей с учетом того, что знаменатель может быть представлен в виде s(s + 2)(s + 3):
 =
=  =
=  -
- 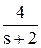 +
+  .
.
Теперь, используя табличные функции (см. таблицы 1.1 и 1.2), определяется оригинал выходной функции:
y(t) = 2 - 4.e-2t + 2.e-3t. ¨
При решении ДУ с использованием преобразований Лапласа часто встает промежуточная задача разбиения дроби на сумму простых дробей. Существуют два пути решения этой задачи:
- путем решения системы уравнений относительно коэффициентов числителей,
- путем расчета коэффициентов числителей по известным формулам.
Общий алгоритм разбиения дроби на сумму простых дробей:
шаг 1 – определяются корни знаменателя si (знаменатель дроби приравниватся к нулю и решается полученное уравнение относительно s);
шаг 2 – каждому корню ставится в соответствие простая дробь вида 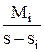 , где Мi – неизвестный коэффициент; если имеет место кратный корень с кратностью k, то ему ставится в соответствие k дробей вида
, где Мi – неизвестный коэффициент; если имеет место кратный корень с кратностью k, то ему ставится в соответствие k дробей вида  ;
;
шаг 3 – определяются коэффициенты Mi по одному из вариантов расчета.
Первый вариант. Определение Mi с помощью системы уравнений.
Все дроби приводятся к одному знаменателю, затем путем сравнения коэффициентов при равных степенях s числителя полученной дроби и числителя исходной определяется система из n уравнений, где n – степень знаменателя (количество корней si и коэффициентов Mi). Решение системы относительно Mi дает искомые коэффициенты.
Пример. Декомпозиция дроби из предыдущего примера. В исходной дроби n = 3, поэтому решение уравнения s3 + 5s2 + 6s = 0 дает 3 корня: s0 = 0, s1 = -2 и s2 = -3, которым соответствуют знаменатели простых дробей вида s, (s – s1) = (s + 2) и (s – s2) = (s + 3). Исходная дробь декомпозируется на три дроби:
 =
=  =
=  +
+  +
+  .
.
Далее дроби приводятся к общему знаменателю:
=  .
.
Сравнивая получившуюся дробь с исходной, можно составить систему из трех уравнений с тремя неизвестными (при 2-й степени s в исходной дроби стоит 0, при 1-й стоит 2, свободный член равен 12):

 М0 + М1 + М2 = 0 M0 = 2
М0 + М1 + М2 = 0 M0 = 2
5.М0 + 3.М1 + 2.М2 = 2 à M1 = -4
6.М0 = 12 M2 = 2
Следовательно, дробь можно представить как сумму трех дробей:
 =
=  -
- 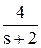 +
+  .¨
.¨
Второй вариант. Определение коэффициентов Mi по формулам.
Также как и в 1-м варианте необходимо найти корни знаменателя исходной дроби вида 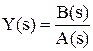 . Для определения Mi существуют формулы для каждого вида корней:
. Для определения Mi существуют формулы для каждого вида корней:
- Для нулевого корня si = 0 знаменатель исходной дроби можно записать в виде A(s) = s.A1(s); тогда коэффициент Mi можно определить как  .
.
- Для ненулевого некратного корня (действительного или комплексного) si:
 ,
,
где A’(s) – производная знаменателя по s.
Примечание - Комплексные корни при решении уравнений появляются комплексно-сопряженными парами вида si = ai ± j×wi , где ai – действительныя часть корня, wi – мнимая часть, j – мнимая единица. Поэтому коэффициенты для этих корней также будут комплексно-сопряженными: Mi = ci ± di. То есть достаточно определить коэффициент только для одного корня, для парного корня он будет комплексно-сопряженным.
- Для корня si кратности k исходная дробь может быть представлена в виде
 ;
;
данному корню соответствуют k дробей вида
 ,
,
коэффициенты которых определяются по формуле
 .
.
Пример. Декомпозиция дроби. Рассматривается та же дробь, имеющая три корня: s0 = 0, s1 = -2 и s2 = -3.
Для корня s0 = 0 имеем B(s) = 2.s + 12, A1(s) = s2 + 5s + 6 ,
 .
.
Для корня s1 = -2 имеем A’(s) = 3.s2 + 10.s + 6 и
 .
.
Для корня s2 = -3 имеем аналогично
 .
.
Видно, что коэффициенты Mi, полученные разными методами, совпадают.¨
Пример.Случай обратного преобразования Лапласа при наличии комплексных корней.
Изображение выходного сигнала имеет вид
 .
.
Корни знаменателя включают нулевой корень, действительный и пару комплексных корней: s0 = 0; s1 = - 2,54; s2,3 = - 0,18 ± j*1,20.
Изображение Y(s) разбивается на сумму четырех дробей:
 .
.
Тогда оригинал y(t), согласно таблицам 1.1 и 1.2, имеет вид
y(t) = y0(t) + y1(t) + y2,3(t) = M0 +  + 2 еat [C . cos(w.t) - D . sin(w.t)],
+ 2 еat [C . cos(w.t) - D . sin(w.t)],
где a и w - действительная и мнимая части пары комплексных корней s2,3, C и D – действительная и мнимая части пары коэффициентов М2 и М3.
Для корня s0 = 0:
 ,
,
 ,
,
y0(t) = M0 = 0,85.
Для корня s1 = -2,54:
 ,
,
 ,
,
 ,
,
y1(t) =  .
.
Для корней s2,3 = -0,18 ± j*1,20:
 ,
,
 ,
,
 ,
,
y2,3(t) =2 е-0,18t [-0,34 cos(1,20 t) - 0,24 sin(1,20 t)].
В итоге получаем оригинал:
y(t) = 0,85 – 0,18 е-2,54 t – 2 е-0,18 t [0,34 cos(1,20 t) + 0,24 sin(1,20 t)].¨