 |
|
КОНТРОЛЬНАЯ РАБОТА №2
7.Классическим методом найти частное решение системы дифференциальных уравнений 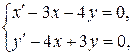 удовлетворяющее начальным условиям
удовлетворяющее начальным условиям  .
.
Решение. Решением этой системы является пара функций 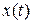 ,
, 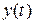 , удовлетворяющих системе, причем
, удовлетворяющих системе, причем  .
.
Продифференцируем первое уравнение по переменной  :
:
 .
.
Из первого уравнения определяем  , следовательно, из второго уравнения имеем
, следовательно, из второго уравнения имеем
 .
.
Подставляем  в уравнение, полученное после дифференцирования, приходим к уравнению
в уравнение, полученное после дифференцирования, приходим к уравнению
 ,
,
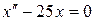 – линейное дифференциальное уравнение II порядка с
– линейное дифференциальное уравнение II порядка с
постоянными коэффициентами.
Составляем характеристическое уравнение и находим его корни:

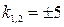 – действительные различные корни.
– действительные различные корни.
В этом случае общее решение дифференциального уравнения имеет вид
 ,
,
 .
.
Ранее определили  . Тогда
. Тогда
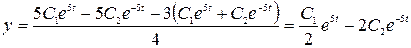 .
.
Общее решение системы 
Находим значения произвольных постоянных, используя начальные условия  :
:
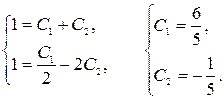
Частное решение системы 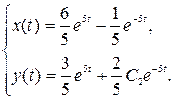
8. Вычислить определённый интервал с точностью до 0,001 путём разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.

Решение.
Разложим подынтегральную функцию в степенной ряд по формуле
 Тогда
Тогда





Полученный знакочередующийся ряд удовлетворяет условиям теоремы Лейбница. Так как четвёртый его член по абсолютной величине меньше 0,001, то для обеспечения заданной точности достаточно взять первые три члена ряда. Получаем:
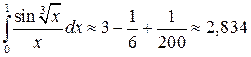 .
.
.
9. Разложить заданную функцию  в ряд Фурье по синусам на отрезке
в ряд Фурье по синусам на отрезке 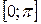 .
.
Решение. Так как по условию ряд должен содержать только синусы кратных углов, то следует продолжить заданную функцию на отрезок  нечетным образом, затем продолжить на всю числовую ось с периодом
нечетным образом, затем продолжить на всю числовую ось с периодом  . Теперь разложим полученную периодическую функцию в ряд Фурье (эта операция разложения называется гармоническим анализом) вида:
. Теперь разложим полученную периодическую функцию в ряд Фурье (эта операция разложения называется гармоническим анализом) вида:
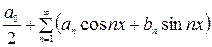 .
.
Так как заданная функция нечетная, то коэффициенты ряда Фурье  , а
, а  вычисляем по формуле
вычисляем по формуле

и ряд Фурье имеет вид  .
.
Подставляя заданную функцию, получаем
 .
.
Последний интеграл вычисляем методом интегрирования по частям, полагая  . Отсюда
. Отсюда  . следовательно,
. следовательно,


Таким образом, искомое разложение имеет вид

или

10. Дана функция двух переменных  . Найти:
. Найти:
1) экстремум функции 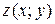 ;
;
2)  в точке А(1; –2);
в точке А(1; –2);
3) наибольшую скорость возрастания 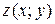 точке А(1; –2).
точке А(1; –2).
Решение. 1) Для отыскания экстремума функции 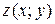 предварительно найдем частные производные первого и второго порядка:
предварительно найдем частные производные первого и второго порядка:

Приравняем их к нулю и решим систему уравнений:

Решением системы является точка М(–4; 1). Точка М(–4; 1) называется подозрительной на экстремум. Найдем частные производные второго порядка в точке М:

Из них составим определитель второго порядка

Так как  , то в точке М(–4; 1) есть экстремум. Производная
, то в точке М(–4; 1) есть экстремум. Производная  , а, значит, это точка минимума функции.
, а, значит, это точка минимума функции.
2) Градиент функции  найдем по формуле:
найдем по формуле:
 ,
,  и
и  были найдены в пункте 1.
были найдены в пункте 1.
 .
.
Градиент функции  в точке А(1; –2):
в точке А(1; –2):
 .
.
3) Наибольшая скорость возрастания функции равна модулю градиента:
 .
.
11.Вычислить массу неоднородной пластинки треугольной формы с вершинами в точках О (0;0) , А (5;0) , В (0;7) , поверхностная плотность которой в точке М (х;у) равна  .
.
Решение.
Изобразим пластинку на плоскости xOy.
 у
у
 В
В
 0 А х
0 А х
Масса неоднородной пластинки выражается через двойной интеграл по формуле:  .
.
В нашем случае область D - треугольник ОАВ,  .
.
Запишем уравнение прямой АВ, используя уравнение прямой в отрезках:
 , откуда получаем
, откуда получаем 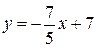 ; область D задаётся как решение системы неравенств
; область D задаётся как решение системы неравенств 
Вычислим массу m , переходя от двойного к повторному интегралу:




12. а) (Только для профиля ТСА.)Вычислить работу, совершаемую переменной силой  по прямой, соединяющей точки М(1; 1) и N(2; 3) .
по прямой, соединяющей точки М(1; 1) и N(2; 3) .
б) (Только для профилей ЭОЭТ и ЭОП.) Проверить, что векторное поле  потенциально; найти потенциал поля и работу, совершаемую силой
потенциально; найти потенциал поля и работу, совершаемую силой 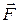 при переходе из точки М(1; 2) в точку N(3; 5).
при переходе из точки М(1; 2) в точку N(3; 5).
Решение. а) Для того чтобы найти работу, совершаемую переменной силой  , вычислим криволинейный интеграл
, вычислим криволинейный интеграл

по прямой, соединяющей точки М(1; 1) и N(2; 3).
Запишем уравнение прямой, проходящей через две данные точки:
 .
.
После преобразований получаем:  , поэтому
, поэтому  .
.
Перейдем от криволинейного интеграла к определенному, подставляя полученные нами выражения для y и dy и учитывая, что  .
.
Тогда работа A примет вид

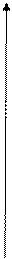 у
у
N
 3
3
1 M
 |
0 1 2 х
б) Векторное поле имеет вид  . Поэтому
. Поэтому
 ,
,  . Найдем частные производные
. Найдем частные производные  .
.
Производные совпадают, откуда следует, что поле 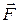 потенциально.
потенциально.
Потенциал векторного поля  находим по формуле
находим по формуле
 .
.
Для нашего случая
 ,
,
то есть потенциал данного поля равен
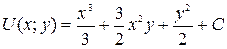 .
.
Проверим, правильно ли мы нашли потенциальную функцию. Для этого должны выполняться следующие условия:
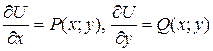 .
.
В нашем случае:
 по условию
по условию 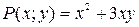 ,
,
 по условию
по условию  .
.
В потенциальных полях работа A силы 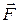 равна разности потенциалов, то есть
равна разности потенциалов, то есть  .
.
В нашем случае
 .
.
13.Найти вероятность безотказной работы участка цепи, если известно, что каждый  -ый элемент работает независимо от других с вероятностью
-ый элемент работает независимо от других с вероятностью 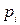 (
(  = 1, 2, 3, 4, 5, 6).
= 1, 2, 3, 4, 5, 6).  .
.
| |
| |
| |
 |
Решение. Участок цепи будет работать безотказно, если работают блоки 1–2 и 3–4–5–6 (последовательное соединение).
Рассмотрим блок 1–2. Элементы 1 и 2 соединены параллельно, следовательно, блок 1–2 будет работать, если хотя бы один из элементов 1, 2 исправен.
 – надежность блока 1–2.
– надежность блока 1–2.
Рассмотрим блок 3–4–5–6. Блок 3–4–5–6 будет безотказно работать хотя бы в одном из случаев:
исправны элементы 3 и 4,
исправен элемент 5,
исправен элемент 6.
 – вероятность безотказной работы блока 3–4.
– вероятность безотказной работы блока 3–4.
 –
–
надежность блока 3–4–5–6.
Следовательно,
 – искомая надежность участка цепи.
– искомая надежность участка цепи.
14.Измерены диаметры  для 90 деталей, обрабатываемых на некотором станке. Данные замеров приведены в табл. 1.
для 90 деталей, обрабатываемых на некотором станке. Данные замеров приведены в табл. 1.
Таблица 1
| 70,88 | 67,04 | 69,20 | 66,24 | 64,80 | 71,52 | 67,52 | 68,96 | 67,36 | 68,64 |
| 67,12 | 66,96 | 69,04 | 66,00 | 66,00 | 64,88 | 65,84 | 67,52 | 65,68 | 70,00 |
| 70,80 | 66,32 | 67,40 | 66,08 | 69,76 | 68,01 | 65,76 | 69,20 | 65,60 | 66,72 |
| 67,44 | 67,72 | 68,72 | 64,00 | 66,32 | 68,21 | 70,96 | 67,76 | 66,88 | 69,12 |
| 65,84 | 64,88 | 69,46 | 68,48 | 65,04 | 70,00 | 70,16 | 68,72 | 67,04 | 69,36 |
| 66,48 | 68,20 | 64,72 | 70,40 | 67,76 | 69,28 | 71,20 | 67,90 | 66,80 | 70,24 |
| 69,15 | 67,68 | 69,36 | 67.46 | 65,48 | 66,98 | 71,40 | 68,15 | 68,88 | 65,26 |
| 64,71 | 68,36 | 67,13 | 66,18 | 68,19 | 67,05 | 68,90 | 68,72 | 69,21 | 68,14 |
| 66,99 | 64,44 | 68,05 | 69,40 | 70,01 | 68,76 | 67,70 | 70,00 | 71,32 | 70,46 |
Выполнить статистическую обработку результатов измерений по следующему плану.
1) Построить вариационный ряд.
2) Найти точечные оценки математического ожидания (генеральной средней  ) и дисперсии
) и дисперсии 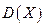 случайной величины ( признака)
случайной величины ( признака)  .
.
3) Построить гистограмму относительных частот.
4) На том же чертеже построить кривую нормального распределения и провести анализ соответствия выборочных данных нормальному закону распределения случайной величины Х.
Решение.
1) Для того чтобы построить вариационный ряд, сначала находят  ,
,  и размах вариационного ряда
и размах вариационного ряда  , затем определяют число интервалов
, затем определяют число интервалов  по формуле
по формуле  с округлением до ближайшего целого числа. В нашем случае
с округлением до ближайшего целого числа. В нашем случае  . Возьмём
. Возьмём  . Длина каждого интервала вычисляется по формуле
. Длина каждого интервала вычисляется по формуле  . Число
. Число 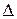 всегда округляют с избытком.
всегда округляют с избытком.
В рассматриваемом примере  Положим
Положим  .
.
Границы интервалов последовательно вычисляют по формулам  .
.
Для каждого i-го интервала подсчитывают количество  попавших в него данных
попавших в него данных  . Если выборочное данное совпадает с границей двух соседних интервалов, то его следует отнести к интервалу с меньшим номером. Затем вычисляют относительные частоты
. Если выборочное данное совпадает с границей двух соседних интервалов, то его следует отнести к интервалу с меньшим номером. Затем вычисляют относительные частоты 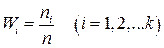 . Таким образом, получаем вариационный ряд (см. таблицу 2).
. Таким образом, получаем вариационный ряд (см. таблицу 2).
Таблица 2.
| № интервала | интервалы | Частоты 
| 
|
| (64,00 ; 65,08) (65,08 ; 66,16) (66,16 ; 67,24) (67,24 ; 68,32) (68,32 ; 69,40) (69,40 ; 70,48) (70,48 ; 71,56) |      8 8
       11 11
       14 14
             20 20
           17 17
         16 16
 4 4
| 






|
2) В качестве оценки математического ожидания (генеральной средней) берётся среднее арифметическое выборочных данных  .
.
За оценку дисперсии берётся исправленная выборочная дисперсия
 , где
, где  .
.
Этими формулами пользуются в случае небольшого объёма выборки ( 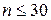 ). При выполнении расчётов при большом объёме выборки, то есть когда уже построен вариационный ряд
). При выполнении расчётов при большом объёме выборки, то есть когда уже построен вариационный ряд  вычисляется по формуле
вычисляется по формуле
 , (1)
, (1)
где  - середина i-го интервала. Исправленная дисперсия
- середина i-го интервала. Исправленная дисперсия 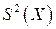 вычисляется по формуле
вычисляется по формуле  , где
, где
 . (2)
. (2)
Вычисления по формулам (1) и (2), как правило, сложны, поэтому для упрощения расчётов переходят от величин  к величинам
к величинам  по формуле
по формуле
 .
.
Величину  выберем следующим образом:
выберем следующим образом:
 , если
, если 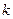 – четное,
– четное,
 , если
, если 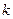 – нечетное.
– нечетное.
При таком выборе формулы перехода величины  будут принимать последовательные целые значения, близкие к нулю (см. таблицу 3).
будут принимать последовательные целые значения, близкие к нулю (см. таблицу 3).
Таблица 3.

| 
| 
| 
| 
| 
| 
|
| 64,540 65,620 66,700 67,780 68,860 69,940 71,020 | -3 -2 -1 | -24 -22 -14 | 0,08 0,11 0,15 0,20 0,18 0,17 0,04 | 0,04 0,10 0,18 0,22 0,19 0,12 0,05 | ||

|
В нашем случае С=  =67,78, вычисляем
=67,78, вычисляем  ,
,
 ,
,  ; затем по формулам
; затем по формулам
 ,
,  ,
,
найдём 

3) Гистограммой относительных частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы длиной 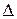 , расположенные на оси Ох, а высоты равны
, расположенные на оси Ох, а высоты равны  .
.
Соединив середины верхних сторон прямоугольников плавной линией, получим аналог плотности распределения случайной величины  (график эмпирической плотности распределения).
(график эмпирической плотности распределения).
4) По виду кривой эмпирического распределения (« колоколообразная» кривая) можно предположить, что случайная величина  распределена по нормальному закону. Для сравнения в той же системе координат построим кривую плотности нормального распределения:
распределена по нормальному закону. Для сравнения в той же системе координат построим кривую плотности нормального распределения:
 , где
, где 
Мы использовали значения, полученные во втором пункте.
В случае нормального распределения величины  вероятность того, что отклонение
вероятность того, что отклонение  от
от  окажется больше, чем величина
окажется больше, чем величина  , должна быть очень мала, близка к нулю. Это означает, что практически почти все значения выборочных данных должны попасть в интервал
, должна быть очень мала, близка к нулю. Это означает, что практически почти все значения выборочных данных должны попасть в интервал  , в нашем случае - в интервал (62,53 ; 73,27).
, в нашем случае - в интервал (62,53 ; 73,27).
Так как в рассматриваемом примере все выборочные значения попадают в указанный интервал, то есть основание считать, что случайная величина  распределена по нормальному закону с плотностью вероятности
распределена по нормальному закону с плотностью вероятности  . Для сравнения построим график этой функции, предварительно вычислив значения этой функции в точках
. Для сравнения построим график этой функции, предварительно вычислив значения этой функции в точках  (см. последний столбец таблицы 3). Найдём также максимум этой функции:
(см. последний столбец таблицы 3). Найдём также максимум этой функции:  3.
3.


ПРИЛОЖЕНИЯ


Продолжение таблицы значений функции Ф(х)

ОГЛАВЛЕНИЕ
| Таблицы вариантов……………………………………………………………… | |
| Задания для контрольных работ. Контрольная работа №1…………………... | |
| Контрольная работа №2………………………………………………………… | |
| Решение типовых примеров. Контрольная работа №1….……………………. | |
| Решение типовых примеров. Контрольная работа №2….……………………. | |
| Приложения……………………………………………………………………… |