 |
|
Предел и непрерывность функции
Задание 1
Найти пределы функций.
| 1. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
| 2. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
| 3. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
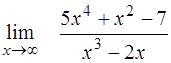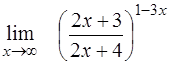| 4. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
| 5. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
| 6. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
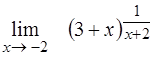| 7. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
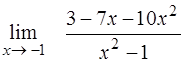| 8. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
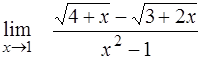| 9. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
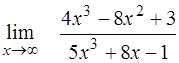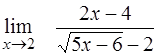| 10. | ¨  ;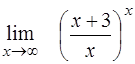
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
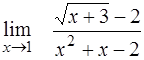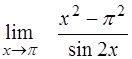| 11. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
| 12. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
| 13. | ¨  ;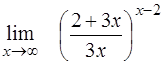
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
| 14. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
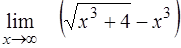| 15. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨ .
| |
| 16. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
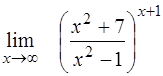| 17. | ¨  ;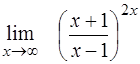
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
| 18. | ¨  ;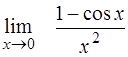
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
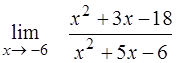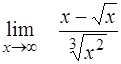| 19. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
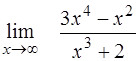| 20. | ¨  ;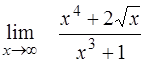
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
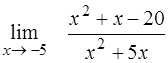| 21. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
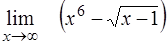| 22. | ¨ ;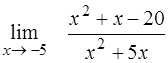
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
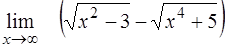| 23. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
| 24. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
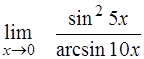| 25. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
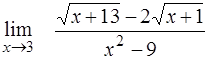| 26. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
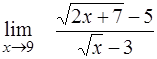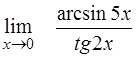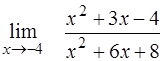| 27. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
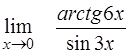| 28. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
| 29. | ¨  ;
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
| |
| 30. | ¨  ;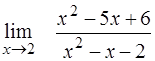
| ¨  ;
|
¨  ;
| ¨  ;
| |
¨  ;
| ¨  .
|
Задание 2
Исследовать функцию на непрерывность. Найти точки разрыва функции, если они существуют. Сделать чертеж функции.
1. 
| 11. 
|
2. 
| 12. 
|
3. 
| 13. 
|
4. 
|
14. 
|
5. 
| 15. 
|
6. 
| 16. 
|
7. 
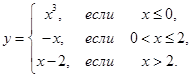
| 17. 
|
8. 
| 18. 
|
20. 
| 19. 
|
10. 
| 20. 
|
Примеры решения заданий
Предел и непрерывность функции
Практически предел функции находят не на основании определения предела функции, а на основании теорем о пределе функции.
Теорема. Если при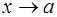 
существуют пределы функций 
и 
, то:
1. 
;
2. 
;
3. 
, где 
;
4. 
, где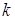 
- постоянный множитель.
Пример 7.Вычислить 
.
Решение. Так как
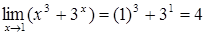, а 
,
то по теореме о пределе частного получаем, что 
.
Но не всегда можно применять теоремы о пределах без предварительного преобразования функций, стоящих под знаком предела. При этом возможны следующие неопределенные ситуации: 
, 
, 
, 
, 
.
Приемом раскрытия неопределенности вида является деление числителя и знаменателя на наивысшую степень x.
При неопределенности вида 
требуется выполнить преобразование функции, выделив в числителе и знаменателе дроби множитель, стремящийся к нулю. Затем сократить дробь на этот общий множитель.
Неопределенности же вида и путем преобразований приводят к одному из рассмотренных случав 
или 
. Поясним сказанное на примерах.
Пример 8. Вычислить 
.
Решение. Наивысшая степень x вторая, делим числитель и знаменатель на 
. Получим
, так как 
и 
.
Пример 9. Вычислить 
.
Решение. Имеет место неопределенность вида . Разложим числитель и знаменатель дроби на множители. Получим
.
Пример 10. Вычислить 
.
Решение. Числитель и знаменатель дроби при 
стремятся к нулю. Преобразуем функцию, выделим общий множитель
.
Пример 11. Вычислить 
.
Решение. Так как 
, а 
, то имеет место неопределенность вида 
.
Выполним преобразования
.
Пример 12. Найти точки разрыва функции.
если 
Решение. На интервалах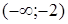 
, 
и 
функция непрерывна. Проверке подлежат только точки 
и 
.
Для того чтобы убедиться, что функция непрерывна в точке, требуется проверить, равны ли между собой односторонние пределы и равны ли они значению функции в этой точке.
Рассмотрим точку . 
.
Вычислим односторонние пределы
, 
.
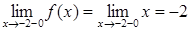Так как односторонние пределы не совпадают, - точка разрыва функции.
Рассмотрим точку . 
,
, 
,
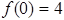- точка непрерывности функции, выполнены все условия непрерывности.
- точка непрерывности функции, выполнены все условия непрерывности (рис. 5).
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
ОСНОВНАЯ ЛИТЕРАТУРА
1. Индивидуальные задания по высшей математике. Часть 1. Под общ.ред. А.П.Рябушко. – Минск :Вышэйшая школа,2007. – 367 с.
2. Мацкевич И.П., Свирид Г.П., Булдык Г.М. Сборник задач и упражнений по высшей математике. Мн., Вышэйшая школа. 1996.
Унсович А.Н Высшая математика Учебно-методический комплекс для студентов экономических и инженерно-экономических специальностей. / Барановичский гос. университет. — Барановичи: БарГУ. — 2006. — Ч 1—368с
Унсович А.Н Учебно-методический комплекс для студентов экономических и инженерно-экономических специальностей. / Барановичский гос. университет. — Барановичи: БарГУ. — 2006. — Ч2—192с
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Гусак А.А. Пособие к решению задач по высшей математике. Мн., Издательство БГУ им. Ленина. 1973.
2. Кудрявцев Л.Д. Краткий курс математического анализа. - М.: Наука, 1989.
3. Русак. В. и др. Курс высшей математики: Алгебра и начала анализа. Анализ функции одной переменной. М., Высшая школа. 1994.
4. Справочник по высшей математике / А.А. Гусак, Г.М. Гусак, Е.А. Бричкова. -Минск: ТетраСистемс, 2006. - 640с.
5. ШипачёвВ.С. Высшая математика / Под ред. акад. А.Н.Тихонова. - М.: Высшая школа, 1985. -471с.