 |
|
Исследование поведения функций
Задание 1
Найти производные  данных функций.
данных функций.
1. а) 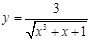 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
2. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
3. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
4. а)  ; б)
; б) 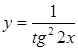 ;
;
в)  ; г)
; г)  .
.
5. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
6. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
7. а) 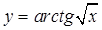 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
8. а) 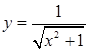 б)
б)  ;
;
в)  ; г)
; г)  .
.
9. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
10.а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
11.а) 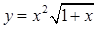 ; б)
; б)  ;
;
в)  ; г)
; г) 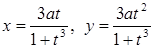 .
.
12.а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
13.а) 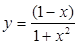 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
14.а)  ; б)
; б) 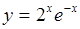 ;
;
в)  ; г)
; г)  .
.
15.а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
16.а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
17.а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
18.а)  ; б)
; б) 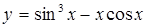 ;
;
в)  ; г)
; г)  .
.
19.а)  ; б)
; б)  ;
;
в) 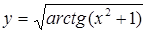 ; г)
; г)  .
.
20.а)  ; б)
; б)  ;
;
в)  ; г)
; г) 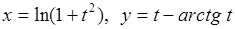 .
.
Задание 2
Найти интервалы монотонности и экстремумы функции.
1.  ; ;
| 11.  ; ;
|
2.  ; ;
| 12.  ; ;
|
3.  ; ;
| 13.  ; ;
|
4. 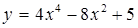 ; ;
| 14.  ; ;
|
5.  ; ;
| 15.  ; ;
|
6.  ; ;
| 16.  ; ;
|
7.  ; ;
| 17. 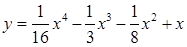 ; ;
|
8.  ; ;
| 18.  ; ;
|
9.  ; ;
| 19.  ; ;
|
10. 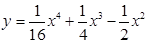 ; ;
| 20.  ; ;
|
Примеры решения заданий
Производная
Пример 1. Пользуясь формулами дифференцирования, найти производные следующих функций:


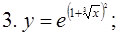 4.
4. 
Решение.
1. 
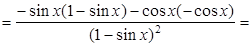

2.  есть сложная функция.
есть сложная функция.
 , где
, где  .
.
Производная сложной функции имеет вид
 или
или  .
.
Следовательно,
 .
.
 - сложная функция.
- сложная функция.
 , где
, где  , а
, а  ,
,
 . 4.
. 4.
4. 
Функция  от независимой переменной
от независимой переменной  задана через посредство вспомогательной переменной (параметра t). Производная от
задана через посредство вспомогательной переменной (параметра t). Производная от  по
по  определяется формулой
определяется формулой
 .
.
Находим производные от  и
и  по параметру t:
по параметру t:
 ,
, 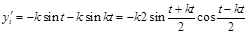 ,
,
 .
.
Пример 2. Составить уравнение касательной и нормали к кривой  в точке, где
в точке, где  .
.
Решение. Уравнение касательной к кривой в точке 
 ,
,
 ,
,  .
.
Для определения углового коэффициента касательной  находим производную
находим производную
 ,
,
 .
.
Подставляя значения  в уравнение, получим
в уравнение, получим
 или
или  .
.
Уравнение нормали
 ,
,
 или
или  .
.
Пример 3. Точка совершает прямолинейное колебательное движение по закону  . Определить скорость и ускорение движения в момент времени
. Определить скорость и ускорение движения в момент времени 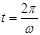 .
.
Решение. Найдем скорость  и ускорение а движения в любой момент времени t
и ускорение а движения в любой момент времени t
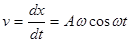 ;
;  .
.
При 
 ,
,  .
.
Дифференциал, производные высших порядков
Пример 1. Найти дифференциалы функций
1.  ; 2.
; 2.  ,
,
вычислить  .
.
Решение. Находим производную данной функции и, умножив ее на дифференциал независимой переменной, получим искомый дифференциал данной функции:
1.  ;
;
2. 
 .
.
Свойства дифференцируемых функций
Пример. Найти пределы используя правило Лопиталя.
1. 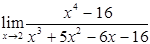 ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  .
.
Решение. Убедившись, что имеет место неопределенность  или
или  , применяем затем правило Лопиталя.
, применяем затем правило Лопиталя.
1. 

 ;
;
2. 



 ;
;
здесь правило Лопиталя применено дважды.
3. 


 ;
;
4.  .
.
Исследование поведения функций
Пример 1. Исследовать и построить график функции
 .
.
Решение.
1. Заданная функция определена и непрерывна на всей числовой оси
 .
.
2. Функция нечетная, ибо 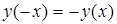 , ее график будет симметричен относительно начала координат. Поэтому достаточно построить график для
, ее график будет симметричен относительно начала координат. Поэтому достаточно построить график для  .
.
3. График функции пересекается с осями координат только в начале координат, так как  .
.
4. Исследуем функцию на наличие асимптот:
а) вертикальных асимптот график функции не имеет;
б) невертикальная асимптота имеет уравнение  .
.


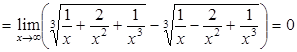 ,
,


 .
.
Таким образом, уравнение асимптоты  .
.
5. Исследуем функцию на экстремум
 .
.
 нигде не обращается в нуль;
нигде не обращается в нуль;  не существует в точках
не существует в точках  , которые являются критическими.
, которые являются критическими.
Исследуем знак производной на интервале [0; ∞)
 |

 0 1
0 1
Рис. 5.
 есть точка максимума,
есть точка максимума,  .
.
6. Исследуем график функции на выпуклость и вогнутость
 .
.
 в точке
в точке  ;
; 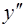 не существует в точках
не существует в точках  . Эти точки могут быть абциссами точек перегиба.
. Эти точки могут быть абциссами точек перегиба.
Исследуем знак второй производной на интервале [0; ∞)









 0 1
0 1
Рис. 6
 не является точкой перегиба.
не является точкой перегиба.
Основываясь на полученных результатах исследования, строим график функции на интервале [0; ∞), затем симметрично полученному графику относительно начала координат на интервале (- ∞; 0)

Рис. 7
Пример 2. Найти наибольшее и наименьшее значения функции
 на отрезке [-4; 4].
на отрезке [-4; 4].
Решение. 1. Найдем критические точки функции  , лежащие внутри отрезка [-4; 4], и вычислим ее значения в этих точках:
, лежащие внутри отрезка [-4; 4], и вычислим ее значения в этих точках:  ;
; 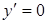 в точках
в точках  и
и  . Эти точки лежат внутри отрезка [-4; 4] и являются критическими. Других критических точек нет, так как производная существует всюду. Значение функции в критических точках:
. Эти точки лежат внутри отрезка [-4; 4] и являются критическими. Других критических точек нет, так как производная существует всюду. Значение функции в критических точках:  и
и  .
.
2. Вычислим значения функции на концах отрезка [-4; 4]:  и
и  .
.
3. Сравнивая все вычисленные значения функции во внутренних критических точках и на концах отрезка, заключаем: наибольшее значение функции  на отрезке [-4; 4] равно 40 и достигается ею во внутренней критической точке
на отрезке [-4; 4] равно 40 и достигается ею во внутренней критической точке  , а ее наименьшее значение равно -41 и достигается на левой границе отрезка
, а ее наименьшее значение равно -41 и достигается на левой границе отрезка  .
.


Во многих геометрических, физических и технических задачах требуется найти наибольшее или наименьшее значение величины, связанной функциональной зависимостью с другой величиной.
Для решения такой задачи следует, исходя из ее условия, выбрать независимую переменную, а затем найти искомое наибольшее или наименьшее значение полученной функции. При этом интервал изменения независимой переменной, который может быть конечным или бесконечным, также определяется из условия задачи.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
ОСНОВНАЯ ЛИТЕРАТУРА
1. Индивидуальные задания по высшей математике. Часть 1. Под общ.ред. А.П.Рябушко. – Минск :Вышэйшая школа,2007. – 367 с.
2. Мацкевич И.П., Свирид Г.П., Булдык Г.М. Сборник задач и упражнений по высшей математике. Мн., Вышэйшая школа. 1996.
Унсович А.Н Высшая математика Учебно-методический комплекс для студентов экономических и инженерно-экономических специальностей. / Барановичский гос. университет. — Барановичи: БарГУ. — 2006. — Ч 1—368с
Унсович А.Н Учебно-методический комплекс для студентов экономических и инженерно-экономических специальностей. / Барановичский гос. университет. — Барановичи: БарГУ. — 2006. — Ч2—192с
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Гусак А.А. Пособие к решению задач по высшей математике. Мн., Издательство БГУ им. Ленина. 1973.
2. Кудрявцев Л.Д. Краткий курс математического анализа. - М.: Наука, 1989.
3. Русак. В. и др. Курс высшей математики: Алгебра и начала анализа. Анализ функции одной переменной. М., Высшая школа. 1994.
4. Справочник по высшей математике / А.А. Гусак, Г.М. Гусак, Е.А. Бричкова. -Минск: ТетраСистемс, 2006. - 640с.
5. ШипачёвВ.С. Высшая математика / Под ред. акад. А.Н.Тихонова. - М.: Высшая школа, 1985. -471с.