Главная | Обратная связь

Колебания в режиме странного аттрактора в реакторе с рециклом

Странные аттракторы

Понятие странного аттрактора

В диссипативных системах при стремлении системы к аттрактору происходит сжатие фазового объёма в точку, если аттрактор - узел или фокус; в замкнутую траекторию, соответствующую устойчивому периодическому движению, если аттрактор - предельный цикл; в тор, соответствующий устойчивому квазипериодическому движению, если аттрактор – двумерный тор. Однако в трёхмерном пространстве состояний существуют ещё и аттракторы непериодические. Это так называемые странные аттракторы - аттракторы, отличные от стационарной точки, предельного цикла и двумерного тора.

В случае странного аттрактора также происходит сжатие фазового объёма диссипативной динамической системы, приводящее к тому, что фазовые траектории с течением времени стягиваются к предельному множеству - странному аттрактору – и, попав в область, занятую им, остаются в ней навсегда. Однако на самом аттракторе движение является неустойчивым. Иначе говоря, поведение системы со странным аттракторомхарактеризуется сочетанием глобального сжатия фазового объёма с локальной неустойчивостью фазовых траекторий.

Фазовые траектории странного аттрактора очень чувствительны к начальным данным. Сочетание сильной зависимости от начальных данных с приближённым их значением обусловливает невозможность точных долговременных прогнозов относительно эволюции систем со странным аттрактором.

С практической точки зрения одной из наиболее чувствительных систем следует считать атмосферу. Лоренц в 1963 г. высказал предположение о том, что динамика атмосферы весьма чувствительна к начальным условиям. Из этой гипотезы вытекают самые серьёзные следствия для предсказания погоды, даже если бы нам удалось усовершенствовать метеорологические модели и сбор данных.

Лоренц обнаружил, что сократив число членов в уравнении Навье-Стокса, можно получить нелинейную систему уравнений с тремя переменными, сохраняющую много характерных особенностей исходной системы. Эту модель мы и рассмотрим более подробно, так как она оказалась наглядным примером трёхмерной системы, обладающей странным аттрактором.

 

Система Лоренца

Исследование типа неподвижных точек

Рассмотрим систему Лоренца:

(13.1)

где - управляющие параметры системы.

Определим неподвижные точки системы Лоренца (13.1) из уравнений:

Видно, что начало координат, т.е. точка O(0, 0, 0), является неподвижной точкой при любых значениях параметров системы. характеристическое уравнение для неё имеет вид:

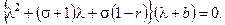
Следовательно, точка О устойчива и является устойчивым узлом, если r < 1.

При r > 1 точка О теряет устойчивость, превращаясь в седло–узел, и в системе возникают ещё две неподвижные точки:

Тип точек O₁ и О₂ определяется с помощью характеристического уравнения:

(13.2)

Точки O₁ и О₂ устойчивы при выполнении условий:

(13.3)

При точки O₁ и О₂ становятся неустойчивыми точками типа седло–фокус. В этом случае характеристическое уравнение (13.2) имеет один действительный отрицательный корень и два комплексно-сопряжённых с положительной действительной частью.

Других неподвижных точек кроме O, O₁ и О₂ система (13.1) не имеет. Поскольку локальный анализ окрестностей неустойчивых неподвижных точек O, O₁ и О₂ не даёт сведений о характере траекторий, для дальнейшего изучения системы Лоренца требуется численное интегрирование уравнений (13.1).

 

Эволюция режимов движения: зарождение метастабильного хаоса

Рассмотрим эволюцию траекторий системы (13.1) при и

При система имеет три неподвижные точки: O, O₁ и О₂. Точка О неустойчива и представляет собой точку типа седло–узел, имеющую двумерную устойчивую область и две выходящие кривые (сепаратрисы) Г₁ и Г₂. Неподвижные точки O₁ и О₂ являются устойчивыми.

При каждая из кривых Г₁ и Г₂ превращается в замкнутую петлю; при этом точки O₁ и О₂ остаются устойчивыми. Фазовый портрет системы Лоренца для этого случая представлен на рисунке (вверху).

При точки O₁ и О₂ по-прежнему являются устойчивыми, а от каждой из замкнутых петель Г₁ и Г₂ рождается по седловой периодической траектории L₁ и L₂. Сепаратрисы Г₁ и Г₂ стремятся теперь соответственно к точкам O₂ и О₁. Кроме того, появляются кривые, идущие от седлового предельного цикла L₁ к L₂ и от L₂ к L₁. Эти кривые образуют множество В₁, но это множество не является притягивающим и, следовательно, аттрактором. седловые периодические траектории L₁ и L₂ являются границами областей притяжения стационарных точек O₁ и О₂. Фазовая кривая, начавшаяся вне этих областей, может совершать колебания из окрестности L₁ в окрестность L₂ и обратно, пока не попадёт в область притяжения одного из аттракторов - О₁ или O₂, причём по мере приближения параметра r к значению число колебаний существенно возрастает. Такое поведение системы называют метастабильным хаосом. Проекция основных элементов фазового портрета системы Лоренца для этого случая на координатную плоскость (x, z) показана на рисунке (внизу).

 

Эволюция режимов движения: появление аттрактора Лоренца

Рассмотрим эволюцию траекторий системы (13.1) при и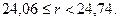

При стационарные точки O₁ и О₂ согласно (13.3) ещё являются устойчивыми, но сепаратрисы Г₁ и Г₂ уже не стремятся к ним, а наматываются на седловые траектории L₂ и L₁, соответственно (см. рисунок). Теперь на месте множества В₁ возникает множество В₂, которое при становится устойчивым и притягивающим.

При точки O₁ и О₂ по-прежнему устойчивы. Однако кроме них в фазовом пространстве системы имеется предельное множество В₂, называемое аттрактором Лоренца. Множество В₂ представляет собой совокупность кривых, идущих от L₁ к L₂ и обратно; кроме них В₂ содержит седловую точку О и её сепаратриссы Г₁ и Г₂.

Таким образом, при в системе Лоренца имеются два типа аттракторов: стационарные точки O₁ и О₂ и аттрактор Лоренца В₂. Область притяжения В₂ ограничена устойчивым многообразием седловых предельных циклов L₁ и L₂ (см. рисунок). Фазовые траектории системы в зависимости от начальных условий с течением времени стремятся либо к точке O₁, либо к точке О₂, либо совершают колебания, случайным образом переходя от вращения вокруг точки O₁ к вращению вокруг точки O₂ и обратно. Следовательно, в зависимости от начальных условий в системе (13.1) могут реализоваться существенно различные режимы движения: стационарный или хаотический.

 

Фазовый портрет аттрактора Лоренца

Рассмотрим поведение системы (13.1) при и

При седловые предельные циклы L₁ и L₂ стягиваются соответственно к стационарным точкам O₁ и О₂ и при исчезают, сливаясь с ними; согласно (13.3), стационарные точки O₁ и О₂ становятся при этом неустойчивыми.

При все стационарные точки (О, O₁ и О₂) являются неустойчивыми. Единственным устойчивым предельным множеством - аттрактором - будет В₂, т. е. аттрактор Лоренца (см. рисунок). Следовательно, в системе (13.1) при любых начальных условиях будет устанавливаться хаотический режим движения. Хаотическая траектория аттрактора, представленного на рисунке (внизу), просчитывалась при и начальных условиях плоскость (x, y) соответствует z = 27.

Таким образом, можно сделать вывод, что диссипативные динамические системы (например, система Лоренца), размерность фазового пространства которых больше или равна трём, могут иметь наряду с регулярными и очень сложные, хаотические режимы движения. Математическим представлением такого хаотического поведения диссипативных систем является притягивающее множество сложной структуры - странный аттрактор.

 

Колебания в режиме странного аттрактора в реакторе с рециклом