Главная | Обратная связь

Составить систему узловых уравнений, определить потенциалы, напряжения на ветвях и токи в ветвях.

 

Метод узловых потенциалов (напряжений)

Сущность этого метода сводится к решению системы уравнений, составленных только по первому закону Кирхгофа. Из этих уравнений определяют напряжение в узлах схемы электрической цепи относительно некоторого базисного узла, потенциал которого изначально принимают равным нулю.

Такое допущение не изменяет условий задачи, так как ток в каждой ветви зависит не от абсолютных значений потенциалов узлов, к которым присоединена ветвь, а от разности потенциалов между концами ветви.

А токи в ветвях, соединяющих узлы, находят по закону Ома.

Обратимся к полученной нами электрической схеме рис. 32 с четырьмя узлами (1), (2), (3), (4).

 

 

Рис. 32

J4

E1

E6

I6

R6

I4

(1)

(2)

(4)

J5

I5

I2

R5

I3

(3)

E3

R3

I1

R2

IR5

 

.

Проведем анализ схемы

Электрическая схема имеет 6 (шесть) ветвей В и шесть неизвестных токов. Число узлов У в схеме 4 (четыре), следовательно, по первому закону Кирхгофа необходимо составить три уравнения, и по второму тоже три.

Решение задачи методом контурных токов потребовало бы составления трех уравнений. В нашем случае применяя метод узловых потенциалов, необходимо составить

y-1=4-1=3 уравнений.

В качестве базисного узла (узла, потенциал которого считаем равным нулю) можно выбрать любой узел.

Однако, если какая-нибудь ветвь содержит идеальный источник ЭДС и, следовательно, напряжение между двумя узлами задано, целесообразно в качестве базисного узла выбрать один из узлов данной ветви. В этом случае число неизвестных узловых напряжений и, стало быть, число узловых уравнений уменьшается на единицу.

Так как первая ветвь содержит идеальный источник ЭДС, в качестве базисного узла (заземленного узла) возьмем узел, обозначенный на рис. 32 цифрой (1). В этом случае потенциал первого узла 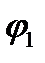равен нулю ( 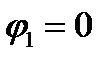). Остаются неизвестными три узловых потенциала .

В общем случае для электрической схемы с четырьмя узлами имеем следующую систему уравнений, составленных по методу узловых потенциалов:

(66)

Однако, в связи с тем, что 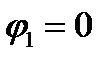и, следовательно, члены , имеем из уравнений (66):

(67)

где:

- суммы проводимостей ветвей, присоединенных соответственно к узлам (2), (3), (4). Они называются собственными проводимостями узлов (2), (3), (4);

- суммы проводимостей ветвей между соответствующими узлами (соединяющих эти узлы), называемые общими проводимостями между соответствующими узлами.

В правой части каждого из уравнений стоят алгебраические суммы произведений из ЭДС на проводимости ветвей, примыкающих к узлу, для которого составлено уравнение (ЭДС в ветвях заменяем источником тока J. Причем это можно сделать не изменяя схему цепи: оставить в ветви с источником ЭДС все сопротивления и учесть, что между узлами этой ветви подсоединен источник тока, у которого величина тока равна произведению ЭДС на суммарную проводимость ветви ).

Причем ЭДС, направленная к узлу, берется с положительном знаком, а направленная от узла – с отрицательным.

Точно также поступаем и с источниками тока J. Если ток источника направлен к узлу, берем его в правую часть уравнения со знаком плюс. Если ток источника тока направлен от узла, то его в правую часть уравнения берут со знаком минус.

Уравнения (67) не зависят от выбранных положительных направлений токов в ветвях.

Так как в первой ветви находится идеальный источник ЭДС, то , однако 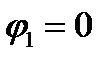, следовательно

. (68)

Таким образом остаются неизвестными лишь два потенциала и . В этой связи, в системе уравнений (67), уравнение для четвертого узла лишнее (избыточное), так как для определения двух неизвестных, необходимо иметь два уравнения. Следовательно, система уравнений (67) преобразуется к виду:

. (69)

Теперь для решения системы уравнений (69) необходимо определить проводимости ветвей: :

; ;

 

; .

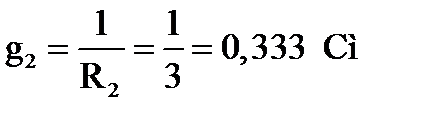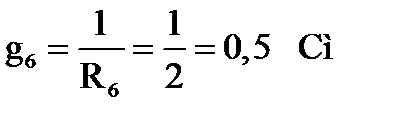Далее определяем собственные проводимости 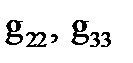и общие проводимости .

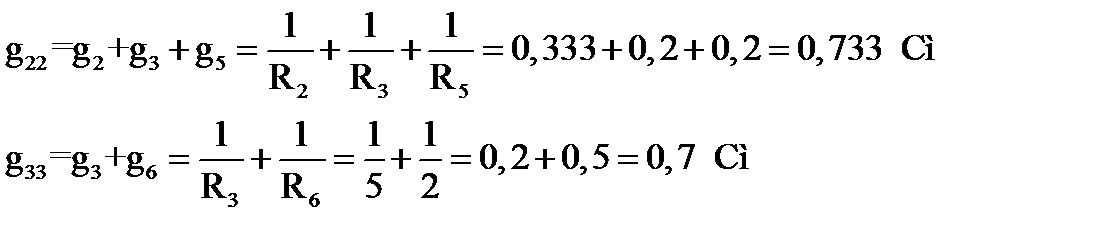
(70)

.

 

Теперь рассчитываем правые части системы уравнений (69):

(71)

Подставим в (69) численные значения найденных коэффициентов и потенциала , получим:

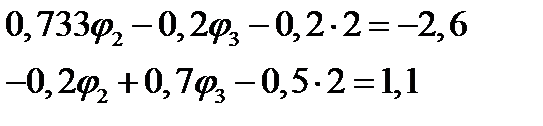, далее

И теперь окончательно получаем систему уравнений для определения потенциалов и :

.

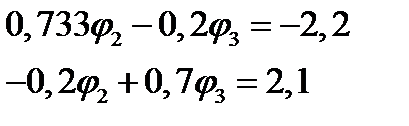Решим эту систему уравнений при помощи определителей:

(73)

. (74)

Таким образом:

(75)

 

.

Далее определяем токи:

.

 

Проверим правильность расчета, используя уравнения пункта (5) и (8):

(77)

 

Таким образом, в пределах погрешности расчета, полученные результаты совпадают с ранее полученными, что говорит о верности расчета.