 |
|
Определить токи в ветвях
Метод контурных токов сводится к составлению и решению систем уравнений, получаемых только по второму закону Кирхгофа применительно к понятиям контурных токов, сопротивлений и ЭДС.
Вводя понятие о контурных токах, можно свести уравнения, составленные по законам Кирхгофа, к системе уравнений, составленных для независимых контуров, т.е. исключить уравнения, составляемые по первому закону Кирхгофа. Благодаря этому удается снизить порядок системы уравнений.
| Рис. 33 |
| E1 |
| I3 |
| R3 |
| I5 |
| R5 |
| E3 |
| III |
| E2 |
| R2 |
| R1 |
| I2 |
| R4 |
| I33 |
| I22 |
| II |
| I |
| I11 |
| I4 |
| I1 |
Будем считать, что в каждом контуре имеется свой контурный ток I11, I22, I33. направление контурных токов выбираем одинаково – по часовой стрелке. Однако в общем случае, и особенно при решении четырехполюсников, направление обхода контура выбирается так, как это удобно, т.е. произвольно. Сопоставляя контурные токи с токами ветвей, можно показать, что значения контурных токов совпадают со значениями действительных токов только во внешних ветвях:
 .
.
Токи смежных ветвей равны разности контурных токов соседних контуров:
 .
.
Таким образом, по известным контурным токам легко можно найти действительные токи всех ветвей.
Для определения контурных токов I11, I22, I33, рис. 33, необходимо составить для трех контуров уравнения по второму закону Кирхгофа.
Для этой цели определяем собственные сопротивления контуров R11, R22, R33, которые равны сумме сопротивлений всех элементов, входящих в контур:

(считаем, что  равны нулю – источники ЭДС – идеальные (внутренние сопротивления равны нулю)).
равны нулю – источники ЭДС – идеальные (внутренние сопротивления равны нулю)).
Далее определяем взаимные (общие) сопротивления смежных контуров  , представляющие собой сопротивления, входящие одновременно в каждый из двух смежных контуров (сопротивление общей ветви 2-х контуров), таким образом:
, представляющие собой сопротивления, входящие одновременно в каждый из двух смежных контуров (сопротивление общей ветви 2-х контуров), таким образом:
 (сопротивление R2 одновременно принадлежит первому I и II контурам); сопротивление связи первого контура со вторым;
(сопротивление R2 одновременно принадлежит первому I и II контурам); сопротивление связи первого контура со вторым;
 (сопротивление R5 одновременно принадлежит второму II и III контурам); сопротивление связи второго контура с третьим.
(сопротивление R5 одновременно принадлежит второму II и III контурам); сопротивление связи второго контура с третьим.
Теперь составляем уравнения по второму закону Кирхгофа для каждого из контуров I, II, III:
При составлении уравнений по второму закону Кирхгофа для контура необходимо учитывать, что алгебраическая сумма падений напряжений выражается произведением тока рассматриваемого контура Inn на его собственное сопротивление Rnn, взятое со знаком «плюс», и произведением тока другого (смежного) контура Inn на общее сопротивление контуров Rnm, (где n – 1, 2, 3…; m – 2, 3…) взятое со знаком «минус». Итак, имеем следующие уравнения:
Для I контура: 
Для II контура:  (78)
(78)
Для III контура:  .
.
Или в общем виде:
 (79)
(79)
Решая эту систему уравнений, можно найти контурные токи, а по ним искомые токи ветвей:  .
.
Уравнения для контурных токов можно записать в матричной форме:
 (80)
(80)
Здесь [R] – квадратная матрица коэффициентов при неизвестных токах контуров;
[I] – матрица столбец неизвестных контурных токов;
[Е] – матрица столбец известных контурных ЭДС:
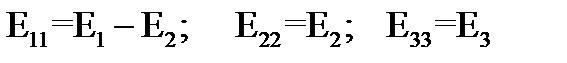 .
.
Если какие-либо контуры не имеют общих ветвей, то соответствующие элементы матрицы равны нулю.
Так для нашей цепи рис. 33, имеем:
 (81)
(81)
Решением уравнения (80) будет
 , где (82)
, где (82)
 - матрица, обратная матрице коэффициентов
- матрица, обратная матрице коэффициентов  .
.
Применим вышеизложенную методику для решения нашей задачи (схемы замещения). Решение проведем, используя метод контурных токов.
| Рис. 34 |
| J4 |
| E1 |
| E6 |
| I6 |
| R6 |
| I4 |
| J5 |
| I5 |
| I2 |
| R5 |
| I3 |
| E3 |
| R3 |
| I1 |
| R2 |
| I |
| I11 |
| I22 |
| II |
| J4 |
| J4 |
| J5 |
| IR5 |
На рисунке 34 выбраны независимые контуры I, II и их направления обхода (положительные направления контурных токов I11, II22, по часовой стрелке).
Число уравнений по второму закону Кирхгофа равно количеству независимых контуров (контуры, отличающиеся хотя бы одной ветвью).
Для нашей схемы число независимых контуров равно N=2, ветвь с источником тока не может создать независимый контур. Значит и уравнений по второму закону Кирхгофа будет два (N=2).
Контурные токи I11, II22 совпадают со значениями действительных токов только во внешних ветвях:

 (83)
(83)
Токи смежной ветви  равны разности контурных токов соседних контуров:
равны разности контурных токов соседних контуров:
 . (84)
. (84)
Далее определяем собственные сопротивления контуров (сопротивлений, входящих в замкнутый контур)
 . (85)
. (85)
и взаимные (общие) сопротивления смежных контуров I и II, представляющие собой сопротивления, входящие одновременно в каждый из двух смежных контуров (сопротивление общей ветви 5 (R5) контуров I и II), таким образом:
 . (86)
. (86)
Теперь составим уравнения по второму закону Кирхгофа для каждого из контуров I и II. При составлении уравнений по второму закону Кирхгофа для контура, необходимо учитывать, что алгебраическая сумма падений напряжений выражается произведением тока рассматриваемого контура (для I контура –I11) на его собственное сопротивление R11 [для второго конура –I22 R22], берется со знаком плюс «+», а произведение тока другого контура (смежного) II. I22 на общее сопротивление контуров  , берется со знаком минус «-». Уравнения имеют вид:
, берется со знаком минус «-». Уравнения имеют вид:

 , (87)
, (87)
или

 . (88)
. (88)
Эти уравнения записаны с учетом того, что J5 как контурный ток «замыкаем» через сопротивление R5, а J4, как контурный ток «замыкаем» через 
В матричной форме уравнения принимают вид:
 (89)
(89)
Подставив значения всех параметров в матричное уравнение (89), получим:
 (90)
(90)
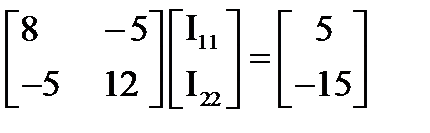 . (91)
. (91)
Используя сведения по решению уравнений с квадратными матрицами (при помощи определителей), имеем
 (92)
(92)
 . (93)
. (93)
Рассчитываем токи в ветвях:
 (94)
(94)
 .
.
Результат получили тот же, что и при расчете цепи методом узловых потенциалов.
Применим вышеизложенную методику для нашей схемы замещения, но положительные направления контурных токов выберем против часовой стрелки.
| Рис. 35 |
| J4 |
| E1 |
| E6 |
| I6 |
| R6 |
| I4 |
| J5 |
| I5 |
| I2 |
| R5 |
| I3 |
| E3 |
| R3 |
| I1 |
| R2 |
| I |
| I11 |
| I22 |
| II |
| J4 |
| (4) |
| (3) |
| (2) |
| (1) |
| IR5 |
На рисунке (рис. 35) выбраны независимые контуры I, II и их направления обхода (положительные направления контурных токов I11, I22 против часовой стрелки).
Число уравнений равно числу независимых контуров, ветвь с источником тока не может создать независимый контур (контур, отличающийся от других контуров хотя бы одной ветвью).
Для нашей схемы число независимых контуров N=2. значит и уравнений по второму закону Кирхгофа 2 (два).
Контурные токи I11, I22 совпадают со значениями действительных токов только во внешних ветвях:
 . (95)
. (95)
Токи смежной ветви  равны разности контурных токов соседних контуров
равны разности контурных токов соседних контуров
 . (96)
. (96)
Далее определяем собственные сопротивления контуров  (97)
(97)
и взаимные (общие) сопротивлении смежных контуров I и II, представляющие собой сопротивления, входящие одновременно в каждый из двух смежных контуров (сопротивление общей ветви 5 контуров I и II). Таким образом:
 . (98)
. (98)
Теперь составляем уравнения по второму закону Кирхгофа для каждого из контуров I, II:
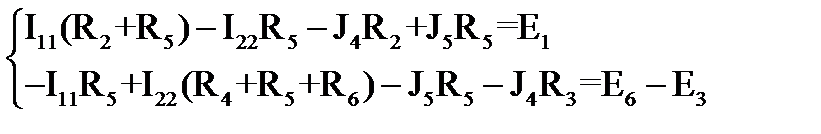 . (99)
. (99)
Эти уравнения записаны с учетом того, что J5 как контурный ток «замыкаем» через R5, а J4 как контурный ток «замыкаем» через 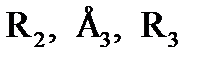 . В матричной форме уравнения принимают вид:
. В матричной форме уравнения принимают вид:
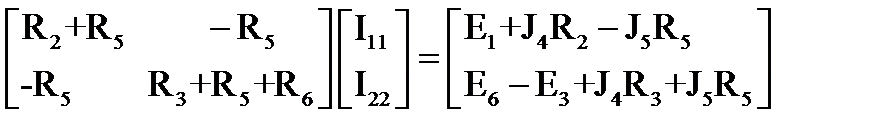 . (100)
. (100)
Подставив значения всех параметров в матричное уравнение (100), получим:
 , (101)
, (101)
 . (102)
. (102)
Используя теорию по решению уравнений при помощи определителей, имеем
 (103)
(103)
 (104)
(104)
 . Следовательно:
. Следовательно:
 (105)
(105)
 .
.
Данный результат сравниваем с результатом, полученным при решении методом узловых потенциалов и методом уравнений Кирхгофа.
 (106)
(106)
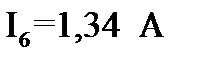 .
.
Как видно из сравнения результаты совпадают с точностью ошибки вычислений. А это вполне удовлетворительно.
12. Определить ток I3 в третьей ветви методом эквивалентного генератора
Важным принципом эквивалентности, широко применяемым при анализе линейных электрических цепей, является принцип эквивалентного генератора (теорема об активном двухполюснике или теорема Гельмгольца – Тевенена).
Он формулируется следующим образом:
любая линейная электрическая цепь, рассматриваемая относительно двух выводов (активный двухполюсник), эквивалентна реальному источнику с ЭДС, равной напряжению между этими выводами при размыкании внешнего участка цепи, подключенного к этим выводам (режим холостого хода), и внутренним сопротивлением, равным входному сопротивлению пассивного двухполюсника, получающегося при равенстве нулю всех ЭДС для источников ЭДС и токов для источников тока рассматриваемого двухполюсника.
| А |
| Рис. 36 |
| R3 |
| E3 |
| (3) |
| (2) |
| Рис. 37 |
| R3 |
| E3 |
| (3) |
| (2) |
| I3 |
| Eэг |
| Rвнэг |
Теперь легко найти ток I3 в простой электрической цепи:
 . (107)
. (107)
Чтобы определить ток I3, необходимо определить параметры эквивалентного генератора 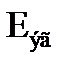 и
и  .
.
Таким образом, главное содержание расчета цепи методом эквивалентного генератора состоит в определении эквивалентных параметров 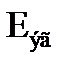 и
и  - внутренней части цепи.
- внутренней части цепи.
| Рис. 38 |
| E1 |
| I6 |
| IR5 |
| J4 |
| (1) |
| U23хх |
| I1 |
| E6 |
| R6 |
| (4) |
| J5 |
| I5 |
| I2 |
| R5 |
| (2) |
| R2 |
| (3) |
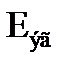 равна напряжению на выводах внутренней цепи
равна напряжению на выводах внутренней цепи 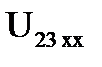 (режим холостого хода), при отключенной внешней части (ветви
(режим холостого хода), при отключенной внешней части (ветви  ,
,  ) (рис. 38).
) (рис. 38).
Принимаем  . (108)
. (108)
Учитывая, что 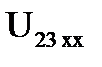 имеет положительное направление от узла (2) к узлу (3), т.е.
имеет положительное направление от узла (2) к узлу (3), т.е.
 . (109)
. (109)
| (2) |
| (3) |
| Eэг |
| Rвмэг |
| Рис. 39 |
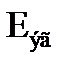 и сопротивлением
и сопротивлением  .
.
Учитывая (109), можно записать, что
 . (110)
. (110)
Таким образом для определения 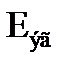 необходимо найти потенциалы
необходимо найти потенциалы  . Потенциал
. Потенциал 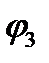 найдем с учетом того, что в ветви, состоящей из Е6, R6, протекает ток J4, как ток идеального источника тока.
найдем с учетом того, что в ветви, состоящей из Е6, R6, протекает ток J4, как ток идеального источника тока.
Следовательно
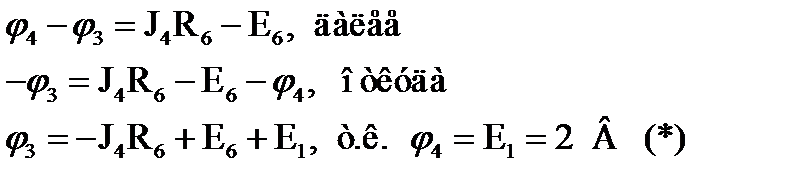
Подставляя значение  в формулу (*), получим:
в формулу (*), получим:
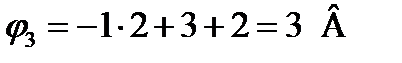 . (111)
. (111)
Теперь определим потенциал т. (2), по второму закону Кирхгофа, воспользовавшись тем, что для контура (1), (2), (4), (1), можно определить ток I2, который один и тот же в ветви (1) – (4), т.е.  . Потенциал
. Потенциал  определяем из уравнения
определяем из уравнения  . Откуда, с учетом
. Откуда, с учетом 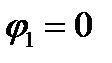 , имеем
, имеем  , откуда
, откуда  . Уравнение для указанного контура, согласно второму закону Кирхгофа, имеет вид:
. Уравнение для указанного контура, согласно второму закону Кирхгофа, имеет вид:  .
.
Откуда  , следовательно
, следовательно
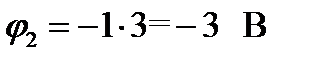 . (112)
. (112)
Найдем напряжение 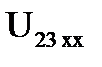 :
:

 . (113)
. (113)
Определим потенциал второго узла  методом узловых потенциалов. Для этого определяем собственную и общую проводимость.
методом узловых потенциалов. Для этого определяем собственную и общую проводимость.
Собственная проводимость узла (2) равна сумме всех проводимостей ветвей, примыкающих к этому узлу. К узлу (2) примыкает ветвь 2 с проводимостью  и ветвь 5 с проводимостью
и ветвь 5 с проводимостью  .
.
Таким образом, собственная проводимость узла (2) в уравнениях записывается со знаком плюс «+» и равна:
 . (114)
. (114)
Теперь определяем общую проводимость между узлами (2) и (4). Узел (2) связан с узлом (4) общей проводимостью
 . (115)
. (115)
Общая проводимость в уравнения цепи вносится со знаком минус «-» -  .
.
Чтобы составить узловые уравнения для потенциала любого узла электрической цепи, необходимо определить собственную проводимость узла (сумма всех проводимостей ветвей, примыкающих к узлу цепи), общую проводимость (проводимость между двумя узлами). Собственные проводимости узлов  записываются со знаком плюс, а общие проводимости
записываются со знаком плюс, а общие проводимости  записываются со знаком минус. Если ЭДС направлены к узлу, берутся со знаком плюс, в противном случае со знаком минус. Также, ток источника тока берется в уравнении со знаком плюс, если он направлен к узлу и с минусом – если он направлен от узла.
записываются со знаком минус. Если ЭДС направлены к узлу, берутся со знаком плюс, в противном случае со знаком минус. Также, ток источника тока берется в уравнении со знаком плюс, если он направлен к узлу и с минусом – если он направлен от узла.
Для составления уравнения узлового потенциала необходимо в левой части уравнения взять произведение потенциала узла на собственную проводимость  со знаком плюс, произведение потенциала узла
со знаком плюс, произведение потенциала узла  , который связан с заданным, на общую проводимость между этими узлами
, который связан с заданным, на общую проводимость между этими узлами  со знаком минус. Итак, левая часть узлового уравнения для узла (2) относительно узла (4) будет иметь вид:
со знаком минус. Итак, левая часть узлового уравнения для узла (2) относительно узла (4) будет иметь вид:  . (116)
. (116)
В правой части берется сумма произведений ЭДС на проводимости ветвей и токов источников тока, при чем, если ЭДС и ток источника тока направлено к узлу, то эти слагаемые берутся со знаком плюс, в противном случае – со знаком минус.
Уравнение правой части для узлового потенциала узла (2) по отношению к узлу (4) будет иметь следующий вид, так как J5 направлен от узла (2) и ЭДС отсутствуют, равно
 . (117)
. (117)
Полное уравнение для узла (2) относительно узла (4) будет иметь следующий вид:
 . (118)
. (118)
Потенциал узла (4) известен из предыдущего решения:

Далее подставляем значения  в уравнение (118):
в уравнение (118):  , откуда
, откуда  , следовательно,
, следовательно,
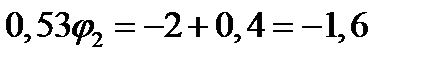 и, окончательно,
и, окончательно,
 . (119)
. (119)
Результат этого метода чуть завышен, это определяется точностью, с которой мы определяем проводимости ветвей. В нашем случае мы взяли точность определения проводимостей до второго знака после запятой  . Если вычислять с точностью до 3, 4, 5 знаков, то результат будет точнее.
. Если вычислять с точностью до 3, 4, 5 знаков, то результат будет точнее.
Таким образом, точность метода узловых потенциалов зависит от точности определения проводимостей ветвей, чем с большей точностью (до 3-го, 4-го, 5-го значащего числа после запятой) мы определяем проводимости ветвей, тем точнее метод узловых потенциалов.
Определяем внутреннее сопротивление эквивалентного генератора  , которое равно общему сопротивлению внутренней части цепи
, которое равно общему сопротивлению внутренней части цепи 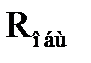 относительно узлов (2) и (3) при равенстве нулю всех ЭДС для источников ЭДС и токов для источников тока для рассматриваемого двухполюсника и отключенной внешней части цепи (
относительно узлов (2) и (3) при равенстве нулю всех ЭДС для источников ЭДС и токов для источников тока для рассматриваемого двухполюсника и отключенной внешней части цепи (  ).
).
| Рис. 40 |
| (2) |
| (3) |
| R5 |
| R2 |
| R6 |
 , приобретает вид:
, приобретает вид:
Которая получена из схемы (рис. 38).
| Рис. 41 |
| (2) |
| (3) |
| R5 |
| R2 |
| R6 |
Анализируя схемы рис. 40, рис. 41, приходим к выводу, что R2 и R5 включены параллельно и к ним последовательно подключено сопротивление R6. Общее сопротивление относительно узлов (2) и (3) будет равно сумме общего сопротивления параллельно включенных резисторов R2 и R5 и сопротивления R6, следовательно  .
.
Подставляем значение  и
и  в уравнение для
в уравнение для  , получаем:
, получаем:

Таким образом, выходное сопротивление двухполюсника, равное внутреннему сопротивлению  равно
равно  .
.
Теперь можно определить ток в третьей ветви  .
.
Результат совпадает со всеми результатами расчета тока I3 другими методами.
13. Проверяем соблюдение баланса мощности в электрической цепи. Определяем расход энергии за t = 10 с.
Баланс мощностей
Из закона сохранения энергии следует, что сумма мощностей, развиваемых источниками электрической энергии, равна сумме мощностей потребителей  .
.
Причем для источника ЭДС, направления ЭДС которого совпадает с направлением тока, то источник ЭДС доставляет в цепь энергию в единицу времени (мощность), равную  , и произведение EI входит в уравнение энергетического баланса с положительным знаком.
, и произведение EI входит в уравнение энергетического баланса с положительным знаком.
Если направление ЭДС и тока противоположны, то источник ЭДС не поставляет мощность в цепь (рис. 43), а потребляет ее  , и произведение EI войдет в управление энергетического баланса с отрицательным знаком.
, и произведение EI войдет в управление энергетического баланса с отрицательным знаком.
| Рис. 42 |
| Uab |
| b |
| a |
| Eэг |
| + |
| - |
| I |
| +EI |
| + |
| - |
| Рис. 44 |
| Uab |
| b |
| a |
| y |
| I |
| +UabJ |
| Рис. 43 |
| Uab |
| b |
| a |
| Eэг |
| + |
| - |
| I |
| -EI |
| + |
| - |
| Рис. 45 |
| -Uab |
| b |
| a |
| y |
| I |
| -UabJ |
Для источника тока, если направление тока внутри источника J и напряжение между его выводами Uab противоположны (рис. 44).
 .
.
Если же направление тока внутри источника J и напряжения между его выводами Uab совпадают по направлению, то (рис. 45):
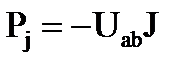 .
.
Составим баланс мощностей цепи согласно выражению


1. Для первой ветви, в которой имеется идеальный источник ЭДС и направление ЭДС Е1 совпадает с током I1, следовательно:
 .
.
2. Во второй ветви источников электрической энергии нет. Ветвь потребляет электрическую энергию:
 .
.
3. В третьей ветви имеется источник ЭДС Е3 и сопротивление R3. Так как направление тока I3 встречно направлению ЭДС Е3, то источник ЭДС не поставляет энергию, а потребляет ее и произведение E3 I3 войдет в уравнение энергетического баланса с отрицательным знаком:
 .
.
Сопротивление R3 является приемником электрической энергии. Мощность, выделяемая на нем равна:
 .
.
4. В четвертой ветви имеется идеальный источник тока, причем направление тока J4 и напряжение  по направлению совпадают, следовательно
по направлению совпадают, следовательно
 .
.
5. В пятой ветви также имеется источник тока J5, направление тока внутри источника тока J5 и направление напряжения  не совпадают, значит:
не совпадают, значит:
 .
.
Сопротивление R5 в этой же цепи является приемником электрической энергии, следовательно,
 .
.
6. В шестой ветви имеется источник ЭДС Е6 и сопротивление R6. Источник ЭДС является источником электрической энергии. Направление ЭДС Е6 и направление тока I6 совпадают, следовательно:
 .
.
Сопротивление R6 является приемником электрической энергии. Мощность, потребляемая в нем равна  .
.
Проанализировав, каким образом электрическая энергия источников электрической энергии перераспределяется в ветвях электрической цепи составим в соответствии с выражением  ;
;  уравнение баланса мощностей:
уравнение баланса мощностей:

Подставляем в уравнение баланса мощностей значения всех величин, полученных при решении электрической цепи:
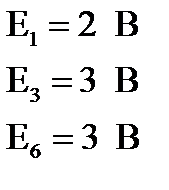
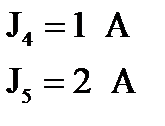
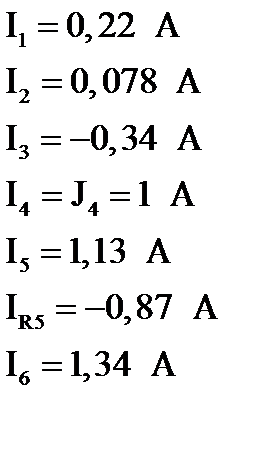

получим:

 . Далее
. Далее

 и окончательно:
и окончательно:

Таким образом, мы убедились, что при верном решении баланс мощностей цепи выполняется.
В этой связи делаем вывод, что наиболее полной (исчерпывающей) проверкой правильности расчета электрической цепи является выполнения условия баланса мощностей. Поэтому полезно составлять баланс мощностей даже в тех случаях, когда по условию задачи его можно и не составлять.
Определяем расход энергии за 10с.: если для поддержания тока I в каком-либо участке электрической цепи требуется иметь на зажимах участка напряжение U, то работа электрического тока на этом участке за время t может быть выражена формулой 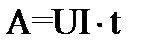 , а соответствующая мощность
, а соответствующая мощность 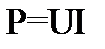 .
.
Если напряжение в этих формулах выражено в вольтах, ток – к амперах, а время – в секундах, то мощность измеряется в ваттах (Вт), а работа в джоулях (Дж) или ватт - секундах (1 ватт - секунда = 1 вольт – ампер – секунда = 1 джоуль).
Если же время выражать не в секундах, а в часах (ч), то работа получается в более крупных единицах – ватт – часах (Вт ч). Значит 1 Вт ч = 3600 Дж.
Энергия, расходуемая за t = 10 с в электрической цепи при мощности источников 9,78 Вт равна:
