Главная | Обратная связь

Краткие теоретические сведения

Электромагнитные поля, независящие от времени ( ), но связанные с движущимися зарядами , называются стационарными. При этом из уравнения непрерывности (1) следует, что

, (2.1)

т.е. линии тока проводимости должны быть замкнутыми, что в свою очередь приводит к отсутствию объемных зарядов в трубках тока (отметим, что естественной трубкой тока является проводник с током). Действительно, условие (2.1) означает, что поток плотности тока через замкнутую поверхность равен нулю; рассматривая в качестве замкнутой поверхности векторную трубку линий плотности тока (см. рис.2.1), получаем:

. (2.2)

Следовательно, J = const, т.е. стационарные поля связаны с постоянным током.Т.к.при этомзаряд, протекающий в единицу времени через сечение S₁, равен заряду, вытекающему через сечение S₂, то в объеме рассматриваемой векторной трубки объемный заряд отсутствует.

С учетом сказанного уравнения Максвелла, описывающие стационарные поля, принимают вид:

1) , 3) ,

2) , 4) 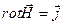. (2.3)

Из уравнения 1) и 2) системы (2.3) следует, что электрическая составляющая стационарного поля - безвихревая ( ), но не связана с зарядами. Другими словами, эти уравнения лишь описывают электрическое поле, но не объясняют причин возникновения и существования постоянного тока. Для существования постоянного тока кроме потенциального электрического поля необходимо наличие и поля сторонних сил неэлектростатического происхождения. При этом уравнения (2.3) дополняются законом Ома, в общем случае имеющем вид:

, (2.4)

где электропроводность g является величиной, обратной удельному сопротивлению среды. Циркуляция по замкнутому контуру называется электродвижущей силойисточника тока (ЭДС):

. (2.5)

Потенциальная составляющая электрического поля описывается теми же уравнениями, что электростатическое поле, поэтому в дальнейшем рассматриваться не будет.

Т.к. магнитная составляющая стационарного поля от времени не зависит, то часть электродинамики, изучающая магнитное поле постоянного тока, называется магнитостатикой. Уравнения 3) и 4) системы (2.3) являются уравнениями магнитостатики. Эти уравнения могут быть записаны в виде одного основного уравнения магнитостатики, если ввести векторный потенциал . Действительно, из уравнения 3) системы (2.3) следует, что индукцию магнитного поля можно представить как

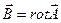, (2.6)

причем векторный потенциал определен с точностью до градиента произвольной скалярной функции. Подставляя (2.6) в уравнение 4) системы (2.3), получаем основное уравнение магнитостатики в виде уравнения Пуассона для векторного потенциала:

. (2.7)

Очевидно, что в области пространства, где токи отсутствуют, уравнение Пуассона переходит в уравнение Лапласа для векторного потенциала. Так же, как и скалярный потенциал, векторный потенциал должен быть непрерывен на границе раздела сред, а поведение его производных определяется граничными условиями (7) для векторов и .

Основной задачей магнитостатики является нахождение поля заданного распределения токов и сил, действующих на токи, помещенные в рассматриваемую область магнитного поля. Такая задача в общем случае сводится к решению уравнения (2.7) с последующим определением вектора индукции в соответствии с (2.6).

Так же, как и в электростатике, во многих случаях решение основной задачи магнитостатики может быть более простым при использовании принципа суперпозиции для индукции магнитного поля или для векторного потенциала. Так, поле элемента тока определяется следующими выражениями:

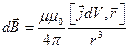, , (2.8)

если начало координат совмещено с элементом тока, или

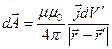, , (2.9)

если 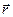- радиус-вектор точки наблюдения поля, - радиус-вектор элемента тока и (см. рис.2.2). Интегрирование (2.9) по объему, занятому токами, приводит к

, (2.10)

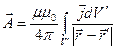. (2.11)

Для линейного тока (тонкого проводника с током) выражения (2.10) и (2.11) принимают вид:

(2.12)

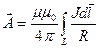, (2.13)

где R – расстояние от элемента тока 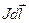до точки наблюдения поля.

Индукция магнитного поля движущегося со скоростью v точечного заряда q в точке С, радиус-вектор которой относительно заряда равен 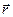, определяется выражением:

. (2.14)

На элемент объемно распределенных токов и на элемент линейного тока во внешнем магнитном поле с индукцией действует сила Ампера, соответственно равная

(2.15)

и . (2.16)

На точечный заряд q, движущийся со скоростью v в магнитном поле с индукцией , действует сила Лоренца

. (2.17)

На большом расстоянии от системы токов в нулевом приближении векторный потенциал равен нулю, а в первом приближении

, (2.18)

где - магнитный момент, равный

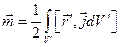. (2.19)

Для витка с током 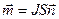, (2.20)

где S - площадь витка, а - нормаль к этой площади (с конца вектора ток обтекает поверхность витка против часовой стрелки).

Индукция поля магнитного момента определяется выражением, аналогичным (1.23) в электростатике:

. (2.21)

При расчете индукции магнитного поля той или иной конфигурации токов широко используются формулы (2.10) – (2.13) и (2.21). В случае осевой симметрии магнитного поля линейного тока и существования контуров, вдоль которых величина поля остается неизменной, наиболее простым методом расчета является использование закона полного тока

. (2.22)

Поскольку все вещества состоят из атомов и молекул, которые можно рассматривать как связанные токи, то любая среда является магнетиком. Для характеристики степени отклика вещества на воздействие магнитного поля вводится понятие вектора намагничения как магнитного момента единицы объема магнетика. На границе раздела двух магнетиков граничные условия (7) дополняются условием

, (2.23)

где i¢ - поверхностная плотность связанных токов.

В слабых полях в однородном и изотропном магнетике вектор намагничения пропорционален напряженности магнитного поля:

, (2.24)

где c - магнитная восприимчивость. Связь между векторами и осуществляется соотношением:

. (2.25)

Тогда . (2.26)

Магнитная восприимчивость c может быть как положительной, так и отрицательной. Вещества с c < 0 (m < 1) являются диамагнетиками; вещества с c > 0 (m > 1) - парамагнетиками и вещества с c >> 1 – ферромагнетиками.

Энергия магнитного поля в объеме V определяется выражением:

. (2.27)

Если система токов занимает конечный объем V¢, то (2.27) можно преобразовать к виду:

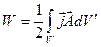. (2.28)

Для контура с линейным током (2.28) переходит в . Тогда энергию системы линейных токов можно рассчитать по формуле:

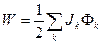, (2.29)

где Ф_k – магнитный поток, пронизывающий k-тый контур с током и создаваемый всеми токами системы. Если ввести коэффициенты индукции L_ik такие, что

(2.30)

(L_ii – коэффициенты самоиндукции, L_ik = L_ki – коэффициенты взаимной индукции), то полная энергия системы замкнутых линейных токов равна

, (2.31)

а энергия одного проводника с током

. (2.32)

Энергия магнитного момента , помещенного в магнитное поле с индукцией , можно определить по формуле . При этом на магнитный момент действует сила 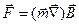и момент сил .