Главная | Обратная связь

Сила Лоренца. Сила Ампера.

Рассмотрим взаимодействие зарядов в системе координат К¢, движущейся относительно системы К со скоростью v в направлении положительных значений оси X.

В общем случае проекции сил в различных системах координат не равны между собой. Однако, между ними имеются определенные соотношения, обеспечивающие инвариантность уравнений движения, т.е. их одинаковый вид в различных системах координат

dp_x/dt = F_x, dp_y/dt = F_y , dp_z/dt = F_z (9.1)

dp_x¢/dt¢ = F_x¢, dp_y¢/dt¢ = F_y¢, dp_z¢/dt¢ = F_z¢. (9.2)

Левые части этих уравнений преобразуем с помощью формул теории относительности для импульса и преобразований Лоренца

p_y = p_y¢ p_z = p_z¢ (9.3)

Где E= m¢c² –полная энергия материальной точки, β=v/c.

Формулы приводятся к виду

F_x =dp_x/dt =(dp_x/dt¢) (dt¢/dt)= =

= F_x¢ + + 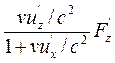(9.4)

F_y =dp_y/dt = (dp_y/dt¢) (dt¢/dt) = (9.5)

F_z =dp_z/dt = (dp_z/dt¢) (dt¢/dt) = (9.6)

Где u_x¢, u_y¢, u_z¢ - скорости точки в системе K¢; F_x¢, F_y¢, F_z¢ вошли в правые части уравнений в результате использования уравнений движения (9.2). При вычислении(9.4) принята во внимание формула

dE¢/dt¢ = F¢u¢ (9.7)

выражающая закон сохранения энергии в системе координат K¢. С помощью формул сложения скоростей

(9.8)

Выражение (9.4) приведем к виду

F_x = F_x¢ + 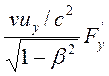+ (9.9)

Для упрощения (9.5) и (9.6) необходимо важное соотношение, которое получается из формул для преобразования скоростей. Запишем прямые и обратные преобразования, например, у-проекции скорости

Перемножая почленно левые и правые части этих равенств и сокращая полученные равенства на общий множитель u_уu_y¢ находим

(1+v u_x¢/c²)/(1-v u_x/c²)=1-β². (9.10)

Учитывая (9.10), преобразуем формулы (9.5) и (9.6)

F_y = (9.11)

F_z = (9.12)

Таким образом, с помощью формул (9.9), (9.10) и (9.12) сила в системе координат К выражена через силу в системе К¢. По принципу относительности можно написать и обратные преобразования.

Запишем формулы преобразования сил в векторной форме. Введем обозначения

Z= (F_x¢, F_y¢/Ö1-β², F_z¢/Ö1-β²) (9.13)

G=[0, - (v/c²) F_z¢/Ö1-β²), (v/c²) F_x¢/Ö1-β²)] (9.14)

Нетрудно проверить, что с помощью (9.13) и (9.14) формулы (9.9) (9.11) и (9.12) записываются в виде векторного равенства

F =Z + u×G(9.15)

Так какF – вектор, то и вся правая часть-вектор. Равенство справедливо для произвольныхu. Следовательно, каждое из слагаемых в правой части является вектором. Поскольку

u×Gиu –векторы, то и Gтоже вектор. Таким образом, определяемые равенствами (9.13) и (9.14) величины Z и G являются векторами.

Сила Лоренца.

Положим, что в системе координат K¢ имеется только электрическое поле и, следовательно, сила (F_x¢ F_y¢ F_z¢) не зависит от скорости u¢ частицы. Тогда Z не зависит от скорости частицыuчастицы и представляет собой электрическую силу в системе координатK.

Аналогично вектор G также не зависит от скорости u частицы, а может зависеть лишь от координаты и времени. Поэтому зависимость силы от скорости частицы содержится во втором слагаемом (9.15)

F = u×G

Это магнитная сила, направленная перпендикулярно скорости частицы и вектору G, представляющему магнитное поле, которое действует на движущуюся частицу. Поскольку Zв формуле (9.15) представляет электрическую силу, действующую на заряд q, то напряженность

Е = Z/q

Аналогично индукция магнитного поля

B =G/q

С учетом предыдущих формул, сила, действующая на заряд, записывается в форме

F= qE+qu×B

Это сила Лоренца. Первое слагаемое определяет силу электрического взаимодействия, второе – действие магнитного поля.

 

 

МАГНЕТИЗМ

ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ЗАРЯДЫ И ТОКИ

5.1. Сила Лоренца

 

Магнитное поле - это особый вид материи. Подобно тому, как элек­трическое поле проявляет себя действием на заряды, магнитное поле проявляется в том, что на движущиеся заряды и электрические токи в этом поле действуют силы. Количественной характеристикой магнитно­го поля служит вектор магнитной индукции В. Если в пространстве существует магнитное поле, то в каждой его точке Р(r)имеется вектор В, который может изменяться с течением времени:

(5.1)

В = B(t,r).

Магнитное поле называется постоянным, когда магнитная индукция В

от времени не зависит. Если вектор Вне зависит от радиус-вектора r, то магнитное поле называется однородным (рис. 5.1).

 

Опытным путем была установлена формула, которая описывает дей­ствие магнитного поля на движущийся со скоростью vэлектрический за­ряд q. Сила, с которой магнитное поле действует на движущийся заряд, называется силой Лоренца. Эта сила коллинеарна векторному произве­дению вектора скорости на вектор магнитной индукции:

 

(5.2)

По определению векторного произве­дения модуль силы Лоренца

F = | q | v В sin a , (5.3)

где а - угол между векторами vи В . Формулу (5.2) можно рассматривать как определение вектора магнитной индукции. Единицей измерения магнитной индукции в СИ служит тесла (T): [В] = Т = Н с/(Кл м) = кг/(с²А).

Согласно формуле (5.2) сила Лоренца, действующая на заряд в маг­нитном поле, перпендикулярна и вектору скорости vзаряда, и вектору Виндукции магнитного поля (рис. 5.2). При этом скалярное произве­дение вектора скорости на вектор силы Лоренца,

vF =0,

т.е. мощность силы Лоренца равна нулю. Отсюда следует, что сила Лоренца работу не совершает и кинетическая энергия частицы при ее движении в магнитном поле со временем не изменяется.

 

 

Рис. 5.2. Сила Лоренца

5.2. Движение заряженной частицы в однородном и постоянном магнитном поле

Пусть в пространстве существует однородное и постоянное магнитное поле. Такое поле характеризуется в любой точке пространства одним и

тем же вектором В . Построим систему координат так, чтобы ось у совпа­дала по направлению с вектором Вмагнитной индукции. При этом две проекции В_х и В_z вектора Вбудут равны нулю: В{0, В, 0}. Исследуем движение заряженной частицы в таком

Запишем второй закон Ньютона:

mv = q [ v В] , (5.4)

где m, q - масса и заряд частицы.

Проекции вектора [v В] на оси координат можно найти по известному правилу из векторной алгебры:

 

= =

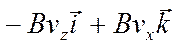
При помощи этого выражения запишем второй закон Ньютона в проек­циях на оси координат:

mv_x¢ = - q В v_z , т v_y¢ = 0 , mv_z¢ = q В v_x . (5.5)

Решив эту систему уравнений, можно найти при заданных начальных условиях зависимость от времени вектора скорости частицы: v = v(t), a затем из уравнения r¢ = v - зависимость r = r(t), описывающую движение частицы.

Задача. Решить систему уравнений (5.5). Найти зависимость r = r(t) при произвольных начальных условиях. Показать, что траекто­рией движения заряда в магнитном поле является винтовая линия.

Согласно формуле (5.2) сила Лоренца равна нулю, когда вектор скоро­сти коллинеарен вектору магнитной индукции. Поэтому вдоль силовой линии однородного магнитного поля заряженная частица движется равномерно и прямолинейно:

F = 0 , v = const .

Направим ось у вдоль силовых линий магнитного поля (рис. 5.3). В
таком случае координата у заряженной частицы будет изменяться со
временем по закону

y(t)=y₀+vt

Рис.5.3. Вдоль силовой линии однородного магнитного поля заряженная частица движется равномерно и прямолинейно

 

Пусть в начальный момент времени t = 0 скорость заряда была пер­пендикулярна вектору В : v_y(0) = 0. При этом из второго уравнения системы (5.5) следует, что v_y(t) = 0, т.е. частица все время будет дви­гаться в плоскости перпендикулярной вектору В: v^ В . Так как сила Лоренца работу не совершает и кинетическая энергия частицы со вре­менем не изменяется, модуль вектора скорости также постоянен. В этом случае тангенциальное ускорение а_т = v¢ будет равно нулю, а нормальное ускорение в силу второго закона Ньютона будет

а_п =|q|vB/m

В

(5.6)

 

 

Рис. 5.4- Когда скорость за­ряженной частицы перпенди­кулярна силовым линиям одно­родного магнитного поля, она движется по окружности

 

Видно, что в постоянном и однород­ном магнитном поле нормальное уско­рение заряженной частицы со

време­нем не изменяется. Это означает, что частица будет двигаться по окружно­сти (рис. 5.4). Радиус

R этой окруж­ности найдем при помощи формулы для центростремительного ускорения

 

а_п =v²/R (5.7)

Приравняем правые части равенств (5.6) и (5.7). Получим:

R= т v/(|q|B)

В общем случае заряженная частица в однородном магнитном поле мо­жет совершать два вида движений. Во-первых, частица может двигаться равномерно с некоторой скоростью v||_ вдоль прямой, которая является силовой линией магнитного поля. Во-вторых, частица может двигаться с постоянной скоростью v^_ по окружности, которая расположена в плос­кости, к которой силовые линии магнитного поля перпендикулярны. Эти два движения частица может совершать одновременно. В таком случае траекторией движения частицы будет винтовая линия (рис. 5.5). Эта линия характеризуется такими параметрами, как радиус R и шаг h, т.е. наименьшее расстояние между двумя точками на этой линии, отсчитан­ное вдоль ее оси. При этом проекции v||_ и v^_ вектора скорости v будут связаны с его модулем и углом а между ним и вектором Всоотношени­ями

v|| = v cos a , v^ = v sin a .

 

Время Т, за которое частица совершает один оборот по винтовой ли­нии, называется периодом обращения. За это время, двигаясь по окруж­ности со скоростью v^, она пройдет путь 2pR, а при движении вдоль силовой линии со скоростью v|| - путь h:

2p R = v^ Т, h = v|| Т .

Радиус R винтовой линии связан со скоростью v± соотношением

R=m v^//(|q|B)

 

V

Рис. 5.5. Траектория движения заряженной частицы в однородном и постоянном магнитном поле - винтовая линия

5.3. Действие магнитного поля на проводник с током. Сила Ампера

Рассмотрим прямолинейный участок проводника с током, помещенно­го в пространстве, где имеется однородное магнитное поле. Электриче­ский ток есть направленное движение заряженных частиц, называемых носителями тока. На движущийся в магнитном поле заряд действует сила Лоренца.

Сумма всех сил Лоренца, которые действуют на носители тока в проводнике, может быть преобразована к виду(5.8)

 

 

(5.8)

где I - сила тока, текущего в проводнике; l - вектор, направление которо­го совпадает с направлением тока, а модуль равен длине l рассматрива­емого участка проводника (рис. 5.6). Сила F, определяемая формулой (5.8), называется силой Ампера. Согласно определению векторного про­изведения сила Ампера перпендикулярна векторам l и В, а ее модуль

F= IlВ sin a ,

где а - угол между векторами l и В . Сила Ампера не приложена к какой-либо точке проводника, а распределена по его объему.

Формулы (5.8) и (5.9) справедливы только в том случае, когда прямой проводник находится в однородном магнитном поле. Чтобы найти в об­щем случае силу, которая действует на тонкий провод с током в магнит­ном поле, разделим его на небольшие участки. Каждый такой участок можно считать прямолинейным, а магнитное поле в нем - однородным.

По формуле (5.8) найдем силу Ампера dF , которая действует на один из участков провода:

(5.10)

 

где dl - векторный элемент участка провода. Сила, с которой магнит­ное поле действует на тонкий провод с током, равна криволинейному интегралу

 

 

Рис. 5.6. Сила Ампера

 

 

ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ЗАРЯДЫ И ТОКИ (продолжение)