Главная | Обратная связь

Ротор. Теорема Стокса.

 

Если в движущеёся жидкости с распределением скоростей от до выделить контур Г, а остальную жидкость мгновенно заморозить, то в этом контуре будет продолжаться движение жидкости. Мерой такого действия является произведение скорости жидкости в контуре на длину контура. Эту величину называют циркуляцией вектора по контуру Г.

Циркуляция =

Циркуляция обладает свойством аддитивности, т.е. циркуляция по контуру Г будет равна сумме циркуляций по контурам Г₁ и Г_2.

Благодаря такому свойству можно ввести понятие удельной циркуляции в точке Р – это векторная величина, называемая ротором или вихрем.

 

 

Рис. 6.14- К выводу теоремы Стокса

 

Рассмотрим циркуляцию по элементарному квадрату в декартовой системе координат.

Знак минус ставится тогда, когда направления c_x не совпадает с направлением обхода.

Учитывая, что , получим:

Аналогично для сторон квадрата 2 и 4:

,

Тогда циркуляция по квадрату будет равна:

, где S – площадь квадрата.

Разделив циркуляцию на , найдём проекции на оси координат:

(1*)

(2*)

(3*)

Любое из выражений (1*) - (3*) можно получить из предыдущего путём циклической системы координат.

Для уравнения (1*) предыдущим является уравнение (3*). Таким образом, ротор вектора в декартовой системе координат будет иметь вид:

Если известно, что ротор каждой точки поверхности S охватывается контуром Г, то можно вычислить и циркуляцию по этому контуру:

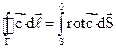
Теорема Стокса: циркуляция вектора по замкнутому контуру равна потоку вектора rot через площадку S, ограниченную этим контуром.

Отметим, что

Мы рассмотрим три вида сочетаний, в которые входит оператор (набла)

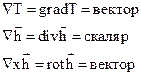
Используя эти сочетания, можно пространственные вариации полей записать в виде независимых от той или иной совокупности осей координат.

Формула Стокса.

 

По определению ротор (вихрь) некоторого вектора :

 

(36)

 

Зная ротор вектора в каждой точке некоторой (не обязательно плоской) поверхности S, можно вычислить циркуляцию этого вектора по контуру , ограничивающему S, (контур также может быть не плоским). Для этого разобъём поверхность на очень малые элементы . Ввиду их малости эти элементы можно считать плоскими. Поэтому в соответствии с (36) циркуляция вектора по контуру, ограничивающему , может быть представлена в виде.

 

(37)

 

где - положительная нормаль к элементу поверхности .

 

Зная, что циркуляция по некоторому контуру равна сумме циркуляций по контурам, содержащиеся в данном, можно просуммировать выражение (37) по всем , и тогда получим циркуляцию вектора по контуру , ограничивающему S:

 

.

 

Осуществив предельный переход, при котором все стремиться к нулю (число их при этом неограниченно растёт, придём к формуле:

 

(38)

Соотношение (38) носит название теоремы Стокса. Смысл её состоит в том, что циркуляция вектора по произвольному контуру равна потоку вектора через произвольную поверхность S , ограниченную данным контуром.

 

Теорема Стокса

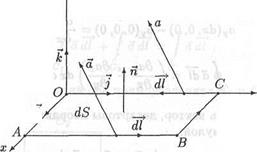
Пусть в пространстве задано векторное поле а — а(г). Построим не­которую поверхность и вырежем из нее посредством контура С часть S (рис. 6.5). Про эту часть поверхности говорят, что она натянута на кон­тур С. Про контур С можно сказать, что он ограничивает поверхность 5. Вырежем из поверхности 5 бесконечно малый прямоугольник площадью dS. Построим декартову прямоугольную систему координат так, чтобы ее начало О совпало с одной из вершин прямоугольника, а координат­ные оси х и у проходили через его стороны (рис. 6.14). Другие вершины прямоугольника обозначим А, В и С. Пусть стороны О А и ВС этого прямоугольника, параллельные оси х, равны dx, а стороны АС и СО, параллельные оси у, - dy. При этом вершины прямоугольника будут иметь следующие координаты:

A(dx,0,0), B(dx,dy,O), C(O,dy,O).

sin a da

(6.36) Для бесконечного провода а\ = 0 и (6.36) принимает вид

Вычислим циркуляцию

ladf

вектора а по контуру С\ = ОАВСО. Направим нормаль п к плоскости прямоугольника С\ вдоль оси z

где к - единичный орт, направленный вдоль оси z. элемент поверхности будет

dS = dx dy - площадь прямоугольника.

z k■

Рис. 6.14- К выводу теоремы Стокса

Будем обходить контур С\ так, чтобы направление обхода, т.е. напра­вление векторов dl , было связано с направлением нормали п правилом правого винта. В таком случае векторный элемент контура будет

dl = Циркуляция вектора а по прямоугольнику С\ равна сумме криволи­нейных интегралов по его сторонам:

dx г на О А ,

dy j на АВ ,

— dx -г на ВС ,

-dy- j на СО.

-dy- j на СО

dS = dx dy - площадь прямоугольника.

z k

■ ■

Так как стороны прямоугольника С\ бесконечно малы, эти интегралы с большой точностью будут равны следующим произведениям:

/ аЖ = а_х(0, 0, O)dx, I аЖ = a_y(dx, О, 0) dx ,

ОА

А АВ

аЖ = -а_х(0, dy, 0)dx, f аЖ = - а_у(0, О, 0)dx .

Подстановка этих произведений в формулу (6.38) дает 1аЖ= - (а_х(0, dy, 0) - а_х(0, 0, 0)) dx + (a_y(dx, 0, 0) - а„(0, 0, 0)) dy.

-»w- a,(0, dy, 0) - o_e(0, 0, 0) = -~ dy, > ,., t

a,,(efa, 0, 0) - а„(0, 0, 0) = -£*- dx ,

да_ч да_х

дх ду

Ротор вектора а есть вектор, декартовы координаты которого опреде­лены следующей формулой:

i j к

д_ д_ д_

дх ду dz

а_х а_у a_z

Согласно этой формуле проекция вектора rot а на ось z будет

да,, да (rota)* = -г. 9z ду

Теперь с учетом формулы (6.37) выражение (6.39) можно записать так:

1аЖ = rota dl . (6.40)

Таким образом, циркуляция вектора а по бесконечно малому прямо­
угольному контуру С\ равна потоку ротора rot а вектора а через плос­
кость, ограниченную этим прямоугольником.

Произвольную поверхность S можно разрезать на множество бесконеч­но малых прямоугольников С{. Докажем, что сумма циркуляции вектора а по этим прямоугольникам равна циркуляции вектора а по контуру С, который ограничивает поверхность S (рис. 6.5):

Так как получим rot a = dxdy

rot a =

2 Ф Sdl = Ф a dl

Рассмотрим два соприкасающихся прямоугольника С\ и Съ (рис. 6.15, а). Криволинейные интегралы

по совпадающим участкам контуров равны по абсолютной величине и противоположны по знаку. Поэтому их сумма равна нулю. Следова­тельно, справедливо равенство

I аЖ + IаЖ = I аЖ ,

где С - контур, огибающий оба прямоугольника С\ и Сг (рис. 6.15, б").

С₂

■

A a) ^iVL б)

Рис. 6.15. К выводу теоремы Стокса ц

Аналогично, в левой части равенства (6.41) взаимно уничтожаются криволинейные интегралы по совпадающим участкам прямоугольников и остается только интеграл по кривой С, окаймляющей поверхность S. Согласно соотношению (6.40) каждое слагаемое в левой части равенства (6.41) равно элементарному потоку вектора rot а через поверхность dSi, ограниченную прямоугольником С». Так как поверхность dSi есть эле­мент поверхности S, левая часть равенства (6.41) будет равна полному потоку вектора rot а через поверхность S. Таким образом, доказана те­орема Стокса:

(6.42)

Согласно этой теореме циркуляция вектора а по произвольному замкну­тому контуру С равна потоку ротора этого вектора через произвольную поверхность S, натянутую на этот контур (рис. 6.5), при условии, что направление обхода контура (т.е. направление вектора dl) связано с направлением нормали п к поверхности S правилом правого винта.