Главная | Обратная связь

Формула Остроградского – Гаусса.

 

Пусть f (x, y, z) - некоторая функция , а S - замкнутая поверхность, ограничивающая объём V. На отрезке 1-2 (рис. 4), параллельном оси X, f - является функцией одного аргумента x. Интегрируя вдоль этого отрезка получим:

 

 

где 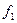и - значения функции f на концах рассматриваемого промежутка.

Построим теперь бесконечно узкий цилиндр, одной из образующих которого является отрезок 1 2. Пусть dσ - площадь поперечного сечения его (величина положительная). Умножая предыдущее соотношение на dσ. Так как dσdx есть элементарный объём dV,заштрихованный на рисунке, то в результате получится:

,

 

где dV – часть объёма V, вырезаемого из него поверхность цилиндра. Пусть dS₁ и dS₂ эле -ментарные площадки, вырезаемые тем же цилиндром на поверхности S, а ₁ и ₂–

единичные нормали к ним, проведенные наружу от поверхности S. Тогда:

dσ = d _{2 2х} = - d _{1 1х},

 

а поэтому:

или короче: где поверхностный интеграл распространён на сумму площадок dS₁ и dS₂. Весь объём V можно разделить на элементарные цилиндры рассматриваемого вида и написать для каждого из них такие же соотношения. Суммируя эти соотношения, получим:

(35)

 

Интеграл справа распространён по всему объёму V, справа – по поверхности S, ограничивающей этот объём. Аналогичные соотношения можно написать для осей Y и Z.

Возьмём теперь произвольный вектор и применим к его компонентам соотношение (35). Получим:

 

и аналогично для компонент A_y и A_z . Складывая эти соотношения, найдём:

 

 

или:

 

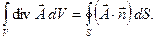
Эту формулу Остроградского – Гаусса можно также записать в виде:

 

 

Смысл её заключается в том, что полный поток вектора через некоторую поверхность S равен суммарной алгебраической мощности источников, порождающих векторное поле.

Если объём V бесконечно мал, то величина div внутри него может считаться постоянной. Вынося её за знак интеграла и переходя к пределу V→ 0, получим:

 

 

Предельный переход надо понимать в том смысле, что область V должна стягиваться в точку, т.е. размеры этой области должны беспредельно уменьшаться по всем направлениям. Эти рассуждения показывают, что величина, стоящая в правой части вышеуказанной формулы, не зависит от формы поверхности S, стягиваемой в точку. Поэтому это выражение можно принять за исходную формулировку дивергенции. Такое определение обладает преимуществом, потому что оно инвариантно, т.е. никак не связано с выбором координат.

 

Формула Стокса.

 

По определению ротор (вихрь) некоторого вектора :

 

(36)

 

Зная ротор вектора в каждой точке некоторой (не обязательно плоской) поверхности S, можно вычислить циркуляцию этого вектора по контуру , ограничивающему S, (контур также может быть не плоским). Для этого разобъём поверхность на очень малые элементы . Ввиду их малости эти элементы можно считать плоскими. Поэтому в соответствии с (36) циркуляция вектора по контуру, ограничивающему , может быть представлена в виде.

 

(37)

 

где - положительная нормаль к элементу поверхности .

 

Зная, что циркуляция по некоторому контуру равна сумме циркуляций по контурам, содержащиеся в данном, можно просуммировать выражение (37) по всем , и тогда получим циркуляцию вектора по контуру , ограничивающему S:

 

.

 

Осуществив предельный переход, при котором все стремиться к нулю (число их при этом неограниченно растёт, придём к формуле:

 

(38)

Соотношение (38) носит название теоремы Стокса. Смысл её состоит в том, что циркуляция вектора по произвольному контуру равна потоку вектора через произвольную поверхность S , ограниченную данным контуром.

 

 

Дополнения