 |
|
Марковские случайные процессы
Изучение производственных процессов часто требует построения математической модели, которая бы с достаточной степенью адекватности описывала этот процесс.
В большинстве случаев не удается построить простую математическую модель, позволяющую в явном виде найти интересующие нас величины в зависимости от изменяющихся условий и элементов решения.
Однако иногда такую модель построить можно, в том случае если исследуемая операция может быть представлена как марковский случайный процесс.
Случайный процесс, протекающий в системе, называется марковским, если для любого момента времени t0 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t0 и не зависят от того, когда и как система пришла в это состояние.
Большое значение имеют марковские случайные процессы с дискретными состояниями и непрерывным временем. Для таких процессов все возможные состояния S1, S2, S3,… можно перечислить, и переход системы из одного состояния в другое происходит «скачком». Моменты возможных переходов из состояния в состояние неопределенны, случайны, т.е. переход может произойти, в принципе, в любой момент.
При анализе случайных процессов с дискретными состояниями удобно пользоваться геометрической схемой – графом состояний. Состояния обозначаются прямоугольниками, а возможные переходы из состояния в состояние – стрелками, соединяющими эти состояния.
Переход системы из одного состояния в другое происходит под воздействием потока событий.
Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.
Интенсивность потока событий  - среднее число событий, приходящееся на единицу времени.
- среднее число событий, приходящееся на единицу времени.
Поток событий называется регулярным, если события следуют одно за другим через определенные, равные промежутки времени.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, для стационарного потока  .
.
Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга, вызванные своими собственными причинами.
Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по несколько сразу.
Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами: стационарен, ординарен и не имеет последействия.
Для наглядности удобно на графе состояний у каждой стрелки проставлять интенсивность того потока событий, который переводит систему по данной стрелке. Интенсивность потока событий, переводящего систему из состояния Si в Sj, обозначается  . (рис. 1).
. (рис. 1).
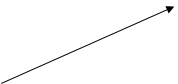
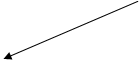


 S1
S1
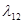
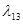
 |  |
 S2 S3
S2 S3






S4
Рис. 1
Для любого момента сумма всех вероятностей состояний равна единице:  .
.
Имея размеченный граф состояний, можно найти все вероятности состояний Pi(t) как функции времени. Для этого составляются и решаются уравнения Колмогорова.
Сформулируем общее правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности какого-то (i-го) состояния. В правой части – сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го) состояния.
Например, для графа, показанного на рис. 2 уравнения Колмогорова будут иметь следующий вид:

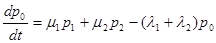 ,
,
 ,
,
 ,
,
 .
.



 S0
S0 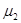


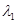



S1 S2




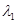
|


Рис. 2
Для решения уравнений Колмогорова задаются начальными условиями. Если точно известно начальное состояние системы Si, то в начальный момент (при t=0) Pi(0) = 1, а все остальные начальные вероятности равны нулю.
Если число n состояний системы конечно и из каждого из них можно за конечное число шагов перейти в любое другое, то говорят о существовании предельных (финальных) вероятностей.
При  в системе S устанавливается предельный стационарный режим, в ходе которого система случайным образом меняет свои состояния, но их вероятности уже не зависят от времени. Можно сказать, что предельная вероятность состояния Si – это среднее относительное время пребывания системы в этом состоянии.
в системе S устанавливается предельный стационарный режим, в ходе которого система случайным образом меняет свои состояния, но их вероятности уже не зависят от времени. Можно сказать, что предельная вероятность состояния Si – это среднее относительное время пребывания системы в этом состоянии.
Поскольку для постоянных значений вероятностей их производные равны нулю, то чтобы найти предельные вероятности, нужно все левые части уравнениях Колмогорова приравнять к нулю и решить получившуюся систему линейных уравнений.
При этом любое из уравнений получившейся системы отбрасывается и вместо него используется уравнение нормировки: P0+P1+P2+…+Pn = 1.