Способи задання функції

Функцію двох змінних, як і функцію однієї змінної, можна подати такими способами:

· аналітично(у вигляді формули); наприклад:

· таблично; наприклад:

х	у

(таблиця множення чисел: z = xy)

· графічно(рис. 1.7);

Рис. 1.7

1.1.5. Графічне зображення функції
двох змінних

Означення. Графікомфункції двох змінних називається множина всіх точок (х, у, f(x, y)) простору R³, де (x, y) Î R².

Щоб зобразити графічно функцію двох змінних, розглянемо систему координат хуz у тривимірному просторі (рис. 1.8).

Рис. 1.8

Кожній парі чисел х і у відповідає точка Р(х, у) площини ху. Узявши в цій точці значення функції 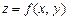, дістанемо точку у просторі R³ з координатами (х, у, z), яка позначається символом Q(х, у, z). Усі такі точки, що відповідають різним значенням незалежних змінних х і у, утворюють певну поверхню у просторі R³. Ця поверхня і є графічн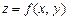им зображенням функції .

Графічним зображенням функції є площина, що проходить через точки (0, 0, 4), (0, 4, 0), (4, 0, 0) (рис. 1.9).

Рис. 1.9

Графічним зображенням функції є сідло (рис. 1.10).

Рис. 1.10

Зауваження. На практиці побудувати графік функції двох змінних буває нелегко, оскільки потрібно зобразити на площині просторову фігуру, а це не завжди вдається.

Існує й інший спосіб геометричного зображення функції двох змінних — за допомогою ліній рівня.

Означення. Лінією рівняназивається множина всіх точок площини, в яких функція 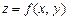набуває однакових значень. Рівняння ліній рівня записують у вигляді . Для функції трьох змінних розглядають поверхні рівня.

Накресливши кілька ліній рівня та задавши значення на них функції, дістанемо певне уявлення про характер зміни функції.

Один з найпростіших прикладів зображення функції за допомогою ліній рівня — задання рельєфу місцевості на географічній карті. Висота місцевості над рівнем моря є функцією координат точки земної поверхні. За лініями однакової висоти, нанесеними на карту, легко уявити рельєф відповідної місцевості.

У метеорології лініями рівня є ізотермита ізобари. В економіці — ізокванти, криві індиферентності. Лініями рівня виробничої функції є ізокванти. Ізокванта— крива, утворена множиною точок, що відповідають різним варіан-
там поєднання двох будь-яких видів витрат, котрі забезпечу-
ють постійно одну й ту саму кількість виготовлюваної продукції (рис. 1.11). Крива індиферентностівідбиває зміну поєднання двох різних благ за умови, що загальна споживна корисність їх лишається сталою (рис. 1.12).

Рис. 1.11 Рис. 1.12

Побудувати лінії рівня функції

●Шукане рівняння має вигляд

1. Якщо с < 0, то ліній рівня немає.

2. Якщо с = 0, то лінії рівня становлять множину всіх точок осі х, крім двох: (± 2, 0).

3. Якщо с > 0, маємо
, або . Отже, лініями рівня є кола радіусом із центром у точці , з яких вилучено точки (± 2, 0). Узявши с = 1, 2, …, дістанемо сім’ю ліній рівня (рис. 1.13).

Рис. 1.13

1.1.6. Знаходження області визначення функції двох змінних

Розглянемо алгоритм знаходження області визначення функції двох змінних на такому прикладі.

Знайти область визначення функції

та надати відповідну геометричну інтерпретацію.

1. Запишемо область визначення функції аналітично:

2. Замінивши нерівності в D рівностями, побудуємо лінії, що відповідають їм на координатній площині:

3. За допомогою контрольних точок і з’ясуємо розміщення D на площині й виділимо її штриховкою (рис. 1.14).

Рис. 1.14

1.1.7. Границя функції двох змінних

Означення. Число А називається границею функції при , , якщо для будь-якого існує число 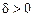, таке, що в разі виконання нерівності

справджується нерівність .

Позначають:

або

Наслідок.

Теорема 1.1. Якщо функція f(х, y) має границю при (х, y) ® ® (х₀, y₀), то така границя тільки одна.

Теорема 1.2. Якщо функція f(х, y) має границю при (х, y) ®
® (х₀, y₀), то вона обмежена в деякому околі точки f(х₀, y₀).

Теорема 1.3. Якщо , і в деякому виколотому околі точки ( , y₀) виконується нерівність , то .

Наслідок.Якщо у деякому околі точки ( , y₀) і 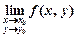існує, то ця границя невід’ємна (недодатна).

Теорема 1.4. Якщо і в деякому виколотому d-околі точки ( , y₀) справджуються нерівності , то і .

Теорема 1.5. Якщо ,

то виконуються рівності:

1) ;

2) ;

3) (с ¹ 0).

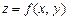Означення.Якщо , то функція називається нескінченно малоюпри

Обчислити .

●Застосувавши теорему 1.5 про арифметичні операції над границями, а також узявши до уваги те, що границя сталої величини дорівнює цій сталій, тобто

дістанемо:

Обчислити .

●Візьмемо ху = t. Тоді з того, що (х, у) ® (0, 0), випливає t ® 0 і задану границю можна подати у вигляді 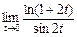. При t ® 0 маємо: , . Отже,

Звідси, .

Зауваження. Поняття границі в точці для функції однієї змінної та функції багатьох змінних мають багато спільного, але існує й принципова різниця, з огляду на яку поняття границі функції кількох змінних є істотно більш обмеженим, ніж поняття границі функції однієї змінної.

Так, для функції багатьох змінних справджуються теореми про границю суми, добутку та частки, які аналогічні відповідним теоремам для функції однієї змінної.

Водночас маємо такі розбіжності між цими поняттями:

Якщо (f(x) — функція однієї змінної), то це означає, що і лівостороння і правостороння границі її дорівнюють b. Обернене твердження також правильне: з існування та збігу двох односторонніх границь випливає існування границі функції в
точці.

Для функції двох змінних 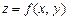наближення до точ-
ки (х₀, у₀) можливе нескінченною кількістю способів: і спра-
ва, і зліва, і згори, і знизу, і під деяким кутом до осі х тощо (рис. 1.15).

Більш того, до точки можна наближатися не лише по прямій, а й по складніших траєкторіях (рис. 1.16).

Рис. 1.15 Рис. 1.16

Очевидно, що рівність справджується тоді й тільки тоді, коли границя досягається в результаті наближення до точки (х₀, у₀) по будь-якій траєкторії. Отже, маємо істотне обмеження порівняно зі збігом двох односторонніх границь у разі функції однієї змінної.

Довести, що не існує.

· Наближатимемося до точки (0, 0) по прямій у = kx.

Якщо у = kx, то

Зауважимо, що значення границі залежить від кутового коефіцієнта прямої, наприклад:

при k = 1 границя дорівнює ,

при k = 2 границя дорівнює і т. д.

Отже, наближаючись до точки (0, 0) у різних напрямах, дістаємо різні границі. Це означає, що не існує.

Зауваження. Для функцій n > 1 змінних можна розглядати n! так званих повторних границь.

У частинному випадку для функції двох змінних можна розглядати дві повторні границі в точці (х₀, у₀):

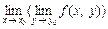і .

Наприклад, для функції маємо:

Отже, змінювати порядок граничних переходів загалом не можна.

Скажімо, у попередньому прикладі не існує, але повторні границі існують: .

1.1.8. Неперервність функції двох змінних

Означення. Функція називається неперервною в точці , якщо

Означення. Функція називається неперервною в області(замкненій чи відкритій), якщо вона неперервна в кожній точці цієї області.

Означення. Функцію 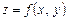, визначену на множині D Ì R², називають неперервною за множиною Е Ì D в точці (х₀, у₀) D,якщо

Означення. Точка називається точкою розриву функції , якщо:

1) функція не визначена в точці ;

2) функція визначена в точці , проте:

а) не існує;

б) існує, але не дорівнює .

Означення. Точка називається точкою усувного розривуфункції , якщо існує, але або не визначена в точці , або

Розглянемо функцію двох незалежних змінних

Ця функція має розрив у точці (0, 0), бо в ній для функції границі не існує.

Тут ми стикаємося з цікавим явищем: розглядувана функція не є неперервною в точці (0, 0) за двома змінними водночас, але є неперервною за кожною зі змінних х і у окремо.

Точки розриву можуть бути не лише ізольованими, як у попередньому прикладі, а можуть заповнювати
лінії, поверхні тощо. Так, функції двох змінних , мають розриви: перша — прямі друга — окіл Для функції трьох змінних

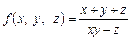розриви заповнюють відповідно гіперболічний параболоїд і конус

Знайти

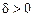●Для будь-якого існує , таке що для всіх точок , які задовольняють умову і відмінні від початку координат, справджується нерівність

Отже,

Знайти границю функції

в точці (0, 0) за множиною, на якій функція визначена.

●Зауважимо, що функція не визначена в точках прямої . Тому звичайної границі в точці (0, 0) не існує. Але границя за множиною точок , на якій функція визначена, існує і дорівнює нулю, оскільки

Знайти значення а, при якому функція

в точці (0, 0):

1) є неперервною за прямою , , ;

2) неперервною за кривою ;

3) неперервною.

●1. Наближатимемося до точки (0, 0) по прямій , , . Це означає, що виконуються рівності:

Якщо 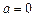, то дана функція буде неперервною за даною прямою.

2. Наближатимемося до точки (0, 0) по кривій :

Якщо , то розглядувана функція буде неперервною за даною прямою.

3. У точці (0, 0) функція має розрив, оскільки в ній границя не існує. Це випливає з 1 і 2.

Знайти точки розриву, а також точки усувного розриву функції двох змінних:

1) ;

2) .

●1. Функція в точці (0, 0) не існує, тому вона має в цій точці розрив. Знайдемо границю

Для будь-якого існує , таке що для всіх точок , які задовольняють умову і відмінні від початку координат, виконується нерівність

Отже, і функція має в точці (0, 0) усувний розрив, якщо у цій точці.

2. Функція не існує, якщо , тобто , , .

Тому вона має розриви. Знайдемо границю

Отже, функція має в точці неусувний розрив.

1.1.9. Неперервність складеної
(складної) функції двох змінних

Означення.Нехай функція визначена на множині Е, а змінні і , у свою чергу, залежать від змінних х і у: причому обидві функції та визначені на множині D. Якщо для будь-якого існує значення (рис. 1.17), то говорять, що на множині визначено складену (складну) функцію де — проміжні, х, у — незалежні змінні.

Рис. 1.17

Функція де . Це складена функція, яка визначена на координатній площині. Її можна записати у вигляді

Теорема 1.6. Нехай на множині D визначено складену функцію , де , і нехай функції , неперервні в точці , а функція неперервна в точці , де , . Тоді складена функція неперервна в точці .

Доведення. За умовою теореми функція неперервна. За означенням неперервності функції в точці візьмемо довільне число , тоді існує таке , що з нерівності