Главная | Обратная связь

Движение жидкой линии или жидкой поверхности

Задачу о продвижении границы раздела, когда μ₁≠μ₂, будем решать приближенно.С этой целью, исходя из физической природы вытеснения одной жидкости другой из пористой среды, сделаем ряд допущений.

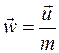Вследствие неравномерного распределения размеров поровых каналов действительные скорости частиц жидкости распределены неравномерно. Поэтому в рассматриваемых ниже задачах определяются расчетные средние действительные скорости частиц в сечениях элементарных трубок тока, связанные со скоростью фильтрации соотношением , где m— пористость. По этим скоростям и будет производиться в дальнейшем расчет движения отмеченных частиц, границы раздела двух жидкостей и т. д. При этом будут получаться принципиально правильные результаты для интегральных характеристик — расходов и средних скоростей. Истинные же скорости частиц могут отличаться от этих средних.

Жидкости предполагаются несмешивающимися, взаимно нерастворимыми и химически не реагирующими одна с другой и с пористой средой. Вытеснение одной жидкости предполагается происходящим полностью — так называемое «поршневое» вытеснение. Это также является идеализацией, так как в действительности полного вытеснения не происходит.

Уравнения движения отмеченных частиц в потоке однородной жидкости.Рассмотрим уравнения движения отмеченных частиц в потоке однородной жидкости.

Пусть дана однородная жидкость, потенциал движения которой Ф(х, у, z, t)известен.

Истинная скорость движения частицы , скорость фильтрации , где ds— элемент траектории.

Тогда уравнения движения могут быть записаны в виде

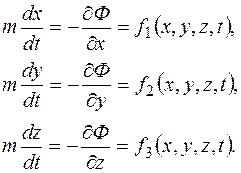(1.1)

Функции f₁, f₂, f₃ известны, поскольку потенциал Ф(х, у, s, t) считается заданным.

Интегрируя систему (1.1), получаем закон движения или траекторию жидкой частицы в виде x = x(t), y = y(t), z = z(t).

Интегрирование производится особенно просто, если скорость есть известная функция одной величины s:

Уравнения движения жидкой линии или жидкой поверхности.Пусть надо найти уравнение жидкой поверхности F(x,у,z,t)=0 при начальном условии

F(x, у, z, 0) = f(x, y, z), (1. 2}

где f(x, y, z)— известная функция.

Проекции перемещения жидкой частицы за время δtбудут где u,v,w — проекции скорости фильтрации на оси х, y, z.

Требуя, чтобы эти частицы остались на жидкой поверхности, имеем

Развертывая это соотношение в ряд Тейлора и удерживая члены с первой степенью δt, получим

откуда, так как F (х, у, z, t) = 0 по условию, устремляя δt к нулю, .получаем

(1.3)

или, заменяя скорости через производные потенциала,

(1.4)

Линейное дифференциальное уравнение в частных производных первого порядка (1.3) представляет собой соотношение Кельвина, выполняющееся на всякой поверхности F (х, у, z, t) = 0, движущейся вместе с жидкостью, т. е. на любой жидкой поверхности.

Требование найти решение уравнения (1.3), удовлетворяющее условию (1. 2), представляет собой задачу Коши для линейного однородного уравнения в частных производных первого порядка.

Система обыкновенных дифференциальных уравнений, соответствующая уравнению (1.3), имеет вид:

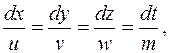(1.5)

причем и, v, w—известные функции координат и времени, так как потенциал скорости Фзадан.