Исследование вынужденных колебаний. Резонанс напряжений.

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

Профессионального образования

НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Заволжский филиал

Кафедра общеобразовательных и общепрофессиональных дисциплин

Исследование электрических колебаний.

Резонанс.

Лабораторная работа №2-3 по общей физике

Заволжье – 2006

Составители: Г.Д. Ботов, Р.В. Бударагин

УДК 537.85

Исследование электрических колебаний. Резонанс.: Лабораторная работа №2-3 по общей физике / НГТУ; Сост.: Г.Д. Ботов и др. Заволжье, 2006.

Дано краткое описание собственных и вынужденных электрических колебаний в колебательном контуре. Представлена экспериментальная установка с использованием системы виртуальных измерений в среде LabVIEW по моделированию и изучению электрических колебаний и порядок работы с ней.

Научный редактор Р.В. Бударагин

ВВЕДЕНИЕ

Целью данной работы является изучение зависимости силы тока в колебательном контуре от частоты источника включенного в контур; измерение резонансной частоты; расчет добротности контура по ширине резонансной кривой.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1. Квазистационарные токи. При рассмотрении электрических колебаний приходится иметь дело с токами, изменяющимися со временем. 3акон Ома и вытекающие из него правила Кирхгофа были установлены для постоянного тока. Однако они остаются справедливыми и для мгновенных значений изменяющихся тока и напряжения, если только их изменение происходит не слишком быстро. Электромагнитные возмущения распространяются по цепи с огромной скоростью, равной скорости света .

Пусть длина цепи равна . Если за время , необходимое для передачи возмущения в самую отдаленную точку цепи, сила тока изменяется незначительно, то мгновенные значения силы тока во всех сечениях цепи будут практически одинаковыми. Токи, удовлетворяющие такому условию, называются квазистационарными. Для периодически изменяющихся токов условие квазистационарности имеет вид , где – период изменений.

Мгновенные значения квазистационарных токов подчиняются закону Ома. Следовательно, для них справедливы и правила Кирхгофа. В дальнейшем при изучении электрических колебаний мы всегда будем предполагать, что рассматриваемые нами токи квазистационарны.

2. Свободные электрические колебания в контуре без активного сопротивления. В цепи, содержащей индуктивность и емкость, могут возникать электрические колебания. Поэтому такая цепь называется колебательным контуром. На рис.1 изображены последовательные стадии колебательного процесса в идеализированном контуре, не обладающем активным сопротивлением.

Колебания в контуре можно вызвать, либо сообщив обкладкам конденсатора некоторый начальный заряд, либо возбудив в индуктивности ток (например, путем включения внешнего магнитного поля, пронизывавшего витки катушки). Воспользуемся первым способом. Присоединим отключенный от индуктивности конденсатор и источнику напряжения. Это приведет и возникновению на обкладках разноименных зарядов и (стадия 1). Между обкладками возникнет электрическое поле, энергия которого равна . Если затем отключить источили напряжения и замкнуть конденсатор на индуктивность, емкость начнет разряжаться и в контуре потечет ток. В результате энергия электрического поля будет уменьшаться, но зато возникнет все возрастающая энергия магнитного поля , обусловленного током, текущим через индуктивность.

Поскольку активное сопротивление контура равно нулю, полная энергия, слагающаяся из энергий электрического и магнитного полей, не расходуется на нагревание проводов и будет оставаться постоянной. Поэтому в момент, когда напряжение на конденсаторе, а следовательно, и энергия электрического поля обращаются в нуль, энергия магнитного поля, а значит, и ток достигают наибольшего значения (стадия 2; начиная с этого момента ток течет за счет ЭДС самоиндукции). В дальнейшем ток уменьшается, и, когда заряды на обкладках достигнут первоначального значения , сила тока станет равной нулю (стадия 3). Затем те же процессы протекают в обратном направлении (стадии 4 и 5), после чего система приходит в исходное состояние (стадия 5) и весь цикл повторяется снова и снова. В ходе процесса периодически изменяются (т. е. колеблются) заряд на обкладках, напряжение на конденсаторе и сила тока, текущего через индуктивность. Колебания сопровождаются взаимными превращениями энергий электрического и магнитного полей.

На рис. 1 колебаниям в контуре сопоставлены колебания пружинного маятника. Сообщению зарядов обкладкам конденсатора соответствует выведение маятника внешней силой из положения равновесия и сообщение ему первоначального отклонения . При этом возникает потенциальная энергия упругой деформации пружины, равная 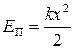. Стадии 2 соответствует прохождение маятника через положение равновесия. В этот момент квазиупругая сила равна нулю и маятник продолжает двигаться по инерции. К этому времени энергия маятника полностью переходит в кинетическую и определяется выражением и т.д. Аналогия между электрическими и механическими колебаниями распространяется и на описывающие их математи ческие уравнения.

Найдем уравнение колебаний в контуре без активного сопротивления. Условимся считать положительным ток, заряжающий конденсатор (рис.2).

Для цепи (рис.2) из обобщенного закона Ома для участка цепи следует

, (1)

где первое слагаемое – напряжение на конденсаторе, а второе ЭДС самоиндукции возникающая в катушке индуктивности. Используя определение силы тока , от уравнения (1) можно перейти к уравнению для заряда на конденсаторе:

. (2)

Если ввести обозначение уравнение (2) примет вид

. (3)

Последнее уравнение называется уравнением гармонического осциллятора, решением которого является функция

. (4)

Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой, определяемой выражением 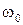, которая называется собственной частотой контура (она соответствует собственной частоте гармонического осциллятора).

Напряжение на конденсаторе отличается от заряда множителем :

. (5)

Продифференцировав функцию (4) по времени, получим выражение для силы тока

(6)

Таким образом, сила тока опережает по фазе напряжение на конденсаторе на . В момент, когда ток достигает наибольшего значения, заряд и напряжение обращаются в нуль и наоборот. Это соотношение между зарядом и током уже было установлено ранее, основываясь на энергетических соображениях.

Из формул (5) и (6) видно, что

(7)

3. Свободные затухающие колебания. Всякий реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего свободные колебания затухают. Для цепи (рис.3) из обобщенного закона Ома следует

(8)

Разделив это уравнение на и воспользовавшись определением силы тока получим

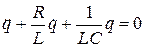. (9)

Введя обозначение , уравнению (9) можно придать вид

. (10)

Последнее уравнение совпадает с дифференциальным уравнением затухающих механических колебаний, решение которого имеет вид

. (11)

где называется частотой затухающих колебаний.

Таким образом, частота затухающих колебаний меньше собственной частоты 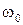. При выражение (11) переходит в (4).

Аналогично предыдущему разделу можно получить зависимости от времени напряжения на конденсаторе и силы тока в цепи.

График функции (11) изображен на рис.4. Графики для напряжения и силы тока имеют аналогичный вид. Время , за которое амплитуда заряда уменьшается в раз называется временем релаксации.

Затухание колебаний принято характеризовать логарифмическим декрементом затухания

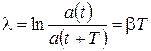(12)

Здесь – амплитуда соответствующей величины ( , или ). Логарифмический декремент затухания обратен числу колебаний , совершаемых за время, в течение которого амплитуда уменьшается в раз:

. (13)

Колебательный контур часто характеризуют его добротностью , которая определяется как величина, обратно пропорциональная логарифмическому декременту затухания:

. (14)

Можно показать, что при слабом затухании добротность механической колебательной системы с точностью до множителя равна отношению энергии, запасенной в системе в данный момент, к убыли этой энергии за один период колебаний.

(15)

В заключение отметим, что при , т.е. при вместо колебаний происходит апериодический разряд конденсатора (рис.5). Сопротивление контура 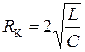, при котором колебательный процесс переходит в апериодический, называется критическим.

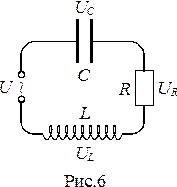4. Вынужденные электрические колебания. Резонанс напряжений. Чтобы вызвать вынужденные колебания, нужно оказывать на систему внешнее периодически изменяющееся воздействие. В случае электрических колебаний это можно осуществить, если включить последовательно с элементами контура переменную ЭДС или, разорвав контур, подать на образовавшиеся контакты переменное напряжение (рис.6). Для этой цепи из обобщенного закона Ома следует

(16)

Произведя преобразование, получим уравнение

. (17)

Уравнение (17) совпадает с дифференциальным уравнением вынужденных механических колебаний. Частное решение этого уравнения имеет вид

, (18)

где , (19)

. (20)

Общее решение получится, если к частному решению (18) прибавить общее решение соответствующего однородного уравнения. Это решение было получено в предыдущем параграфе (см. формулу (11)); оно содержит экспоненциальный множитель , поэтому по прошествии достаточного времени становится очень малым, и им можно пренебречь. Следовательно, установившиеся вынужденные колебания описываются функцией (18).

Продифференцировав выражение (18) по 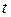, найдем силу тока в контуре при установившихся колебаниях:

(21)

где есть сдвиг по фазе между током и приложенным напряжением. При этом

, (22)

(23)

Представим уравнение (16) в виде

, (24)

или

(25)

Таким образом, сумма напряжений на отдельных элементах контура равна в каждый момент времени напряжению, приложенному извне (см. рис.6).

В соответствии с (24)

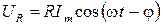. (26)

Разделив выражение (18) на емкость, получим напряжении е на конденсаторе

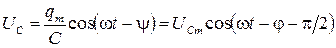, (27)

здесь .

Умножив производную функцию (21) на , получим напряжение на индуктивности:

, (28)

здесь .

Сопоставление формул (26), (27) и (28) показывает, что напряжение на емкости отстает по фазе от силы тока на (конденсатор не может зарядится мгновенно), а напряжение на индуктивности, в следствии явления самоиндукции, опережает ток, текущий в катушке, на .

Напряжение на активном сопротивлении изменяется в фазе с током. Фазовые соотношения можно представить очень наглядно с помощью векторной диаграммы. Напомним, что гармоническое колебание (или гармоническую функцию) можно задать с помощью вектора, длина которого равна амплитуде колебания, а направление вектора образует с некоторой осью угол, равный начальной фазе колебания. Возьмем в качестве прямой, от которой отсчитывается начальная фаза, ось токов. Тогда получается диаграмма, изображенная на рис.7 ( ).

Согласно (25) три функции , и в сумме должны быть равны приложенному напряжению . В соответствии с этим напряжение изображается на диаграмме вектором, равным сумме векторов , и .

Резонансная частота для заряда и напряжения на конденсаторе равна

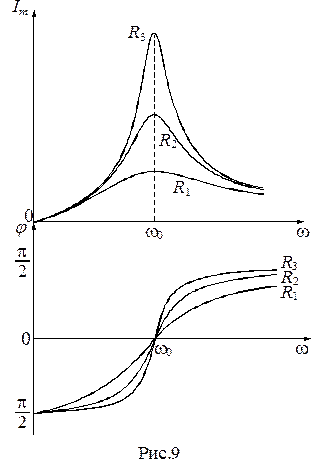
(29)

Резонансные кривые для изображены на рис.8 (резонансные кривые для имеют такой же вид). При резонансные кривые сходятся в одной точке с ординатой , что соответствует напряжению, возникающему на конденсаторе при подключении его к источнику постоянного напряжения.

Резонансные кривые и фаза для силы тока изображены на рис.9 ( ). Амплитуда силы тока имеет максимальное значение при . Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура :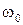

. (30)

Отрезок, отсекаемый резонансными кривыми на оси , равен нулю – при постоянном напряжении установившийся ток в цепи с конденсатором течь не может.

При малом затухании ( ) отношение амплитуды напряжения на конденсаторе при резонансе к амплитуде внешнего напряжения будет равно

. (31)

Таким образом, добротность показывает, во сколько раз напряжение на конденсаторе может превысить приложенное напряжение.

Остроту резонансных кривых определяет также добротность контура. На рис.10 показана одна из резонансных кривых для силы тока в контуре. По вертикальной оси отложены не значения , соответствующие данной частоте, а отношения к . Рассмотрим ширину кривой , взятую на высоте 0,7 (отношению амплитуд токов, равному 0,7, соответствует отношение мощностей, равное ~ 0,5). Можно показать, что отношение этой ширины к резонансной частоте равно величине, обратной добротности :контура:

(32)

Напомним, что формулы (31) и (32) верны лишь при больших значениях , т. е. в случае, когда затухание свободных колебаний в контуре мало.

Явление резонанса используется для выделения из сложного напряжения нужной составляющей. Пусть напряжение, приложенное к контуру, равно

Настроив контур на одну из частот , и т. д. (т. е. подобрав соответствующим образом его параметры и ), можно получить на конденсаторе напряжение, в раз превышающее значение данной составляющей, в то время как напряжение, создаваемое на конденсаторе другими составляющими, будет слабым. Таким образом, резонанс – явление резкого возрастания напряжения при совпадении частоты 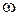внешнего переменного напряжения с собственной частотой 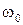контура. Такой процесс осуществляется, например, при настройке радиоприемника на нужную длину волны.

5. Переменный ток. Резонанс тока. Описанные в предыдущем параграфе установившиеся вынужденные колебания можно рассматривать как протекание в цепи, обладающей емкостью, индуктивностью и активным сопротивлением, переменного тока, обусловленного переменным напряжением . Этот ток изменяется по закону согласно формулам (21)-(23). Стоящее в знаменателе формулы (23) выражение

(33)

называется полным электрическим сопротивлением цепи или импедансом.

Всякая реальная цепь обладает конечными , и . В отдельных случаях некоторые из этих параметров бывают таковы, что их влиянием на ток можно пренебречь. Допустим, что цепи можно положить равным нулю, а – равным бесконечности. Тогда из формул (22) и (23) следует, что

, (34)

a ( ). Величину

(35)

называют реактивным индуктивным сопротивлением цепи или просто индуктивным сопротивлением цепи. Если выразить в Генри, а 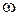– в обратных секундах ( ), то будет выражено в Омах. Из (35) следует, что индуктивное сопротивление растет с частотой 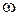. Постоянному току ( ) индуктивность не оказывает сопротивления. Ток индуктивности отстает от напряжения на индуктивности на .

Теперь допустим, что можно положить равными нулю и . Тогда согласно формулам (22) и (23)

, (36)

a ( ). Величину

(37)

называют реактивным емкостным сопротивлением или просто емкостным сопротивлением. Если выразить в Фарадах, а 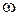– в обратных секундах ( ), то будет выражено в Омах. Из (37) следует, что емкостное сопротивление убывает с частотой. Для постоянного тока ; следовательно, постоянный ток через конденсатор течь не может. Поскольку , ток, текущий через конденсатор, опережает напряжение на конденсаторе на .

Наконец, допустим, что можно положить . В этом случае формула (23) переходит в

(38)

Величина

(39)

называется реактивным сопротивлением или реактансом.

Резонанс тока наблюдается в электрической схеме изображенной на рис.11, которая состоит из генератора синусоидальных колебаний с амплитудой , сопротивления внешней цепи , и соединенных параллельно конденсатора емкости и катушки индуктивности (колебательный контур). Общий ток цепи разветвляется на ток в конденсаторе и ток в катушке . Причем ток опережает на напряжение на конденсаторе , а ток отстает на от напряжения на катушке . Наглядно это можно представить в виде векторной диаграммы показанной на рис.12. Токи и имеют противоположные фазы (разность фаз составляет 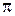) и в зависимости от их величины уравновешивают друг друга полностью или частично. Частота генератора, при которой в цепи имеет место резонанс тока, определяется из условия, что и общий ток цепи . Из вышесказанного следует , а .

Таким образом, резонансная частота при резонансе токов определяется собственной частотой колебательного контура 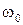. На рис.13 представлены зависимости амплитуды тока во внешней цепи в зависимости от частоты генератора для различных значений активного сопротивления ( ).

Полная проводимость при резонансе токов оказывается близкой к нулю. Остается некомпенсированной лишь небольшая активная проводимость, обусловленная активным сопротивлением катушки и несовершенной изоляцией конденсатора. Поэтому ток в неразветвленной цепи имеет минимальное значение, тогда как токи и могут превышать его в десятки раз.

6. Мощность тока. Найдем мощность, выделяемую в цепи переменного тока. Мгновенное значение мощности равно произведению мгновенных значений напряжения и силы тока:

(40)

Воспользовавшись тригонометрическими формулами выражению (40) можно придать вид 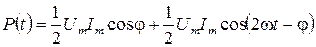. Практический интерес представляет среднее по времени значение , которое обозначим просто . В связи с тем, что среднее значение равно нулю,

. (41)

Из сказанного следует, что мгновенная мощность колеблется около среднего значения с частотой, в два раза превышающей частоту тока.

В соответствии с формулой (22) можем записать

. (42)

Подставив это значение в формулу (41), и учитывая, что , получим

(43)

Такую же мощность развивает постоянный ток, сила которого равна

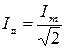(44)

Эта величина называется действующим (или эффективным) значением силы тока. Аналогично величина

(45)

называется действующим значением напряжения.

Выражение средней мощности через действующие значения сипы тока и напряжения имеет вид

. (46)

Входящий в это выражение множитель называют коэффициентом мощности. В технике стремятся сделать как можно большим. При малом для выделения в цепи необходимой мощности нужно пропускать ток большей силы, что при водит к возрастанию потерь в подводящих проводах.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Исследование вынужденных колебаний. Резонанс напряжений.

Подготовка к работе.

· Соберите цепь согласно схеме (рис.14).

· Подсоедините регулируемый источник синусоидального напряжения и установите на его входе напряжение частотой .

· В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой.

· Приведите компьютер в рабочее состояние и «подключите» виртуальные приборы , и .

· Частотомером измерите частоту колебаний и контролируйте ее в дальнейших исследованиях.

· выведите на дисплей виртуального осциллографа визуально форму вынужденных колебаний напряжения.

Порядок выполнения

· Изменяя частоту приложенного напряжения зафиксировать явление резонанса по максимальному значению тока.

· Изменяя частоту напряжения снимите зависимость эффективные значения , и . При этом по вольтметру поддерживайте постоянным напряжение на входе цепи. Интервал изменения частоты выбирать разным в зависимости от изменения измеряемой величины: в областях частот близких к резонансной – интервал частот необходимо уменьшать. Полученные результаты запишите в табл.1.

Таблица 1



…

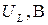
Обработка результатов измерений

· По результатам измерений постройте график зависимости тока от частоты . Сравните экспериментальную кривую с теоретической (рис.9).

· По результатам измерений построить график зависимости и от частоты . Сравнить полученные экспериментальные зависимости с теоретическими определяемыми по формулам (34) и (36).

· Из экспериментального графика при известном значении емкости конденсатора найти следующие параметры конура: – резонансную частоту, – добротность, – индуктивность катушки трансформатора, – сопротивление контура.

Резонанс токов.

Подготовка к работе.

· Соберите цепь согласно схеме (рис.15).

· Приведите компьютер в рабочее состояние и «подключите» виртуальные приборы , , и .

· Частотомером измерите частоту колебаний и контролируйте ее в дальнейших исследованиях.

· выведите на дисплей виртуального осциллографа визуально форму вынужденных колебаний напряжения.

Порядок выполнения

· Изменяя частоту приложенного напряжения зафиксировать явление резонанса по минимальному значению тока.

Таблица 2



…

Обработка результатов измерений

· По результатам измерений постройте график зависимости тока от частоты . Сравните экспериментальную кривую с теоретической (рис.13).

· Из экспериментального графика при известном значении емкости конденсатора найти следующие параметры конура: – резонансную частоту, – индуктивность катушки трансформатора, – сопротивление контура.

ЛИТЕРАТУРА

1. Савельев И.В. Курс общей физики. В 5 кн. Кн.2. Электричество и магнетизм. – М.: ООО “Издательство Астрель”: ООО “Издательство АСТ”, 2002.

2. Иродов И.Е. Электромагнетизм. Основные законы./И.Е. Иродов – 5.-е изд. – М.: БИНОМ. Лаборатория знаний, 2006.

3. Трофимова Т.И. Курс физики. М.: Высшая школа, 2003.

4. Детлаф А.А., Яворский Б.М. Курс физики. М.: Изд. центр “Академия”, 2003.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Колебательный контур без потерь. Свободные колебания.

2. Колебательный контур с потерями. Апериодический процесс.

3. Вынужденные колебания. Уравнение и его решение.

4. Резонанс напряжений. Понятие добротности контура.

5. Переменный ток. Векторные диаграммы.

6. Резонанс токов.

7. Методика эксперимента.