Главная | Обратная связь

ПРИМЕР К ЗадаЧЕ 1.2

 

Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стальным стержням при помощи шарниров.

Требуется:

1. Найти усилия и напряжения в стержнях, выразив их через силу Q.

2. Используя метод расчета по допускаемым напряжениям найти допускаемую нагрузку [Q].

3. Найти предельную грузоподъемность системы Q_т и допускаемую нагрузку [Q]_т путем расчета по предельному состоянию. Запас прочности к = 1.5.

4. Сравнить величины [Q] и [Q]_т .

Рис.1

a = 40 см, b = 20 см, с= 30 см А - площадь поперечного сечения стержня ВМ 2А- площадь поперечного сечения стержня СК А = 10 см2 , sт = 24 кН/см2 [s] = 16 кН/см2

 

РЕШЕНИЕ

1. Определяем необходимые геометрические параметры (длины стержней ВМ и СК, a - угол наклона стержня СК).

l₁=ВМ=40 см

l₂=СК= = = 56.569 см

sin a = DК / СК = 40 / 56.569= 0.707, cos a = СD/CK=0,707

2. Строим силовую схему (рис. 2). Указываем направление опорных реакций R_D и H_D, внутренних усилий в стержнях N₁ и N₂. Неизвестные усилия N₁ и N₂ считаем растягивающими.

Рис.2

3. Определяем степень статической неопределимости m = 4 - 3 = 1

Здесь 4 - число неизвестных ( R_D, H_D, N₁, N₂)

3 - число уравнений статики.

4. Записываем уравнения статики

S x = 0 H_D + N₂ cosa = 0;

S y = 0- N₁ - R_D + N₂ sina + Q= 0 ;

S M_D= 0 - N₁ 70 + N₂ 40 sin a - Q20 = 0.

В данной задаче не требуется отыскивать опорные реакции R_D и H_D, поэтому из трех уравнений статики используем одно:

S M_D= 0 - N₁ 70 + N₂ 40 sin a - Q 20 = 0 (1)

Из одного уравнения (1) невозможно определить два неизвестных усилия N₁ и N_2.

Задача один раз статически неопределима.

5. Составляем условие совместности деформаций.

Используя предположение о малости деформаций, строим деформированную схему конструкции (рис. 3). Абсолютно жесткий брус BL под действием приложенной нагрузки Q поворачивается на малый угол вокруг опоры (т.D), оставаясь прямолинейным. При этом первый стержень сжимается на величину Dl₁ ( т. В переходит в т. В₁ ), а второй стержень растягивается на величину Dl₂ (т.С переходит в С₁ ).

Рис. 3

 

Здесь ВВ₁ ^ BD, CC₁ ^ CD, D l₁ = BB₁, D l₂ = CC₂

Чтобы получить т. С₂ из т. С₁ опускаем перпендикуляр на первоначальное направление стержня СК.

Из подобия треугольников D BB₁D и D СС₁D следует:

или

Здесь CC₁ = Dl₂ / sin a из D CC₁C₂. Знак минус показывает, что первый стержень укорачивается. Итак получили условие совместности деформаций:

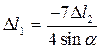или (2)

6. Используя закон Гука, из уравнений (1) и (2) определяем усилие и напряжения. Согласно закону Гука:

По условию задачи А₂ = 2 А₁

Подставляя в (2), получим N₁= -1,750 N₂ (3)

 

Решаем совместно систему уравнений (1), (3). Получаем:

- (-1.750 N₂ ) 70 + N₂ 40 0.707 - Q 20 =0. Откуда

N₂ = 0,133 Q ( растяжение )

N₁ = - 1,750 N₂ = - 0.233 Q ( сжатие )

Определяем напряжения в стержнях:

где A₁ =A =10 см² A₂ = 2 A = 20 см²

7. Определяем допускаемую нагрузку [Q].

Приравнивая максимальное напряжение по модулю |s₁| допускаемому [s], получаем допускаемую нагрузку [Q]:

|s₁ | = 0.0233 [Q] = 16 кН/см² Þ [Q] = 16 / 0.0233 = 689.655 кН.

 

8. Вычисляем предельную грузоподъемность Q_Т.

Считаем s₁ = s_T, s₂ =s_T. Тогда 240 кН, (сжатие)

кН/см², 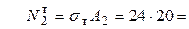480 кН.

Подставляя и в (1), с учетом истинного направления усилия (сжатия), находим предельное значение Q_Т:

Допускаемое значение [Q]_т по предельному состоянию

кН

9. Сравнивая величины [Q] = 689,655 кН и [Q]_T =1012.48 кН, видим, что расчет по предельному состоянию позволяет расширить диапазон допускаемых нагрузок

.