Главная | Обратная связь

Приклади лінійних просторів.

Лекція 6

 

 

Тема:" Лінійні простори. Аксіоматика. Приклади лінійних просторів. Лінійна залежність і незалежність. Лінійні многовиди. Базис. Вимірність простору. Ізоморфізм".

 

Дисципліна : "Функціональний аналіз".

 

 

Викладач Гусарова І.Г.

 

 

Харків,2013

 

Тема: Лінійні простори. Аксіоматика. Приклади лінійних просторів. Лінійна залежність і незалежність. Лінійні многовиди. Базис. Вимірність простору. Ізоморфізм

Лінійні простори. Приклади лінійних просторів.

Означення: Лінійним або векторним простором називається не порожня множина елементів довільної природи якщо вона задовольняє наступним умовами (аксіомами):

1). Для будь-яких двох елементів 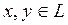однозначно визначений третій елемент ,який зветься сумою та позначається , причому

1. (комутативність);

2. (асоціативність);

3. 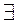нульовий елемент 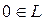: х+0=х, для ;

4. для всіх існує елемент – такий, що х+(-х)=0.

2). Для будь-якого числа і для будь-якого елемента 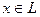визначений елемент 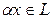(добуток елемента на число), причому

1. a(bх)=(ab)х;

2. ;

3. (a+b)х=aх+bх;

4. .

В залежності від того, на які числа допускається множення, на дійсні або комплексні, розрізняють дійсні або комплексні лінійні простори. Зауважимо, що всякий комплексний лінійний простір як деякий дійсний лінійний простір, якщо обмежитися в ньому множенням векторів на дійсні числа.

 

Приклади лінійних просторів.

1). Пряма лінія ,тобто сукупність дійсних чисел з звичайними арифметичними операціями додавання і множення представляє з себе лінійний простір.

2). 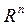- дійсний, - вимірний арифметичний простір є лінійним простором. Він визначається як сукупність впорядкованих наборів 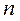дійсних чисел , де додавання і множення визначаються формулами

(1)

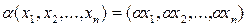. (2)

3). - комплексний 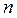- вимірний арифметичний простір 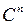. Він визначається як сукупність впорядкованих наборів комплексних чисел де додавання і множення визначаються формулами (1),(2) з множенням на будь - які комплексні числа.

4). Неперервні (дійсні або комплексні) функції на деякому відрізку [а, b] із звичайними операціями складання функцій і множення їх на числа утворюють лінійний простір .

5). Простір 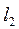, де елементи - послідовності чисел (дійсних або комплексних), 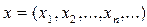які задовольняють умові

(3) з операціями

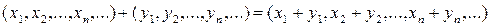(4)

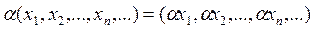, (5)

є лінійним простором. Той факт, що сума двох послідовностей, що задовольняють умові (3), також задовольняє цій умові, слідує з елементарної нерівності

.

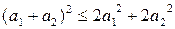5). Збіжні послідовності 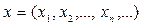із по координатними операціями додавання і множення на числа (4),(5) утворюють лінійний простір .

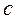6). Послідовності, які збіжні до 0, із по координатними операціями додавання і множення на числа (4),(5) утворюють лінійний простір .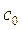

7). Сукупність всіх обмежених послідовностей, із по координатними операціями додавання і множення на числа (4),(5) є лінійним простором.

8). Сукупність всіляких числових послідовностей, із по координатними операціями додавання і множення на числа (4),(5) є лінійним простором.

 

Ізоморфізм.

Властивості лінійного простору визначаються властивостями операцій додавання елементів і множення їх на числа, тому вводиться наступне означення.

Означення:Лінійні простори 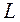і 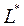називаються ізоморфними, якщо між їх елементами можна встановити взаємно однозначну відповідність, яка узгоджена з операціями в 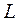і . Це означає, що з

, ( , )

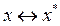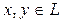слідує , 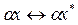( - довільне число).

Ізоморфні простори можна розглядати як різні реалізації одного й того же простору.

 

Приклад. Простір ( 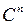) і простір всіх многочлени степені 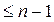з дійсними (або комплексними) коефіцієнтами зі звичайними операціями додавання і множення на числа ізоморфні.