 |
|
Модель Кронига – Пенни.
Для нахождения энергетического спектра электронов в кристалле необходимо решить одноэлектронное уравнение Шредингера с периодическим потенциалом решетки V(r).Собственные функции 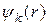 и собственные значения
и собственные значения  этого уравнения зависят от вида периодического потенциала. В тоже время точный вид V(r) определить практически невозможно. В этих условиях для нахождения решения уравнения Шредингера приходится применять различные предположения относительно вида функции V(r).
этого уравнения зависят от вида периодического потенциала. В тоже время точный вид V(r) определить практически невозможно. В этих условиях для нахождения решения уравнения Шредингера приходится применять различные предположения относительно вида функции V(r).
Следуя Кронигу и Пенни, рассмотрим простую одномерную модель. В этой модели зависимость потенциальной энергии электрона от расстояния х для одномерной решетки можно представить следующим образом:

Рис. 1.44. Модель Кронига-Пенни с периодическим потенциалом прямоугольной формы.
а – ширина области с V = 0, b – ширина области c V = V0.
Здесь прямоугольные потенциальные ямы шириной a (I) чередуются с прямоугольными барьерами шириной b (II). Период такой решетки c=a+b.
Таким образом, потенциальная энергия представляет собой функцию: 
V (x)=0 nc<x<nc+a V(x)=V0 nc+a<x<(n+1)c
Здесь n – любое число (0,  )
)
Запишем одноэлектронное уравнение Шредингера для одномерного случая
 (1.56)
(1.56)
Решение этого уравнения будем искать в виде функции Блоха
 (1.57)
(1.57)
где U(x) – некая периодическая функция с периодом решетки, т.е.
U(x)=U(x+c)=U(x+2c)=… (1.58)
Найдем уравнение, которому должна удовлетворять функция U(x). Подставив (1.57) в (1.56) получим для области  , а также для любой другой потенциальной ямы:
, а также для любой другой потенциальной ямы:

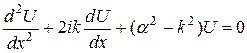 (1.59)
(1.59)
и для области 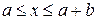 , а также любого другого потенциального барьера:
, а также любого другого потенциального барьера:
 (1.60)
(1.60)
где  и
и  (1.61)
(1.61)
Решение уравнения (1.59) и (1.60) имеют вид
 (1.62)
(1.62)
Последние выражения содержат четыре неизвестных A,B,C и D, которые находят из условия непрерывности волновой функции и ее первых производных, а также с учетом периодичности потенциального рельефа решетки.
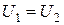 при x=n(a+b)
при x=n(a+b)
 при x=a+n(a+b) (1.63)
при x=a+n(a+b) (1.63)
Подставляя (1.63) в (1.62) и решая систему уравнений нетрудно убедится, что условие существования решения системы задается уравнением:
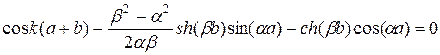 (1.64)
(1.64)
Уравнение (1.64) связывает величины  и
и  , содержащие собственные значения энергии электрона Е, с волновым вектором
, содержащие собственные значения энергии электрона Е, с волновым вектором  . Таким образом, равенство (1.64) можно рассматривать как соотношение между Е и К.
. Таким образом, равенство (1.64) можно рассматривать как соотношение между Е и К.
Решить уравнение (1.64) очень сложно. Поэтому вводят дополнительно упрощающие предположения.
Пусть  , а
, а 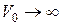 , но так, чтобы произведение ширины барьера на высоту в V0 оставалось конечным причем
, но так, чтобы произведение ширины барьера на высоту в V0 оставалось конечным причем  - конечно,
- конечно, 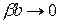 , (т.е. мы рассматриваем тонкие высокие барьеры). При
, (т.е. мы рассматриваем тонкие высокие барьеры). При  ,
,  ,
,  ,
, 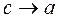 и , наконец, cosk(a+b) à cos ka
и , наконец, cosk(a+b) à cos ka
С учетом этого, вместо (1.64) можно записать
 (1.65)
(1.65)
А также учтем, что 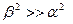 ,
,
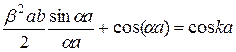 (1.66)
(1.66)
Обозначим 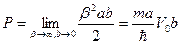 (1.67)
(1.67)
Величина Р представляет собой меру эффективной площади каждого барьера. Он характеризует степень прозрачности барьера для электрона или, другими словами степень связанности электрона в потенциальной яме. С учетом этого можно записать уравнение Кронига-Пенни в следующем (окончательном) виде:

 , где: (1.68)
, где: (1.68)
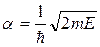 и
и 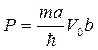
В правой части уравнения (1.68) стоит функция cos ka. Она четная. Замена k на (-k) не меняет уравнение (1.68). Это означает, что энергия электрона также является четной функцией волнового вектора k, то есть
Е(-k)=Е(k) (1.69)
Решить уравнение Кронига-Пенни (1.68) можно графически. Зависимость левой части уравнения от параметра 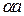 можно изобразить таким образом
можно изобразить таким образом

Рис.1.45.Разрешенные (заштрихованные) и запрещенные (светлые) зоны для Кронига – Пенни.
Поскольку cos ka - в правой части уравнения - может принимать только значения от –1 до +1, то допустимыми значениями 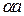 являются такие, для которых левая часть уравнения не выходит из указанных пределов.. На рис.1.45 интервалы разрешенных значений
являются такие, для которых левая часть уравнения не выходит из указанных пределов.. На рис.1.45 интервалы разрешенных значений 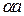 заштрихованы. Ширина этих интервалов зависит от параметра Р. Чем меньше Р, тем они шире (физическая интерпретация!). Кроме того, их ширина зависит и от
заштрихованы. Ширина этих интервалов зависит от параметра Р. Чем меньше Р, тем они шире (физическая интерпретация!). Кроме того, их ширина зависит и от 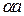 . При любом фиксированном значении Р эти интервалы расширяются с увеличением
. При любом фиксированном значении Р эти интервалы расширяются с увеличением 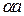 .
.
Таким образом, учитывая связь a с Е, можно заключить, что энергия электрона в кристалле не может принимать любого значения. Есть зоны разрешенных и запрещенных энергий, которые можно изобразить так, как показано на рис.
Рассмотрим как изменяется спектр в двух предельных случаях: Р 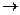 0 и
0 и
Р 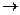
 .
.
Первый случай (Р 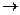 0) соответствует условию V0
0) соответствует условию V0 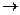 0, то есть почти свободному электрону (приближение слабой связи).
0, то есть почти свободному электрону (приближение слабой связи).
Из соотношения (1.68) следует, что a=k. С учетом формулы (2.13) можем записать:
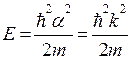
Последнее выражение совпадает с зависимостью Е (к) для свободного электрона (1.28).
Второй предельный случай (Р 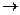
 в силу того что V0
в силу того что V0  0) соответствует локализации электрона в бесконечно глубокой яме, то есть электрон очень сильно связан. {Физический эквивалент – электрон находится в потенциальной яме с непроницаемыми стенками или внутри квантовой точки}. При Р
0) соответствует локализации электрона в бесконечно глубокой яме, то есть электрон очень сильно связан. {Физический эквивалент – электрон находится в потенциальной яме с непроницаемыми стенками или внутри квантовой точки}. При Р 
 из уравнения (1.68) находим:
из уравнения (1.68) находим:
 sin(
sin( 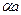 )/(
)/( 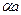 )=0
)=0
то есть
aa = 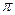 n где n=
n где n=  1;
1;  2;
2;  3;…..
3;…..
Тогда:
 , что совпадает с формулой (1.29)
, что совпадает с формулой (1.29)
 Таким образом, при Р
Таким образом, при Р 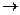
 система энергетических зон вырождается в дискретные уровни (в прямоугольном потенциальном ящике).
система энергетических зон вырождается в дискретные уровни (в прямоугольном потенциальном ящике).
Промежуточный случай – сильная связь электрона с атомами кристаллической решетки.Для электрона, движущегося в периодическом поле решетки, явный вид закона дисперсии Е(к) можно найти, решив уравнение (1.68). Это можно сделать, допустив, что Р>>1. Такое предположение соответствует случаю сильной связи. В приближении сильной связи выражение для энергии электрона в кристалле имеет вид:
E(k)=Eon-Cn+(-1)nAncoska (1.70)
где  - энергия n–го энергетического уровня электрона в изолированной бесконечно глубокой яме (рис. 1.46а). Величина
- энергия n–го энергетического уровня электрона в изолированной бесконечно глубокой яме (рис. 1.46а). Величина 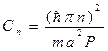 - мала, поскольку P>>1. Сn идет со знаком минус, поэтому соответствующие энергетические уровни E0n на рис. 1.46а несколько снижаются.
- мала, поскольку P>>1. Сn идет со знаком минус, поэтому соответствующие энергетические уровни E0n на рис. 1.46а несколько снижаются.
An - коэффициент, в общем случае не равный Сn. An определяет амплитуду косинусоидальной зависимости E(k) (рис. 1.46 б)
Второй и третий члены отражают действие периодического поля решетки. Видно, что в периодическом поле решетки энергетические уровни опускаются на значение Сn (перед Сn стоит знак минус). Это свидетельствует о том, что объединение атомов в цепочку выгодно. Третий член определяет в (1.70) зонный характер энергетического спектра. Таким образом, зависимость E(k) может быть изображена, как на рис.1.46 б.

| 
|
Рис.1.46. Построение периодической зонной схемы (б) в приближении сильной связи в соответствии с формулой 1.70.
Зависимость Е(k) для электрона, находящегося в кристаллической решетке имеет вид: 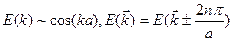 , поэтому для всех k, отличающихся на величину (2n
, поэтому для всех k, отличающихся на величину (2n 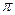 /a), энергия одна и та же. Т.е. энергия электрона является периодической функцией волнового вектора. Интервал значений от -
/a), энергия одна и та же. Т.е. энергия электрона является периодической функцией волнового вектора. Интервал значений от - 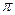 /a до
/a до 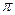 /a представляет первую зону Бриллюэна. Два отрезка от - 2
/a представляет первую зону Бриллюэна. Два отрезка от - 2 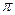 /a до -
/a до - 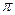 /a и от
/a и от 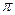 /a до 2
/a до 2 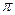 /a вторую зону Бриллюэна и так далее. Поскольку и волновая функция электрона и энергия электрона в кристалле являются периодическими функциями, поэтому периодическую зонную схему можно свести в первую зону Бриллюэна.
/a вторую зону Бриллюэна и так далее. Поскольку и волновая функция электрона и энергия электрона в кристалле являются периодическими функциями, поэтому периодическую зонную схему можно свести в первую зону Бриллюэна.
Повторение-напоминание (еще раз):
Волновая функция Блоха – периодична, поэтому  . Это трансляционное условие выполняется и для вектора . Это трансляционное условие выполняется и для вектора  (где (где  - вектор обратной решетки). Следовательно, состояния, характеризующиеся волновым вектором - вектор обратной решетки). Следовательно, состояния, характеризующиеся волновым вектором  и и 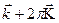 физически эквивалентны. Т. е. энергия электронов находящихся в этих двух состояниях одинакова. Другими словами: и волновая функция и энергия электронов, находящихся в кристалле является периодическими функциями волнового вектора физически эквивалентны. Т. е. энергия электронов находящихся в этих двух состояниях одинакова. Другими словами: и волновая функция и энергия электронов, находящихся в кристалле является периодическими функциями волнового вектора  с периодом с периодом 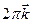 : :  Если в
Если в  -пространстве (или в -пространстве (или в 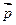 -пространстве ) построить обратные решетки с векторами -пространстве ) построить обратные решетки с векторами 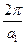 ; ;  ; ;  или или  ; ;  ; ;  ; то все ; то все  -пространство можно разделить на области, в которых имеются физически эквивалентные состояния. Эти области называются зонами Бриллюэна. -пространство можно разделить на области, в которых имеются физически эквивалентные состояния. Эти области называются зонами Бриллюэна.
|
Зависимость Е(k) часто строят только для первой зоны Бриллюэна (рис. 1.47а). Такой способ изображения Е(k) получил название схемы приведенных зон, в отличие от первого, называемого периодической зонной схемой (1.46б).

|

| ||||
| Рис. 1.47. (а) - схема приведенных зон, (б) – расширенная зонная схема. |
Кроме этих двух способов используют еще один, получивший название расширенной зонной схемы. Здесь различные энергетические зоны размещаются в k-пространстве в различных зонах. Разрывы в энергетическом спектре электрона, как видно из рисунка, появляются на границах зон Бриллюэна (±1/2G, ±G и т.д.):
 , где 2UG =Eg - запрещенная зона
, где 2UG =Eg - запрещенная зона
Зонная структура в трехмерном случае может быть сложнее, чем в рассматриваемой одномерной модели. Как правило, зависимость Е(k) в трехмерном кристалле различна для разных направлений в зоне Бриллюэна. Это связано с тем, что трехмерный потенциал V(r), зависящий от структуры кристалла, в различных направлениях не одинаков. Следствием этого может быть перекрытие разрешенных зон, или запрещенная зона в одном направлении может совпадать с разрешенной зоной в другом направлении.
1.3.4. Эффективная масса носителей заряда
На свободный электрон, помещенный в однородное электрическое поле E, действует сила F=-qE, под действием которой электрон приобретает ускорение  . Здесь т — масса электрона. Поскольку
. Здесь т — масса электрона. Поскольку  является единственной силой, определяющей характер движения частицы, вектор ускорения электрона направлен так же, как и вектор внешней силы, т.е. против поля E.
является единственной силой, определяющей характер движения частицы, вектор ускорения электрона направлен так же, как и вектор внешней силы, т.е. против поля E.
В кристалле, внешнее поле E действует на электрон так же, как на свободный электрон: с силой F=-qE, направленной против поля. Однако, кроме силы -qE, на электрон действуют значительные внутренние силы, создаваемые периодическим полем решетки. Это означает, что ускорение электрона в решетке в общем случае может быть не направлено параллельно внешней силе  . Следовательно, движение электрона в кристалле будет более сложным, чем движение свободного электрона. Именно поэтому энергия электрона, движущегося в периодическом поле кристалла, не имеет квадратичной зависимости от волнового вектора E ≠ p2/2m. Это также следует из теоретических моделей (например, модели Кронига и Пенни). Однако для практических целей иногда удобно сохранить зависимость энергии электрона от квазиимпульса в классическом виде, а все различия, вызванные влиянием периодического поля, включить в массу электрона. Тогда формулу Е
. Следовательно, движение электрона в кристалле будет более сложным, чем движение свободного электрона. Именно поэтому энергия электрона, движущегося в периодическом поле кристалла, не имеет квадратичной зависимости от волнового вектора E ≠ p2/2m. Это также следует из теоретических моделей (например, модели Кронига и Пенни). Однако для практических целей иногда удобно сохранить зависимость энергии электрона от квазиимпульса в классическом виде, а все различия, вызванные влиянием периодического поля, включить в массу электрона. Тогда формулу Е  р2/2m можно переписать в виде Е=р2/2m*, где вместо т появляется некоторая величина т*, которая является функция энергии, и которая называемая эффективной массой. Для определения понятия эффективной массы можно воспользоваться несколькими подходами.
р2/2m можно переписать в виде Е=р2/2m*, где вместо т появляется некоторая величина т*, которая является функция энергии, и которая называемая эффективной массой. Для определения понятия эффективной массы можно воспользоваться несколькими подходами.
(а) Определение эффективной массы из разложения в ряд Тейлора (формальный, математический метод). В одномерном случае величину т* можно рассчитать из разложения энергии в ряд Тейлора около экстремальных точек (т. к. E(k)- периодическая функция k и E(k)~cos(k) (периодический член))
 (1.71)
(1.71)
Так как в точках k=ko энергия имеет максимум или минимум (см. рис. 1.46, 1.47), то первая производная равна нулю. Ограничиваясь вторым приближением, из (1.71) находим:
 (1.72)
(1.72)
Или:  (1.73)
(1.73)
Если E(k)-E(k0)=E(k1), а k-k0=k1, тогда  ,
,
Следовательно, роль эффективной массы играет величина
 (1.74)
(1.74)
В низших точках разрешенных зон Е(k) имеет минимумы, а вторая производная от Е по k больше нуля. Поэтому на дне зоны эффективная масса положительна, а в вершинах зон отрицательна, поскольку d2E/ dk2<0. В некоторой точке в центре зоны m* ®  . Очевидно, разложение энергии в степенной ряд (1.71) и формула (1.74) справедливы только вблизи точек экстремума.
. Очевидно, разложение энергии в степенной ряд (1.71) и формула (1.74) справедливы только вблизи точек экстремума.
(б) Определение эффективной массы из квазиклассического подхода.
Понятие эффективной массы имеет более широкие границы применимости и может быть введено исходя из принципа соответствия. Известно, что средние квантовомеханические величины удовлетворяют тем же соотношениям, что и соответствующие им классические величины. Так, волновые пакеты, составленные из решений уравнения Шредингера, движутся по траекториям классических частиц. Поэтому уравнению Ньютона должен соответствовать квантовомеханический аналог, то есть квантовомеханическое уравнение движения электрона в кристалле.
Таким образом, можно использовать квазиклассический подход (наполовину классический, наполовину квантовомеханический). В этом подходе квантовомеханическим, является определение электрона как волны. В этом случае движение электрона в кристалле можно описать с помощью волнового пакета, составленного из блоховских функций. Тогда средняя скорость движения электрона равна групповой скорости распространения всего волнового пакета -  . Учитывая, что
. Учитывая, что 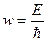 , для групповой скорости получаем:
, для групповой скорости получаем:
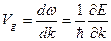 (1.75)
(1.75)
Аналогичным образом можно ввести усредненное ускорение волнового пакета (электрона) в кристалле:
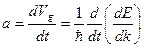 (1.76)
(1.76)
С учетом того, что время и квазиимпульс независимы, в (1.76) можно поменять местами порядок их дифференцирования:
 (1.77)
(1.77)
Классическим,в настоящем подходе,является определение работы внешней силы над рассматриваемым электроном, которая приводит к увеличению энергии (скорости) электрона:
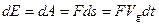 , откуда
, откуда 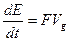 или
или  (1.78)
(1.78)
Подставляя (1.78) в (1.77) и учитывая, что внешняя сила F не зависит от k, получим:
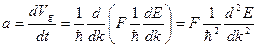 (1.79)
(1.79)
Перепишем в виде: 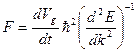 (1.80)
(1.80)
Т.е. по аналогии с законом Ньютона, величину 
 можно назвать массой электрона:
можно назвать массой электрона:
 (1.81)
(1.81)
Величина т* получила название эффективной массы электрона. Эффективная масса отражает влияние периодического потенциала решетки на движение электрона в кристалле под действием внешней силы. В периодическом поле кристаллической решетки электрон движется под действием внешней силы F в среднем так, как двигался бы свободный электрон под действием этой силы, если бы он обладал массой т* Таким образом, если электрону в кристалле вместо массы т приписать эффективную массу т*, то его можно считать свободным и движение этого электрона описывать так, как описывается движение свободного электрона, помещенного во внешнее поле. Разница между т* и m обусловлена взаимодействием электрона с периодическим полем решетки, и, приписывая электрону эффективную массу, мы учитываем это взаимодействие.
| Эффективная масса, в отличие от обычной массы, не определяет ни инерционных, ни гравитационных свойств частицы. Она является лишь коэффициентом в уравнении движения и отражает меру взаимодействия электрона с кристаллической решеткой. |
Пользуясь понятием эффективной массы, задачу о движении электрона в периодическом поле решетки V( 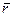 ) можно свести к задаче о движении свободного электрона с массой т*. Это значит, что вместо уравнения Шредингера с периодическим потенциалом
) можно свести к задаче о движении свободного электрона с массой т*. Это значит, что вместо уравнения Шредингера с периодическим потенциалом
 , нужно решать уравнение
, нужно решать уравнение
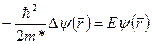 , (1.82)
, (1.82)
Метод решения уравнения Шредингера, в котором вид периодического потенциала решетки автоматически учитывается через эффективную массу, называется методом эффективной массы
В общем случае эффективная масса является анизотропной величиной и для разных направлений волнового вектора  различна. Она представляет собой тензор второго ранга:
различна. Она представляет собой тензор второго ранга:
 или
или  (1.83)
(1.83)
Таким образом, если зависимость 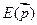 [закон дисперсии] анизотропна, то эффективная масса представляет собой тензор обратных эффективных масс.
[закон дисперсии] анизотропна, то эффективная масса представляет собой тензор обратных эффективных масс.
Рассмотрим некоторые свойства эффективной массы.
Из формул (1.74), (1.81), (1.85) следует, что эффективная масса определяется видом дисперсионной зависимости E(k). В приближении сильной связи выражение E(k) имеет вид (1.70), как это следует из модели Кронига-Пенни. Периодичность волновой функции (1.51), (1.52) и энергии электрона в кристалле (1.54) позволяет ограничиться рассмотрением зависимости E(k) в первой зоне Бриллюэна. Возьмем первую (нижнюю) ветку дисперсионной кривой E(k) в первой зоне Брилюэна для кристалла кубической сингонии (рис. 1.48а) и проведем дифференцирование. Поскольку E(k) имеет функциональную зависимость, близкую к E(k) ~ cos (ka) (см. формулу (1.70)), первая производная вблизи точек экстремума будет близкой к зависимости dE/dk ~ sin (ka). Во всей первой зоне Бриллюэна, зависимость dE/dk есть зависимость скорости электрона от волнового вектора k: (dE/dk=Vg).
Вторая производная и ее обратная зависимость (пропорциональная эффективной массе) приведены на рис. 1.48. Сравнение зависимости E(k) на рис. 1.48(а) и зависимости m*(k) на рис. 1.48(г) позволяет сделать следующие комментарии. Электрон, находящийся внутри идеальной периодической решетки может иметь как положительную, так и отрицательную эффективную массу. Если кривая на диаграмме E-k имеет выпуклость вниз (относительно оси энергий, если принять направление увеличения энергии - вверх), то масса m*>0. Если же кривая имеет выпуклость вверх (около  ), тогда m*<0.
), тогда m*<0.
Отрицательная эффективная масса означает, что ускорение электрона направлено против действия внешней силы. Это видно из рис. 1.48б. При k, близких к границе зоны Бриллюэна, несмотря на увеличение k, скорость электрона уменьшается. Данный результат является следствием брэгговского отражения. В точке k= 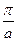 — состояние электрона описывается уже не бегущей, а стоячей волной и
— состояние электрона описывается уже не бегущей, а стоячей волной и  =0. В случае, когда m*<0 (на рис. 1.48(г) это области –π/a<k<π/2a и π/2a<k<π/a), частица будет ускоряться в направлении, противоположном направлению движения нормального (отрицательно заряженного) электрона; т.е. будет вести себя как некоторая гипотетическая частица, с положительным зарядом и положительной массой. Поскольку свойства электронов с отрицательной эффективной массой очень сильно отличаются от свойств "нормальных" электронов, их удобнее описывать, пользуясь представлением о некоторых квазичастицах, имеющих заряд +е, но и положительную эффективную массу. Такая, квазичастица[1] получила название дырка. Обозначение дырки – h (от англ. «hole»).
=0. В случае, когда m*<0 (на рис. 1.48(г) это области –π/a<k<π/2a и π/2a<k<π/a), частица будет ускоряться в направлении, противоположном направлению движения нормального (отрицательно заряженного) электрона; т.е. будет вести себя как некоторая гипотетическая частица, с положительным зарядом и положительной массой. Поскольку свойства электронов с отрицательной эффективной массой очень сильно отличаются от свойств "нормальных" электронов, их удобнее описывать, пользуясь представлением о некоторых квазичастицах, имеющих заряд +е, но и положительную эффективную массу. Такая, квазичастица[1] получила название дырка. Обозначение дырки – h (от англ. «hole»).

|
 
| ||
| Рис. 1.48. Зависимость энергии (а), скорости (которая ~ dE/dk) (б), величины d2E/dk2 (в) и эффективной массы (г) от волнового вектора для кубической решетки. | Рис. 1.49. Схема перемещения связанных носителей (электронов) и свободных носителей (дырок) внутри валентной зоны. |
Понятие дырки поясним следующим примером (рис. 1.49):
Предположим, в исходном состоянии валентная зона полностью заполнена электронами (нет свободных энергетических уровней), а зона проводимости – свободна. Включив внешний приток энергии (нагрев, облучение светом, радиацией и др.), можно инициировать переход электронов из валентной зоны в зону проводимости. Предположим далее, что энергия фотона передаётся электрону в валентной зоне и он переходит в зону проводимости (процесс А на рис. 1.49). С точки зрения химической связи это означает повреждение (разрыв) ковалентной связи и уход электрона в свободное перемещение по кристаллу. С точки зрения зонной теории, электрон уходит в зону проводимости, а на потолке валентной зоны образуется незанятое место (квантовое состояние).
Если внешнее электрическое поле E равно нулю и вследствие того, что электроны стремятся занять самые нижние энергетические состояния, дырка занимает самое верхнее состояние (позицию 1 на рис. 1.49). Под действием электрического поля E на это незанятое состояние перейдет электрон с более низкого энергетического уровня: на рис. 1.49 это обозначено переходом электрона из позиции 2 в позицию 1. Дырка при этом опустится из позиции 1 в позицию 2. Затем этот процесс может повториться переходом (3 à 2) и т.д. по эстафете. При таком перемещении электронов, освобождающееся незанятое место на энергетическом уровне перемещается вниз, вглубь валентной зоны. Этот освобождающийся уровень и отождествляется с некоей фиктивной частицей, которая имеет равный по значению, но противоположный по знаку заряд, по сравнению с электроном. Таким образом, свободное от электрона квантовое состояние вблизи потолка валентной зоны и называют дыркой.
Важно отметить, что при переходах 1 à 2 à 3 … дырка приобретет кинетическую энергию, и полная энергия дырки возрастет (!!!), т.е. шкала энергий в валентной зоне возрастает в направлении – противоположном зоне проводимости.
Классический аналог увеличения энергии по зонам: взвешенная капля воды в воздухе (туман) – электрон в зоне проводимости, пузырек воздуха в воде – дырка в валентной зоне.
Таким образом, ток в кристаллах может переноситься не только электронами в зоне проводимости, но и дырками в валентной зоне. Дырочная проводимость наиболее характерна для полупроводников, однако есть и некоторые металлы, которые обладают дырочной проводимостью.
Возвращаясь к рис. 1.48в, отметим, что описывать движение электронов в кристалле, пользуясь понятием эффективной массы, можно только тогда, когда они находятся либо у дна, либо у потолка энергетической зоны. В центре зоны (около значений k = ± π/a) m*à∞, т.е. понятие эффективной массы теряет смысл. На практике почти всегда приходится иметь дело с электронами, располагающимися или у дна, или у потолка зоны. Поэтому использование эффективной массы в этих случаях вполне оправдано.
Ширина разрешенных зон растет, а запрещенных – уменьшается, с увеличением энергии (порядкового номера разрешенной зоны). Т.е. в общем случае зона проводимости, имеет большую ширину, чем валентная зона. Поскольку эффективная масса обратно пропорциональна ширине энергетической зоны, поэтому, как правило, 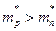 . Следовательно, дырка и электрон проводимости отличаются не только знаком своего заряда, но имеют и разные по величине m*.
. Следовательно, дырка и электрон проводимости отличаются не только знаком своего заряда, но имеют и разные по величине m*.
Иной результат получается, если в почти заполненной зоне имеются свободные места, то есть не все валентные связи обеспечены электронами. Тогда соседние электроны могут переходить на эти места, а само свободное место как бы перемещается в пространстве. В энергетическом плане это соответствует переходу электронов с низких энергетических уровней на более высокие, а дырок с высоких уровней на более низкие.
Резюмируя полученную информацию:
1. Обозначения носителей зарядов в полупроводнике.
| Электроны | n, e (negative, electrons) |
| Дырки | p, h (positive, holes) |
| Ток частично заполненной зоны может быть представлен как ток положительно заряженных частиц дырок. Заряд дырки положителен и по величине равен заряду электрона. Концентрация дырок обычно обозначается буквой р. |
2. Три представления (определения) дырок:
(a) полноправная положительно заряженная частица, перемещающая в кристалле.
(b) отсутствие электрона в потолке валентной зоны.
(c) физическое отсутствие электрона в том месте, где он должен быть в равновесном состоянии – т.е. в составе ковалентной связи.
3. Направление энергии в зонах: зона проводимости – энергия увеличивается вверх; валентная зона – энергия увеличивается вниз.
4. Величина m* зависит от кривизны зоны (m* ~ (d2E/dk2)-1)
5.Ширина зон увеличивается с E, а m* обратно пропорциональна ширине энергетической зоны, à (a) зона проводимости энергетически шире, чем валентная; (b)  (как правило).
(как правило).