Свойства математического ожидания

Сведения из теории интеграла.

Интеграл Стилтьеса.

Для дальнейшего изложения нам потребуется понятие интеграла Стилтьеса.

Пусть в интервале определены функция f(x) и неубывающая, непрерывная слева функция F(x). Разобьем интервал на непересекающиеся полуинтервалы и обозначим .

Возьмем произвольные точки и составим интегральную сумму вида:

Обозначим l_n максимальную из длин полуинтервалов разбиения.

Определение.Если при существует предел интегральных сумм S_n, не зависящий от последовательности точек деления интервала , то этот предел называется интегралом Стилтьеса от функции f(x) по функции F(x) по интервалу и обозначается .

Несобственный интеграл Стилтьеса, когда интервал интегрирования бесконечен, определяется обычным образом: рассматривается интеграл по конечному интервалу , границы интервала устремляются произвольным образом к бесконечности и если существует предел

то этот предел называется интегралом Стилтьеса от функции f(x) по функции F(x) в промежутке и обозначается .

Считается, что интеграл Стилтьеса от функции f(x) по функции F(x) существует тогда и только тогда, когда существует интеграл .

Если F(x) – функция распределения с.в., то

Если F(x) имеет производную p(x) и является интегралом от нее, то

Если F(x) кусочно-постоянная функция с разрывами в точках с₁,…с_n,… то

Интеграл Лебега.

Пусть F(x) – неубывающая функция, непрерывная слева. Эта функция порождает меру на прямой. Для интервала мера определяется в виде

С помощью предельного перехода мера может быть распространена на все борелевские множества.

Обратно, любая конечная мера (т.е мера, удовлетворяющая условию ) порождает неубывающая функцию, непрерывную слева

Определим понятие интеграла функции f(x) по мере m.

Определение.Пусть задана система непересекающихся борелевских множеств A_n, причем

. Пусть функция f(x) принимает постоянные значения на множествах A_n;

Тогда интегралом Лебега функции f(x) по мере m называется выражение

По условию этот интеграл определяется как конечное число в тех случаях, когда

Пусть функция f(x) принимает конечное или счетное множество значений f_i, причем множество тех x, для которых f(x)= f_i, является борелевским. Тогда f(x) назовем кусочно-постоянной функцией. Вышеприведенное определение интеграла Лебега дано для кусочно-постоянной функции. Обобщим его на случай произвольной функции.

Определение.Пусть f(x) – произвольная функция, а - последовательность кусочно-постоянных функций, равномерно сходящаяся к f(x). Тогда интегралом Лебега функции f(x) по мере m называется выражение

Моменты с.в.

Во многих практических задачах не нужно знать исчерпывающую характеристику с.в., такую как ее функция распределения, а достаточно знать лишь некоторые числовые характеристики, к которым относятся так называемые моменты с.в.

Определение. Моментом порядка k д.с.в. x, принимающей значения x_i с вероятностями р_i называется число

при условии, что указанный ряд сходится абсолютно, т.е.

Определение. Моментом порядка k н.с.в. x с плотностью распределения f_x(x) называется число

при условии, что указанный интеграл сходится абсолютно, т.е.

Величину принято называть абсолютным моментом порядка k. Если не существует, то говорят, что с.в. не имеет конечного момента порядка k. По определению, моменты 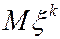и существуют или не существуют одновременно. Требование абсолютной сходимости гарантирует возможность произвольного порядка суммирования и, следовательно, корректность определения .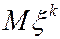

Замечание.

На основании введенных понятий интегралов Стилтьеса и Лебега, можно видеть, что приведенные выражения для 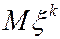являются частными случаями более общей записи:

Последние записи более удобны для общих выводов и позволяют не конкретизировать вид с.в., с которой мы работаем.

Определение. Момент Мx первого порядка называется математическим ожиданием или средним значением с.в. x.

Свойства математического ожидания

1. Мс=с.

3. Если с.в. - независимы, то .

Понятие независимости с.в. будет введено позднее, оно основывается на независимости событий, состоящих в принадлежности с.в. к произвольным борелевским множествам.

Примеры вычисления МО.

1. Биномиальное распределение

2. Равномерное распределение

- середина отрезка [a,b].

3. Определение. Математическое ожидание называется k–ым центральным моментом, если существует k–ый абсолютный центральный момент .

Определение. Центральный момент 2-го порядка называется дисперсией и обозначается .

Этот момент является удобной характеристикой разброса значений с.в. x около ее среднего значения:

Видно, что разброс вокруг средних у этих с.в. одинаков и дисперсии также одинаковы.

Свойства дисперсии

1. Dс=0.

4. Если с.в. - независимы, то .

12 Следующая ⇒