Главная | Обратная связь

Формула для вычисления дисперсии.

- средний квадрат минус квадрат среднего.

Число называется средним квадратическим отклонением случайной величины .

 

Примеры вычисления дисперсии.

1. Биномиальное распределение

 

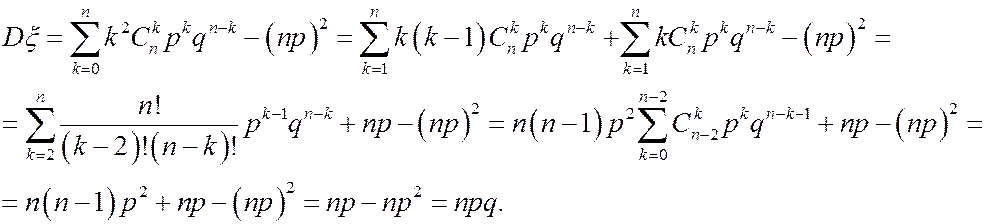
2. Равномерное распределение

 

Функции от случайных величин.

Во многих задачах дана какая либо с.в. x с функцией распределения F_x(x) и требуется найти характеристики с.в. .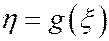

Рассмотрим эту задачу для некоторых частных случаев.

1) Пусть – монотонно-возрастающая, непрерывно-дифференцируемая функция, тогда .

Для д.с.в. формула для вероятностей преобразованной с.в. запишется в виде:

Для н.с.в. получим формулу преобразования плотности:

,

.

 

Воспользуемся формулой дифференцирования по параметру

и получим

.

2) Пусть – монотонно-убывающая, непрерывно-дифференцируемая функция, тогда .

Для д.с.в. формула преобразования закона распределения не изменится, а для н.с.в. будем иметь:

,

.

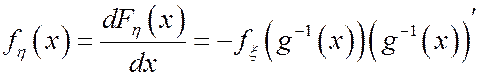Учитывая, что для монотонно-убывающей функции , а для монотонно-возрастающей функции , то случаи 1,2 можно объединить:

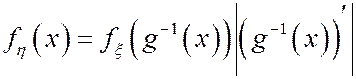
3) Пусть – кусочно-монотонная, непрерывно-дифференцируемая на интервалах монотонности функция. В этом случае ограничимся формулой для плотности.

Разобьем область определения на интервалы монотонности А_i, i=1,2,…n.

Каждый интервал А_i, функция переводит в интервал В_i. Используя полученную формулу для плотности, будем иметь:

,

где - функция, обратная к на интервале монотонности А_i.

 

Пример.

Пусть с.в. x имеет плотность f_x(x). Найти плотность с.в. .

Решение.

Интервалов монотонности два.

1) При и , .

2) При и , .

Т.О.,

 

Моменты функций от с.в. на примере МО.

Осталось рассмотреть задачу о вычислении моментов функций от с.в.

Теорема.

Пусть x - дискретная (непрерывная) с.в., принимающая значения x₁,x₂,… с вероятностями р₁,р₂,… (имеющая плотность вероятности f_x(x)), а 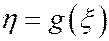- новая случайная величина, где g – некоторая функция. Тогда МО с.в. 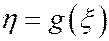равно:

,

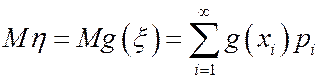
если этот ряд (интеграл) сходится абсолютно.

Доказательство.

1)Докажем формулу для случая д.с.в.

Возможными значениями с.в. 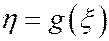будут числа

Вероятность любого из этих значений находится по формуле .

По определению МО будем иметь

2) Идея доказательства для случая н.с.в.

Введем с.в. , называемую e-приближением к с.в. 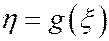. С.В. принимает дискретный ряд значений с вероятностями .

Величина получается путем округления значений, принимаемых с.в. , до ближайших слева точек e-сети, состоящей из точек оси Ох. При этом .

Обозначим 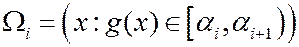, тогда

 

 

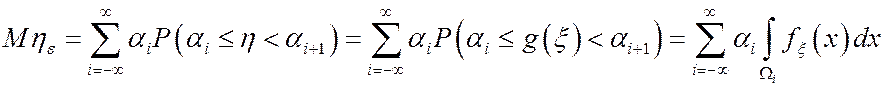
Рассмотрим разность

При (в том смысле, что согласно построению с.в. ), а .

Т.О., для моментов функций от с.в. необязательно искать сначала новую плотность или закон распределения, можно воспользоваться формулами из теоремы, которые легко обобщаются на случай других моментов.

Например,

, .