 |
|
Действия над случайными величинами.
Пример.
Пусть 
.
Рассмотрим с.в. x и |x|.
Если x>0, то x|x|=x2, а если x<0, то x|x|=-x2, поэтому 
.
Т.О. Rx|x|=0, но с.в. x и |x| не являются независимыми, поскольку одна из них полностью определяет другую.
Значение Rxh зависит от масштаба величин x,h. Поэтому удобно характеризовать связь между с.в. коэффициентом корреляции, который определяется как 
.
Свойства коэффициента корреляции.
1. Если с.в. x,h - независимы, то rxh=0.
2. | rxh|<=1
3. | rxh|=1 Û x=ah+b
Свойство 1 очевидно, докажем свойства 2,3.
Доказательство свойства 2.
Для любого с
Положим 
, тогда
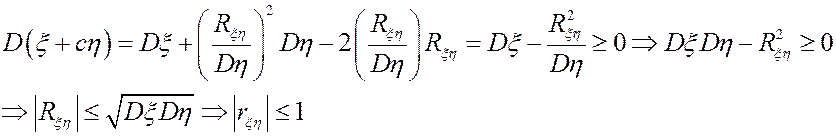
Доказательство свойства 3.
Необходимость (считаем, что | rxh|=1)
Пусть 
.
Рассмотрим
При | rxh|=1 rxh=±1. При rxh=+1 выбираем «-», а при rxh=+1 выбираем «+» в выражении под дисперсией и получаем, что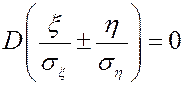 
. Если дисперсия равна нулю, то с.в. есть константа, то есть 
.
Достаточность доказывается непосредственным расчетом.
Определение. С.в. x,h называются некоррелированными, если Rxh=0 (или rxh=0).
Замечание. Некоррелированность, как мы видели, не влечет независимость. Но есть один вид с.в., для которого это верно. Если две нормальные (гауссовские) с.в. некоррелированы, то они независимы.
Определение. Для случайного вектора 
матрица R=| Rij|i,j=1,…,n, где Rij=Rxixj
называется корреляционной матрицей случайного вектора .
Заметим, что Rij=Dxi, Rij=Rij, то есть матрица симметричная, а диагональные элементы соответствуют дисперсиям.
Свойство матрицы R: корреляционная матрица является положительно-определенной.
Доказательство.
имеем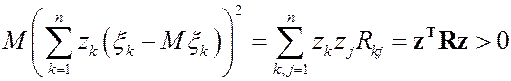 
.
Условные моменты случайных величин.
Определение. Условным МО с.в. x при условии h=y, где h - другая с.в., называется
.
Напомним, что 
Для д.с.в. 
Для н.с.в.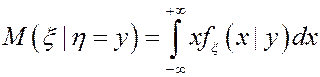 
Получим формулы для связи условных моментов с безусловными.
Пусть 
– непересекающиеся интервалы, 
, тогда, по ф.п.в.
.
Итак, 
Для н.с.в. 
Для д.с.в. 
Полученные формулы можно представить в виде 
Пример.
Рабочий обслуживает n однотипных станков, расположенных вдоль прямой на расстоянии а один от другого.
Считаем, что рабочий может находиться у любого станка с вероятностью1/n. Будем считать, что с вероятностью 1/n любой станок может потребовать внимания рабочего и рабочий пойдет к нему. Найти МО величины перехода.
Решение.
Пронумеруем станки числами от 1 до n слева направо.
Пусть h– с.в., которая обозначает, что рабочий находится у определенного станка, h= 1,…,n, P(h=i)=1/n. Пусть рабочий находится у станка с номером k и пусть потребовал внимания станок с номером i, тогда величина перехода
(*).
Т.О., величина перехода есть с.в. x, принимающая значения (*) при i=1,…,n с вероятностями 1/n.
Воспользуемся формулой .
При получении вышеприведенного выражения мы воспользовались формулой для суммы арифметической прогрессии 
.
Воспользовавшись формулой 
, последнее выражение можно преобразовать к виду:
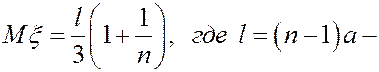расстояние между крайними станками.
Действия над случайными величинами.
Формулы для моментов сумм, произведений двух или более с.в. несложно получить зная плотность результирующей с.в., равной функции от исходных с.в. Поэтому мы рассмотрим формулы для функций распределения и плотностей сумм с.в., произведений с.в., и.т.д.
Сумма двух с.в.
Пусть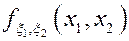 
- двумерная плотность с.в. (x1,x2). Рассмотрим с.в. x=x1+x2.
Найдем 
.
Рассматривая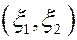 
как декартовы координаты 
, мы должны определить вид области D, для которой 
. Тогда
Т.О. 
Для независимых с.в. 
- свертка плотностей и
Задача 1.
(x1,x2) – независимые экспоненциальные с.в.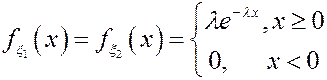 
Найти 
.
Ответ: 
Частное двух с.в.
Найдем функцию распределения частного двух с.в. 
.
Пусть z>0. Рассматривая 
как декартовы координаты (x,y), мы должны определить вид области, для которой x/y<z, z>0.
Во первых, область включает 2-ой и 4-ый квадранты, где x/y<0 и, следовательно меньше z. В первом квадранте x>0,y>0, поэтому y>x/z. В третьем квадранте x<0,y<0, поэтому y<x/z.
Продифференцировав по z, найдем
Если исходные с.в. независимы, то
Повторив вычисления для z<0, можно видеть, что плотность будет такой же, как и полученная выше.