Результаты группировки

Задание

На основании данных статистического наблюдения (провести самостоятельно, должно быть не менее 50 единиц наблюдения) произвести группировку с равными интервалами. Результаты группировки оформить в виде таблицы, а также представить графически с помощью:

a) гистограммы;

b) кумуляты.

Рассчитать среднее значение исследуемого показателя, моду, медиану полученного ряда распределения. Охарактеризовать характер распределения и степень вариации признака, положенного в основание группировки. Сделать выводы.

Темы для изучения при выполнении КР: статистическое наблюдение; сводка и группировка данных статистического наблюдения; средние величины; показатели вариации.

Исходные данные

Сняты экспериментальные данные операции контроля, характеризующие активную пористость сложных керамических систем (бетон) при толщине изделия 250 мм и постоянной структуре.

Таблица № 1

Исходные данные

№ опыта	Пористость, %	№ опыта	Пористость, %
	17,35		22,14
	17,84		15,06
	19,62		17,03
	17,65		18,19
	18,02
	17,34		16,16
	16,78		18,79
	19,14		19,01
	15,42		18,72
	21,75		15,89
	17,01		17,46
	16,88		16,13
	19,01		15,76
	20,74		18,46
	18,06		16,97
	21,24		19,68
	19,76		15,06
	20,44		20,16
	16,02		19,48
	22,07		22,05
	17,12		20,38
	18,61		16,05
	19,45		20,68
	21,89		16,56
	17,06		20,19

Сводка и группировка данных статистического наблюдения. Определение средних величин и показателей вариации

1. Произведем группировку с равными интервалами.

Определим число групп математическим путем с использованием формулы Стерджесса:

n = 1+3,322 lg N = 1+3,322 lg 50 = 6,644 = 7

где n – число групп; N – число единиц совокупности.

Определим величину интервала в случае группировки с равными интервалами:

h = ;

где Х_max, Х_min – максимальное и минимальное значение признака в совокупности; n – число групп.

Частота — количество элементов совокупности, которые имеют данное значение признака.

Частость — отношение частоты к общему количеству исследуемых элементов, т.е. объему совокупности.

Результаты группировки представлены в таблице № 2.

Таблица № 2

Результаты группировки

№ группы	№ опыта	Пористость, %	№ опыта	Пористость, %	Частота повторения	Накопленная частота	Среднее значение интервала	Частости, %
15,06 – 16,07		15,42		15,76			15,565
	16,02		15,06
	15,06		16,05
	15,89
16,08 – 17,09		16,78		16,16			16,585
	17,01		16,13
	16,88		16,97
	17,06		16,56
	17,03
17,10 – 18,11		17,35		17,65			17,605
	17,84		18,02
	17,12		17,34
	17,46		18,06
18,12 –19,13		19,01		18,79			18,625
	18,61		19,01
	18,19		18,72
	18,46
19,14 –20,15		19,62					19,645
	19,14		19,68
	19,76		19,48
	19,45
20,16 –21,17		20,74		20,38			20,665
	20,44		20,68
	20,16		20,19
21,18 –22,19		21,24		21,24			21,685
	21,89		21,89
	22,14		22,14

Построим гистограмму (рис. 1) и кумуляту (рис. 2), огиву (рис. 3) распределения.

Гистограмма, это способ представления статистических данных в графическом виде – в виде столбчатой диаграммы. Она отображает распределение отдельных измерений параметров изделия или процесса.

Рис. 1. Гистограмма частот

Кумулята — ломаная кривая, строящаяся на основе прямоугольной системы координат, когда по оси X откладываются значения признака, а по оси Y — накопленные частоты.

Рис. 2. Кумулята

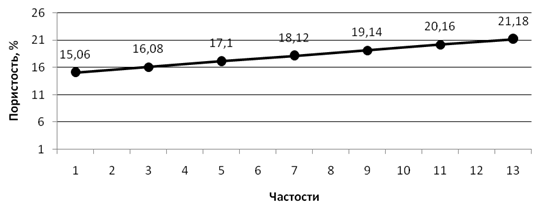
Рис. 3. Огива

2. Рассчитаем среднее значение исследуемого показателя, моду, медиану полученного ряда распределения.

Для данных, представленных в виде интервального ряда распределения, среднее значение показателя рассчитывается по формуле средней арифметической взвешенной:

где X_i – срединное значение интервала; ƒi – частота интервала.

Рассчитаем моду интервального вариационного ряда.

Модальный интервал — это интервал, который имеет наибольшую частоту.

Модальный интервал – 2 группа: 16,08 – 17,09.

где Х_мо- нижняя граница модального интервала; i_мо – величина модального интервала; f_мо – частота модального интервала; f_мо-1 – частота интервала, предшествующего модальному; f_мо+1– частота интервала, следующего за модальным.

Рассчитаем медиану интервального вариационного ряда.

Медианный интервал — это интервал, в котором сумма накопленных частот составляет половину или больше половины всей суммы частот ряда. Медианный интервал – 4 группа: 18,12 –19,13.

где Х_ме – нижняя граница значения интервала, содержащего медиану; i_ме – величина медианного интервала; Σf – сумма частот ряда распределения; S_ме-1 – сумма накопленных частот, предшествующих медианному интервалу; ƒ_ме– частота медианного интервала.

3. Охарактеризуем вариацию изучаемого признака с помощью абсолютных, средних и относительных показателей вариации.

Размах вариации (R)

R = X_max – X_min = 22,14 – 15,06 = 7,08 %,

где X_max – наибольшее значение варьирующего признака; X_min – наименьшее значение признака.

Среднее линейное отклонение представляет собой среднюю величину из отклонений вариантов признака от их средней.

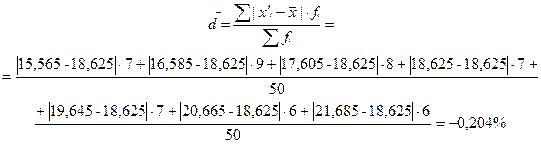где n – число единиц наблюдения; f_i– частота интервала; x`_i – среднее значение в интервале вариационного ряда; - общая средняя ряда

Дисперсия - представляет собой средний квадрат отклонений индивидуальный значений признака от их средней величины.

Среднее квадратическое отклонение представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от из средней:

Коэффициент осцилляции

характеризует отклонение крайних значений признака от среднего значения.

Относительное линейное отклонение

характеризует отклонение среднего линейного отклонения от средней.

Коэффициент вариации

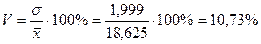
Так как V<33 %, то статистическая совокупность является однородной, т.е. средняя объективна.

4. Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и оценку его симметричности, остро- или плосковершинности. Симметричным называется распределение, в котором частоты любых двух вариант, равноотстоящих в обе стороны от центра распределения равны между собой. В статистике для характеристики асимметрии пользуются следующими показателями.

Коэффициент асимметрии

A_S = ,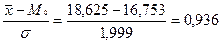

где - средняя арифметическая ряда распределения; М₀ – мода; - среднее квадратическое отклонение.

Так как A_S > 0, то больше моды, т.е. имеется правосторонняя асимметрия.

Для симметричных распределений может быть рассчитан коэффициент эксцесса, который показывает, насколько резкий скачок имеет изучаемое явление. Если коэффициент эксцесса больше нуля, то распределение островершинное и скачок считается значительным, если коэффициент эксцесса меньше нуля, то распределение считается плосковершинным и скачок считается незначительным.

Коэффициент эксцесса

Е_К =

Где М₄ – четвертая величина центрального момента

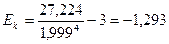
Заключение

Исследовав выборочную совокупность результатов проведения промежуточного контроля свойств бетона с водоцементным отношением В/Ц 0,8 на контрольной операции технологического процесса изготовления железобетонных плит на ОАО «Завод железобетонных изделий» г.Владимир, взяв в качестве группировочного признака величину пористости и построив интервальный вариационный ряд из 7 групп можно сделать следующие выводы:

– средняя арифметическая взвешенная пористости бетона составила 18,421% от общего объема материала;

– самым распространенным значением параметра пористости является 16,753%, то есть ниже среднего (определено модой) и говорит о высоком качестве производимой продукции, так как допустимое значение пористости для бетонного камня с данными характеристиками не должно превышать 23%;

– половина изделий имеют значения пористости более чем 18,26 %, а половина – меньше данной величины (определено медианой);

– самое высокое значение пористости бетонной плиты на 7,08% больше самого низкого значения пористости (определено размахом вариации), данный размах обусловлен неоднородным процессом формирования гелевой структуры в бетонном камне;

– построенный ряд распределения является однородным, следовательно средняя ряда объективна (определено коэффициентом вариации);

– распределение ряда ассиметрично, имеется правосторонняя ассиметрия (определено коэффициентом ассиметрии);

– распределение является плосковершинным (определено коэффициентом эксцесса).

Список литературы

1. Общая теория статистики. Под ред. А.А. Спирина, О.Э. Башиной М: «Финансы и статистика», 1976 г.

2. Малый И.Г. и др. Теория статистики: Учебник. М: «Финансы и статистика», 1984 г.

3. Общая теория статистики: Учебник (Т.В. Рябушкин, М.Р. Ефимова, И.М. Игнатова, НИ Яковлева), М: «Финансы и статистика», 1988 г.

4. Р.А. Шмойлова, В.Г. Минашкин, Н.А. Садовникова. Практикум по теории статистики.М: «Финансы и статистика», 2007 г.

5. Лаврищева Е.Е. Статистика: учебно-методическое пособие/ Е.Е. Лаврищева, С. Ю. Космачев. – Ковров: ГОУ ВПО «КГТА им. В.А. Дегтярева», 2009. – 104 с.

6. Лаврищева Е.Е. Методические указания к выполнению домашних заданий/ Сост. Е.Е. Лаврищева. – Ковров: КГТА, 2001. – 28 с.