 |
|
Необходимые сведения из теории вероятностей, математической статистики и теории информации
 - элементарное случайное событие,
- элементарное случайное событие,
 - пространство элементарных событий.
- пространство элементарных событий.
 ,
,  ,
,
 - событие
- событие  считается невозможным,
считается невозможным,
 - событие
- событие  считается достоверным.
считается достоверным.
 , где
, где  - число попаданий в i-ую ячейку, а N - число выстрелов по мишени.
- число попаданий в i-ую ячейку, а N - число выстрелов по мишени.
 ,
,
условие нормировки:  .
.
Выделим на мишени два сектора: a и b
 4 4
| |||
 b a
b a
А - попадание в сектор a = {6,10,14},
В - попадание в сектор b = {10,11,12}.
 ,
,
 .
.
Объединение или сумма событий:  или А+В.
или А+В.
Пересечение или произведение событий: 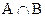 или
или  .
.
Если  , то события A и В называются несовместными.
, то события A и В называются несовместными.
Событие А+В – это попадание в сектор 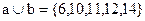 .
.
Событие  – попадание в сектор
– попадание в сектор  .
.
 , и
, и
 , то есть
, то есть
 – формула сложения вероятностей.
– формула сложения вероятностей.
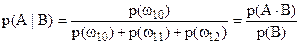 , следовательно
, следовательно
 – формула умножения вероятностей.
– формула умножения вероятностей.
События A и B называют независимыми, если  ,
,  .
.
 ,
, 
 – формула Байеса.
– формула Байеса.
Выделим в мишени четыре сектора:  ,
,  ,
,  и b.
и b.  Ø и
Ø и  .
.



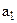


 4 4
| |||
b
Поскольку
 ,
,  ,
,
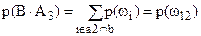 , то
, то
 и
и
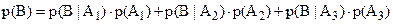 – формула полной вероятности.
– формула полной вероятности.
 , в нашем примере
, в нашем примере  .
.
Обозначения: X – СВ,  – i-ое значение СВ,
– i-ое значение СВ,  – вероятность значения СВ
– вероятность значения СВ  . Условие нормировки:
. Условие нормировки:  .
.
| X | 
| 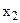
| … | 
|

| 
| 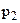
| … | 
|
Функция распределения :  .
.
Основные числовые характеристики дискретной СВ:
математическое ожидание:  ;
;
дисперсия: 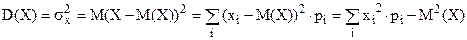 ;
;
среднее квадратическое отклонение(СКО) : 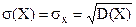 .
.
Пр.
| X | ||||

| 0,1 | 0,5 | 0,3 | 0,1 |
 ;
;  ;
; 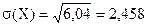 .
.
Пплотность вероятности f(x) (плотность распределения вероятностей):
 Условие нормировки:
Условие нормировки:  .
.

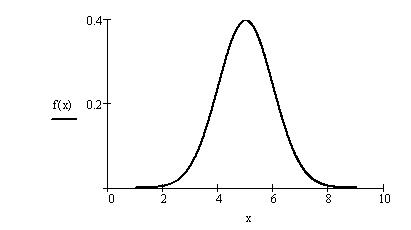
Основные свойства плотности вероятности:
 ,
,  ,
,  .
.
Основные числовые характеристики непрерывной СВ:
математическое ожидание:  ;
;
дисперсия:  ;
;
среднее квадратическое отклонение(СКО) : 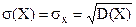 .
.
ковариация: cov(X,Y) =  ;
;
коэффициент корреляции:  .
.
Свойства коэффициента корреляции:
 ;
; 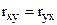 ;
;  ;
;
если СВ X и Y независимы, то  ;
;
 тогда и только тогда, когда
тогда и только тогда, когда  , a,b = const.
, a,b = const.
 ,
,
 ,
,
где  – шаг разбиения.
– шаг разбиения.
Пусть N – объем выборки, а 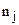 – количество значений СВ, попавших в j-ый подынтервал, тогда интервальный статистический рядбудет иметь вид:
– количество значений СВ, попавших в j-ый подынтервал, тогда интервальный статистический рядбудет иметь вид:

| 
| … | 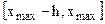
|

| 
| … | 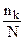
|
 - высота прямоугольников
- высота прямоугольников

 - выборка,
- выборка,
 - характеристика СВ,
- характеристика СВ,
 - оценка характеристики
- оценка характеристики  СВ.
СВ.
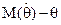 - смещение или систематическая ошибка оценивания.
- смещение или систематическая ошибка оценивания.
Оценка  называется несмещенной, если
называется несмещенной, если  , т.е.
, т.е.  .
.
Оценка  называется эффективной, если
называется эффективной, если  , где
, где  – любая другая оценка параметра
– любая другая оценка параметра  .
.
Оценка  называется асимптотически эффективной, если
называется асимптотически эффективной, если  при
при  (индекс N в оценке – для обозначения объема выборки).
(индекс N в оценке – для обозначения объема выборки).
Оценка  называется состоятельной, если
называется состоятельной, если  при
при  .
.
Справедливо следующее утверждение: если  и
и  при
при  , то
, то  – состоятельная оценка параметра
– состоятельная оценка параметра  .
.
Выборочное среднее:  ;
;
выборочная дисперсия:  ;
;
несмещенная и состоятельная оценка дисперсии:  ;
;
несмещенная и состоятельная оценка СКО: 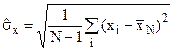 ;
;
несмещенные и состоятельные оценки ковариации и коэффициента корреляции
двух СВ - X и Y: 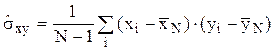 ,
, 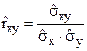 .
.
Пусть возможные исходы эксперимента - события 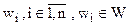 , а
, а  - сообщение о наступлении i-го события.
- сообщение о наступлении i-го события.


Формула Шеннона:  .
.
 - энтропия вероятностного эксперимента.
- энтропия вероятностного эксперимента.
 Пр. 1. Пусть эксперимент имеет два исхода:
Пр. 1. Пусть эксперимент имеет два исхода:  . Соответствующие их вероятности:
. Соответствующие их вероятности:  .Тогда
.Тогда  . Наибольшая энтропия, т.е. неопределенность относительно исхода эксперимента имеется при равновероятных исходах: I = max = 1, если
. Наибольшая энтропия, т.е. неопределенность относительно исхода эксперимента имеется при равновероятных исходах: I = max = 1, если  .
.
2. Пусть имеется множество объектов Q, включающее в себя объекты k разных
видов, а  ,
,  – количество объектов i-го вида в множестве Q. Т.е.
– количество объектов i-го вида в множестве Q. Т.е.
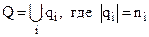 и
и  Ø для
Ø для 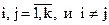 . Тогда вероятность того, что выбранный наугад объект из Q окажется объектом i-го вида равна
. Тогда вероятность того, что выбранный наугад объект из Q окажется объектом i-го вида равна  и, следовательно, энтропия выбора объекта в этом случае будет такой:
и, следовательно, энтропия выбора объекта в этом случае будет такой:
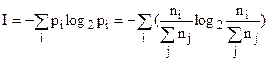 .
.