 |
|
Дії над комплексними числами в тригонометричній формі.
Форми запису (форми представлення) комплексного числа.
Тригонометрична форма запису.
Геометричне зображення комплексного числа.
Комплексне число  геометрично зображують точкою
геометрично зображують точкою  координатної площини.
координатної площини.

Зручно комплексне число зобразити у вигляді вектора
 .
.
Довжина вектора, який зображає комплексне число, називається модулем цього комплексного числа. Модуль комплексного числа позначається  . Тобто
. Тобто
 . (1)
. (1)
Кут 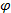 між додатним напрямком осі абсцис і вектором
між додатним напрямком осі абсцис і вектором  називається аргументом комплексного числа.
називається аргументом комплексного числа.
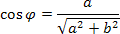 (2)
(2)
 (3)
(3)

Примітка! Кожне комплексне число, що не дорівнює нулю, має нескінчену множину аргументів, які відрізняються один від одного на  , де
, де  – ціле число, тобто у якості аргументу можна обирати будь яке значення
– ціле число, тобто у якості аргументу можна обирати будь яке значення  .
.
Для однозначного визначення аргументу комплексного числа будемо обирати його з певного проміжку довжиною 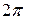 . Таке значення аргументу називається його головним значенням та позначається
. Таке значення аргументу називається його головним значенням та позначається  . Будемо вважати, що
. Будемо вважати, що  належить проміжку
належить проміжку  ). Тоді модуль та головне значення аргументу комплексного числа доцільно обчислювати за формулами
). Тоді модуль та головне значення аргументу комплексного числа доцільно обчислювати за формулами
 ;
;
 . (4)
. (4)
Приклад.Знайти модуль та аргумент числа  .
.
Розв’язок: за умовою  ,
,  .
.
За формулою (1) маємо:  .
.
За формулою (4), оскільки 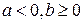 :
:
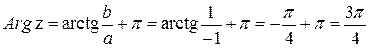 .
.
Тригонометрична форма комплексного числа.
Виразивши  і
і  через модуль
через модуль  і аргумент
і аргумент 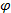 , комплексне число
, комплексне число  запишемо у вигляді
запишемо у вигляді
 (5)
(5)
Права частина цієї тотожності називається тригонометричною формою комплексного числа.
Доведення. З урахуванням (1), (2) і (3), отримаємо:

Почленно помноживши дужку на  і скоротивши, маємо:
і скоротивши, маємо:

Приклад.Знайти модуль та аргумент числа  .
.
Розв’язок: за умовою  ,
,  .
.
Знайдемо модуль  та аргумент
та аргумент 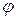 числа
числа 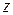 :
:
1) за формулою (1) маємо:  .
.
2) за формулою (4), оскільки  :
:  .
.
Отже, тригонометрична форма запису:
 .
.
Дії над комплексними числами в тригонометричній формі.
Нехай задано два комплексні числа:
 ,
,  .
.
1. Множення
 .
.
Тобто при множенні комплексних чисел в тригонометричній формі потрібно перемножити їх модулі 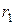 і
і  , а аргументи
, а аргументи 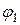 і
і  скласти.
скласти.
Приклад (множення комплексних чисел в тригонометричній формі):
Помножити два числа  і
і  .
.
Розв’язання: 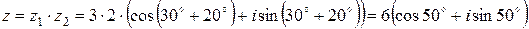 .
.
2. Ділення
 .
.
Тобто при діленні комплексних чисел в тригонометричній формі потрібно поділити їх модулі 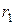 і
і  , а аргументи
, а аргументи 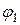 і
і  відняти.
відняти.
Приклад (ділення комплексних чисел в тригонометричній формі):
Поділити два числа  і
і  .
.
Розв’язання:  .
.
З урахуванням того, що функція  є парною, а
є парною, а  є непарною, отримаємо:
є непарною, отримаємо: 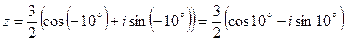 .
.
3. Піднесення до степеня(формула Муавра)
 .
.
Тобто при піднесенні до степеня комплексних чисел в тригонометричній формі потрібно піднести до цього степеня його модуль  , а аргумент
, а аргумент 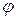 помножити на цей степінь.
помножити на цей степінь.
Приклад (піднесення до степеня комплексних чисел в тригонометричній формі):
Піднести до другого та п’ятого степенів число  .
.
Розв’язок:  ,
,
 .
.
4. Добування кореня
 , (6)
, (6)
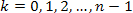 .
.
Тобто матимемо  різних значень кореня.
різних значень кореня.
Приклад (добування кореня):
Знайти корені 3-го степеня з числа  .
.
Розв’язок: згідно з формулою (6) будемо мати 3 кореня:
1) при  :
: 
2) при  :
: 
3) при  :
: 
Зауваження. Таким чином, ми бачимо, що розглянуті 4 операції дуже легко виконуються над комплексними числами, записаними в тригонометричній формі, в той час, як лише перші дві з них (множення та ділення) зручно виконувати і для чисел, записаних в алгебраїчній формі. Тому для здійснення операцій піднесення до степеня та добування кореня  -го степеня доцільно спочатку записати комплексне число в тригонометричній формі (якщо воно задане в алгебраїчній формі), а потім вже виконувати вказані операції.
-го степеня доцільно спочатку записати комплексне число в тригонометричній формі (якщо воно задане в алгебраїчній формі), а потім вже виконувати вказані операції.
Завдання для самоконтролю.
1. Запишіть числа в тригонометричній формі: 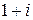 ;
;  .
.
2. Знайдіть добуток та частку двох комплексних чисел в тригонометричній формі з першого завдання (процес розв’язку розписати докладно).
1. Піднести число  до 3-го степеня, а
до 3-го степеня, а  – до сьомого.
– до сьомого.
2. Знайти корені 4-го степеня з першого комплексного числа в першому завданні.
Відповіді:
1.  ;
;  .
.
2. 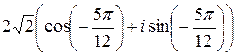 ;
; 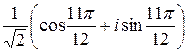 .
.
3.  ;
;  .
.
4.  ,
,  ,
,  ,
, 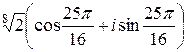 .
.