 |
|
Действия над комплексными числами в алгебраической форме.
Комплексные числа.
В арифметике и алгебре рассматривают различные действия над числами: арифметические (сложение, вычитание, умножение, деление), возведение в степень, извлечение корня и т.д. Только два действия – сложение и умножение – безусловно, выполнимы в области натуральных чисел: сумма и произведение натуральных чисел - также натуральные числа. Однако в области арифметики натуральных чисел уже вычитание не всегда выполнимо – для возможности образования разности двух натуральных чисел множество 
нужно дополнить до множества целых чисел 
, введя в него ноль и целые отрицательные числа. Такие операции как деление и извлечение корня становятся выполнимыми только после расширения рассматриваемой числовой области: множество целых чисел должно быть, соответственно, дополнено вначале до множества 
за счет введения рациональных чисел, а потом и до множества действительных чисел 
за счет введения иррациональных чисел.
Этот процесс можно схематически изобразить цепочкой 
, где , , , обозначают соответственно множества натуральных, целых, рациональных и действительных чисел. Причем каждая последующая числовая система сохраняет все основные свойства предыдущей и обладает рядом новых полезных свойств. Так, в можно только складывать и умножать, в можно уже вычитать, в ‑ делить. Во множестве действительных чисел можно извлекать корни любой степени из положительных чисел, хотя в даже число 
не имеет смысла. Но и во множестве действительных чисел такое простое уравнение 
не имеет решений. Так как многие задачи практики приводят к алгебраическим уравнениям, требуется построить новое множество, содержащее множество действительных чисел и решение любого алгебраического уравнения.
Комплексными числами называются числа вида a+bi , где a и b – действительные числа, а число i, определяемое равенством i2 =-1, называется мнимой единицей. Число a называется действительной частью комплексного числа и обозначается ReZ, b – мнимой частью комплексного числа и обозначается ImZ.
Пример 1. Найти 
и 
если: а) 
б) 
в) 
Решение. а) Так как 
то 
; б) Поскольку 
то 
; в) Запишем число в стандартном виде: 
Поэтому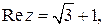 
Если a=0, то комплексное число bi называется чисто мнимым. Если b=0, то комплексное число a+bi равно a и называется действительным. Если a=0 и b=0 одновременно, то комплексное число 0+0i равно нулю.
Два комплексных числа a+bi и c+di называются равными тогда и только тогда, когда в отдельности равны их действительные и мнимые части, т.е.a=c, b=d.
Комплексные числа вида a+bi и -a-bi называются противоположными.
Комплексное число a+bi называется комплексно сопряжённым с числом a-bi и означается 
----------------------------------------------------------------------------------------------------------------
Комплексные числа. Стр.1
Запись комплексного числа в виде Z= a+bi называется алгебраической формой комплексного числа.
Множество всех комплексных чисел обозначают . Имеет место: 
.
Действия над комплексными числами в алгебраической форме.
Над комплексными числами, записанными в алгебраической форме, можно осуществлять все алгебраические операции как над обычными двучленами, учитывая лишь, что i2 =-1.
1) Сложение:(a+bi)+(c+di)=(a+c)+(b+d)i.
2) Вычитание:(а+bi)-(c+di)=(a-c)+(b-d)i.
3) Умножение: (a+bi)(c+di)=ac+bci+adi+bdi2=(ac-bd)+(ad+bc)i.
4) Деление: при делении комплексных чисел числитель и знаменатель дроби домножают на число, сопряжённое к знаменателю дроби.
Пример 2.Даны комплексные числа 
и 
Найти:
а) 
б) 
в) 
г) 
Решение. а) 
б) 
в) 
г) Для нахождения частного 
умножим числитель и знаменатель дроби на 
(т. е. на число, сопряженное знаменателю). Тогда получим
