 |
|
Размерность линейного пространства.
Лекция 2. ПОДПРОСТРАНСТВА
2.1. Размерность линейного пространства.
2.2. Подпространства линейного пространства.
2.3. Линейные оболочки. Изоморфизм линейных пространств.
Размерность линейного пространства.
Определение. Если в линейном пространстве 
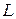существует линейно независимая совокупность из 
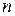векторов, а всякие 
вектор линейно зависимы, то это пространство 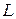называется 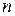-мерным.
Если в линейном пространстве имеется любое количество линейно независимых векторов, то оно называется бесконечно мерным.
Теорема. а) Если линейное пространство 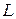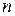-мерно, то в нем существует базис из 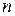векторов. б) Если в линейном пространстве 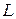существует базис из 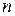векторов, то это пространство 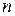-мерно.
Доказательство.
а) Дано: 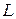– 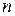-мерно, т.е. есть совокупность 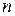линейно независимых векторов 
, а всякие вектор из 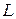– линейно зависимы. Присоединим к 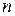векторам 
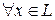. Эта совокупность векторов уже линейно зависима, поэтому из равенства нулю их линейной комбинации 
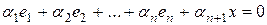следует, что хотя бы один из ее коэффициентов отличен от нуля. При этом единственной возможностью будет 
. При 
прийдем в противоречие с линейной независимостью векторов 
. Отсюда получаем:
.
Т.е. любой вектор 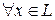линейно выражается через 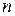векторов . Следовательно, они являются базисом.
Если пространство 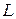– 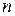-мерно, то базисом в нем будет любая совокупность 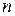линейно независимых векторов.
б) Дано: в 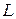есть базис из 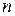векторов . Докажем, что любые вектор в 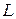образуют линейно зависимую совокупность. Надо доказать, что для любых : 
справедливо:
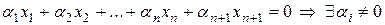. (2.1)
Разложим все эти векторы в базисе:
,
,
……………………………….
,
Подставим эти разложения в равенство (2.1). При этом получим:
(2.2)
Из линейной независимости векторов следует равенство нулю всех 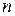коэффициентов в линейной комбинации (2.2):
(2.3)
Это система 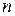линейных однородных алгебраических уравнений для определения коэффициента, которые введены в равенстве (2.1).
Ранг матрицы системы уравнений (2.3) меньше числа неизвестных, поэтому она имеет ненулевое решение. Для соотношения (2.1) это означает, что существует ненулевая линейная комбинация, равная нулю, т.е. любые 
линейно зависимы и векторное пространство 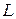– 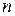-мерно.
Примеры:
1. Пространство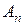 
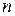-мерно, т.к. в нем есть базис из 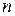векторов: 
; 
;…; 
.
2. В трехмерном пространстве свободных векторов есть базис из любых трех некомпланарных векторов.
3. В пространстве многочленов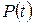 
степени 
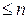базисом является линейно независимая совокупность из вектора: 1, 
, 
,…, 
. Размерность этого пространства равна .
Базис, вообще говоря, выбирается неоднозначно, но количество векторов в базисе равно размерности пространства.
4. В пространстве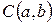 
функций непрерывных на сегменте 
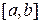базисные векторы 1, , ,…, ,…; их бесконечное число. Это бесконечномерное пространство, поэтому базиса в смысле, определенном ранее, здесь нет.